ABSTRACT
Effective personalization of education requires knowing how each student will perform under certain conditions, given their specific characteristics. Thus, the demand for interpretable and precise estimation of heterogeneous treatment effects is ever-present. This paper outlines a new approach to this problem based on the Leave-One-Out Potential Outcomes (LOOP) Estimator, which unbiasedly estimates individual treatment effects (ITE) from experiments. By regressing these estimates on a set of moderators, we obtain parameterized and easily interpretable estimates of conditional average treatment effects (CATE) that allow us to understand which individuals will likely benefit from each condition. We implement this approach with real-world data from an efficacy study that included four experimental conditions for instructing middle-school algebra. Our models indicate that treatment effect heterogeneity is significantly associated with students’ prior subject knowledge and whether English is their native language. We then discuss possibilities for applications to enhance personalized assignments.
Keywords
1. INTRODUCTION
Personalization – or giving each student exactly what they need to thrive – is a perennial goal for those working on Computer-Based Learning Platforms (CBLPs) [3]. The idea that CBLPs can be tailored to each student’s needs, thus mimicking the behaviors of responsive human tutors, has been a pursuit of many in the Education Data Mining (EDM) and related communities. Popular approaches often involve creating response features and algorithms that understand learners’ abilities and respond to their needs [24, 20, 11]. On the other hand, personalized program assignments can ensure that students receive the best possible instructional program to maximize their learning benefit. Either way, personalization may also be viewed as an issue of treatment effect heterogeneity – which occurs when the effect of a treatment differs for individuals based on some covariate(s). For example, a CBLP’s effect may vary based on students’ prior knowledge of the content. Similarly, a feature’s impact within a CBLP may vary based on students’ feelings toward the content. Thoroughly comprehending such variations will help inform personalized learning decisions like program assignments within learning systems.
Yet current methods of effect heterogeneity estimation can be too inflexible or difficult to interpret, especially when we want to understand how multiple dimensions of students’ characteristics may influence how they are affected by a particular educational experience. In the current study, we address this problem by combining two methods: Remnant-Based Leave-One-Out Potential Outcomes (ReLOOP) Estimator [15, 31] and Leave-One-Out Learner (LOOL), which we are proposing. ReLOOP provides individual effect estimates, and LOOL evaluates how those effects vary based on students’ characteristics. We apply this method to data from an experiment that evaluated three CBLPs with different approaches to teaching algebra concepts to U.S. middle school students. We find that LOOL identifies student characteristics that explain the variance in the effectiveness of these programs and discuss implications for personalization.
2. BACKGROUND
2.1 Effect Heterogeneity in Education
Understanding who benefits from which educational program has long been a goal of education research [32, 7, 41, 14]. Recent qualitative work on intersectionality – the idea that people have overlapping identities that influence their experiences – has pushed researchers to think more critically about how individuals may experience and benefit from educational programs and policies differently [33]. In the context of educational technologies and algorithmic bias, Kizilcec & Lee (2022) [19] point out that innovations should focus on closing the gap between disadvantaged and advantaged groups – as opposed to maintaining or even widening said gap. In other words, the ideal effect heterogeneity should benefit disadvantaged students more than advantaged ones.
There are many examples of heterogeneity in educational programs, policies, and behaviors – most of which focus on effect differentials associated with ability. In one example, researchers found that those with higher academic ability benefit more from returning to school after time in the workforce than those who return with lower abilities [7]. Others have found that learning management systems benefited students’ cognitive ability overall but negatively affected the lowest-performing students [41]. Similarly, students’ prior knowledge has also been shown to moderate the effects of feedback [14]. There is another dimension to effect heterogeneity: program features and implementations can influence the efficacy of a program. Researchers have identified effect heterogeneity based on the type and implementation of technology in schools [32, 41, 10]. Therefore, heterogeneity analyses can provide value beyond understanding who benefits the most from programs to indicate why programs are effective for which sub-groups of the population.
2.2 Effect Heterogeneity & Personalization
Personalization is a coveted goal of educational program development, especially in educational technologies [28, 13]. In theory, personalization can help create a more equitable education system [13]. For CBLPs, personalized content recommendation systems [20] and assistance delivery systems [24] have been created and tested. Mastery learning systems also provide a form of personalization as they provide students with content based on estimates of individual ability [5, 11]. Another approach to personalization is ensuring that students have access to specific programs that meet their distinct needs, similar to the approach of personalized medicine [9]. In this case, instead of expecting one CBLP to provide instruction to meet all students’ needs, each student could be prescribed a program, or even a suite of programs, that likely will maximize the benefit of their learning. Regardless of the approach, personalization is a fundamental causal question of heterogeneity: “What will benefit which students the most?" The “what" may be any educational experience: a feature, specific assistance, a piece of content, or even a whole program. Personalization is then about aligning individuals with these aspects or other aspects of their education experiences to maximize their impact on learning. There is evidence that personalization works best when aligned with student characteristics [38]. Thus, to provide students with the educational experiences that will be best for their learning, we must understand the impact of these experiences based on students’ specific characteristics.
3. CURRENT STUDY
Our current study focuses on the problem of estimating heterogeneous treatment effects not only precisely but also interpretably. Within educational research, a common approach to treatment effect heterogeneity is utilizing interaction effects in regression models [12, 41, 6]. Such models are highly interpretable as they quantify each moderator’s effect by its estimated coefficient – from which researchers can then draw statistical inferences. However, they also constrain estimated effects to be linear, which is unlikely to be the case – leading to imprecision in estimation. Alternatively, some studies have also developed advanced machine learning approaches like causal forests [2], causal boosting [23], or meta-learners [21]. While potentially more flexible and precise, the estimates from these approaches are often unparameterized and thus uninterpretable. As such, to better understand the potential complexities in effect heterogeneity necessary for personalization, there is a need to explore new methods of heterogeneous effect estimation.
For this research, we propose and discuss a new approach to estimating heterogeneous treatment effects that can balance precision and interpretability. We then apply this approach to data from a study on the effects of educational technologies with multiple treatment conditions – for which past research had found evidence for heterogeneity [12]. Besides estimating heterogeneous treatment effects, we are interested in (1) how said effects vary with a set of chosen covariates and (2) whether these differences are statistically significant under each condition as indicated by coefficients’ \(p\)-values.
4. METHOD
4.1 Study Design
The study uses open-source data from randomized control trials to explore treatment effect variability. The original sample included 3,612 students from a school district in the Southeastern United States. Many students (1,760) did not complete the posttest; we excluded them from our analyses. This attrition was attributed to a COVID spike in the U.S. at the time, which caused high absenteeism rates. However, an attrition analysis determined that the attrition was tolerable under the standards provided by the What Works Clearinghouse (WWC) of the U.S. Department of Education’s Institute of Education Sciences (IES) [12].
Based on prior state mathematics assessment scores, students were ranked within classrooms, blocked into sets of five (i.e. quintets), and then randomly assigned into either the From Here to There (40%), DragonBox (20%), Immediate Feedback (20%), or Active Control (20%) conditions. The disproportionate weighting was intended to allow researchers to focus their work on evaluating and understanding FH2T. Our analysis included 1,852 students: 755 in the From Here To There condition (FH2T), 350 in the DragonBox-12 condition (DragonBox), 381 in the Immediate Feedback condition, and 366 in the delayed feedback or Active Control condition. These conditions are described in Section 4.2. Students were expected to complete nine weekly administered, half-hour sessions in their respective programs. Teachers were asked to have students do these assignments during class hours. Students received pre- and post-test assessments (described in detail in Section 4.4) the week before and after the intervention.
4.2 Conditions
Each program taught a set of skills related to algebraic equation equivalency – including procedural ability, conceptional knowledge, and flexibility. The Immediate and Delayed conditions were administered through ASSISTments [17], an online learning platform focused primarily on math instruction. The others were stand-alone learning platforms.
4.2.1 From Here to There! (FH2T)
FH2T1 takes a gamified approach to algebra instruction by applying elements of perceptual learning [16] and embodied cognition [1]. Instead of having students solve traditional algebra equations, FH2T provides a starting expression (start state) that they must transform into a mathematically equivalent expression (goal state) using a dynamic graphical interface. Students can manipulate the expression by dragging numbers and symbols from one position to another on the screen or using a keypad when expanding terms. Only mathematically valid manipulations are accepted. Each valid manipulation counts as a step, which FH2T logs and uses to evaluate how efficiently the student transforms the expression from the start to the goal state. FH2T has 252 problems that are presented sequentially by mathematical content and complexity. Students must complete each problem to advance to the next in the sequence.
4.2.2 DragonBox-12 (DragonBox)
DragonBox2 is an educational game that provides instruction in algebraic concepts to secondary school students (ages 12-17). For each problem, students must isolate a box containing a dragon – equivalent to solving an equation for a variable \(x\). This design incorporates research-based pedagogical methods, including discovery-based learning, embedded gestures, diverse representations of concepts, immediate feedback, and adaptive difficulty [8, 39]. The game’s key innovation is that students learn algebraic rules without using or manipulating numbers or traditional algebraic symbols. Thus, students engage with the algebraic concepts as if they are puzzles. Numbers and traditional algebraic symbols are introduced gradually, presumably after the student has learned the underlying concepts. Furthermore, DragonBox applies a narrative goal to the learning: students must allow the dragon to come out of the box by isolating it in the equation. Previous analyses found that DragonBox positively affects engagement and attitudes toward math [34].
4.2.3 Immediate Feedback
The Immediate Feedback condition consisted of 218 traditional problem sets adapted from open-source curricula: namely, EngageNY, Utah Math, and Illustrative Math. The problem sequence was specifically ordered to teach the students skills built on themselves. In this condition, students could request hints while solving problems. They also received automatic feedback on whether their answer was correct or incorrect upon submission. Each problem contained a series of hints with a similar structure. The first hint gave the students the first step to answering the problem. The second hint gave the student a worked example of a similar problem. The final hint provided the student with the steps to complete the problem as well as the problem’s solution. Students could submit as many answers as needed but could not move on until they had entered the correct answer. Past research has shown this condition to be an effectual substitute for pen-and-paper homework assignments [26].
4.2.4 Active Control
The Active Control condition provided the same previous 218 problems but with post-assignment assistance – rather than on-demand hints and immediate feedback. In this condition, students could not request or receive assistance while working on or after submitting answers for each problem. They could only submit their answers once and must progress through the problem set without receiving any indication of their accuracy. At the end of each problem set, students received a report with feedback on their accuracy. They could also review their responses, revisit problems, and request hints only after completing each problem set.
4.3 Analysis Plan
Our evaluation of the effect heterogeneity requires two steps. First, we estimate the individual treatment effects (ITE) – which is the impact a treatment condition would have on students had they been assigned to it – using the Remnant-Based Leave-One-Out Potential Outcomes (ReLOOP) Estimator [15, 31]. Second, we model the ITE estimates using our heterogeneity covariates – or moderators – by employing what we are calling the Leave One Out Learner technique (LOOL). The LOOL model then estimates the conditional average treatment effects (CATE), which indicate the extent of the effects’ variation by subgroups. In the subsequent sections, we explain how ReLOOP provides unbiased ITE estimates (Section 4.3.1), how the LOOL provides interpretable CATE estimates (Section 4.3.2), and how we apply these methods to the current study’s data (Section 4.3.3).
4.3.1 ReLOOP
Consider a randomized controlled trial under the Neyman-Rubin potential outcomes framework [35, 27], in which we aim to estimate the effects of a binary treatment \(Z\) on an outcome \(Y\). In the experiment, subjects \(i = 1, 2,\dots , n\) receive random assignments to either the treatment or the control condition – denoted by \(Z_i = 1\) or \(Z_i = 0\), respectively. In addition, each subject \(i\) has associated pre-treatment covariates \(X_i\). \(Y_i(1)\) and \(Y_i(0)\) then represent subject \(i\)’s potential outcomes under the treatment and the control condition, with the observed outcome \(Y_i = Y_i(Z_i)\). We can then define the individual treatment effect (ITE) for \(i\) as \(\tau _i := Y_i(1) - Y_i(0)\). However, since we exclusively observe only \(Y_i = Y_i(1)\) for subjects assigned to the treatment group (\(Z_i = 1\)) and \(Y_i = Y_i(0)\) for those in the control group (\(Z_i = 0\)) but never both \(Y_i(1)\) and \(Y_i(0)\), \(\tau _i\) is unobservable. Nevertheless, we can estimate it using the Leave-One-Out Potential Outcomes (LOOP) Estimator [40].
We assume that the treatment assignment is a Bernoulli randomization. In other words, each subject’s treatment assignment is an independent Bernoulli trial with a constant \(\mathbb {P}(Z_i = 1) = p, 0 < p < 1\) for all \(i\) and \(Z_i \indep Z_j\) if \(i \neq j\). For each observation \(i\), we define \(m_i\) and \(U_i\) as: \begin {gather*} m_i := (1 - p) Y_i(1) + p Y_i(0) \\ U_i := \frac {Z_i - p}{p(1 - p)} = \begin {cases} 1 / p & \text {$Z_i = 1$} \\ -1 / (1 - p) & \text {$Z_i = 0$} \end {cases} \end {gather*} Wu & Gagnon-Bartsch (2018) [40] showed that if we have an estimate of \(m_i\), \(\hat {m}_i = (1 - p) \hat {Y}_i(1) + p \hat {Y}_i(0)\), such that \(\hat {m}_i \indep U_i\), then \(\hat {\tau }_i = (Y_i - \hat {m}_i)U_i\) is an unbiased estimate of \(\tau _i\). As the estimator’s name suggests, we can achieve this by leaving out observation \(i\) and imputing potential outcome estimates \(\hat {Y}_i(1)\) and \(\hat {Y}_i(0)\) with the remaining observations. For this reason, Wu & Gagnon-Bartsch (2018) [40] recommended and utilized random forests for potential outcome imputation when implementing LOOP, as out-of-bag predictions efficiently accomplish the above by default.
With LOOP, we can estimate the average treatment effect (ATE) or \(\bar {\tau } := \mathbb {E}[Y_i(1) - Y_i(0)]\) with the sample average of the estimated ITE or \(\hat {\tau }_{LOOP} = 1 / n \sum _{i}^{n}(Y_i - \hat {m}_i)U_i\). Wu & Gagnon-Bartsch (2018) [40] approximated the sampling variance of this estimate as: \[\hat {\mathbb {V}}(\hat {\tau }_{LOOP}) = \frac {1}{n} \left [\frac {1 - p}{p} \hat {M}_t^2 + \frac {p}{1 - p} \hat {M}_c^2 + 2 \sqrt {\hat {M}_t\hat {M}_c}\right ]\] where \(\hat {M}_t\) and \(\hat {M}_c\) are the mean-squared errors (MSE) of the imputed or predicted potential outcomes \(\hat {Y}_i(1)\) and \(\hat {Y}_i(0)\).
Gagnon-Bartsch et al. (2023) [15] further extended this approach by incorporating data from subjects outside the experiment who nevertheless have known covariate and outcome values (i.e. remnant data [30]) into the LOOP prediction process. Recent studies [29, 31] have shown that incorporating this data in causal estimations – specifically by fitting a model of the outcomes on covariates with the remnant data and using its predictions on the experiment data as additional covariates for the LOOP estimator – can lead to still unbiased and more precise estimates of causal effects. Sales et al. (2023) [31] dubbed this approach ReLOOP.
Overall, given a valid experiment design, LOOP and ReLOOP provide a flexible and accurate design-based covariate-adjusted method to estimate individual treatment effects: it can utilize any model so long as the leave-one-out requirement holds and does not require any additional assumptions to guarantee unbiasedness. Most importantly, this unbiasedness will hold even for inaccurate and poor-fitting models [40].
4.3.2 LOOL
For most causal inference problems, researchers are interested in estimating the ATE with the given data. However, by definition, it does not account for how each individual’s treatment effect can vary with their characteristics. Thus, for heterogeneous treatment effects, the typical measure is the conditional average treatment effect (CATE) or the average treatment effect for observations with a specific set of covariate values. We can formally define this estimand as: \[\tau (x) := \mathbb {E}[Y_i(1) - Y_i(0)|X_i = x] = \mathbb {E}[\tau _i|X_i = x]\] From this conditional expectation definition, one can see that a possible approach to estimate the CATE is regressing the ITE on the covariates – thus estimating \(\mathbb {E}[\tau _i|X_i = x]\). However, since the ITE are unobserved by design, the next best option is estimates of the ITE instead. Thus, we can fit a regression on the obtained unbiased estimates of ITE to obtain estimates of CATE. We dub this two-stage estimator the Leave-One-Out Learner or LOOL.
There are several merits to this approach. It is robust since the LOOP estimator guarantees unbiased ITE estimates. In turn, researchers can select whichever model to estimate the CATE in the second stage according to their needs – without worrying about carrying over or amplifying bias from the first. They can choose either simple parametric models for explainability in inference tasks or more complex non-parametric models for accuracy in prediction tasks. Like the meta-learner algorithms proposed by Künzel et al. (2019) [21], this allows the modeling of heterogeneous treatment effects to be incredibly flexible and adaptive. From a statistical modeling standpoint, the unbiased ITE estimates from LOOP may have higher variance than some biased ITE estimates. However, regressing them on covariates can mitigate the effect of their high variance by averaging it out. Conversely, consider alternative ITE estimates with little variance and high bias. Because of the nature of bias, averaging or regressing does not reduce the effect of their high bias. Thus, the CATE estimates provided by LOOL can be more robust than those from similar two-stage approaches.
4.3.3 Analysis Design
Our analysis employs the two methods described above. To apply ReLOOP, we first split the data into three overlapping subsets, each containing students assigned to the Active Control condition and those assigned to one of the three treatment conditions – FH2T, DragonBox, or Immediate Feedback. This splitting essentially simulates running three separate experiments, each comparing one treatment condition against the Active Control. We then use the ReLOOP procedure to estimate ITE in each subset with \(p\) equal to the sample proportion of observations under treatment. In our analysis of each subset, we treat observations under the other two treatment conditions as remnant data for each “experimental" subset. For example, for the FH2T subset, observations assigned to DragonBox and Immediate Feedback will be the remnants. Thus, we fit two models regressing the learning outcome (described in Section 4.4.2) on pre-treatment covariates (described in Section 4.4.1) with these remnants and then use their predicted values on the subset as two additional covariates. These predictions represent the outcomes the student would have gotten if their assignment was instead DragonBox and Immediate Feedback. We use a standard random forest implemented by the randomForest package in R for all of our models [22, 25]. Table 1 details the number of observations for each treatment condition and their sample proportion within each subset. With the estimated ITE from ReLOOP, we then estimate the ATE under each condition and examine their significance. In comparison, we examine the sample difference-in-means: \[\hat {\tau }_{DM} = \frac {1}{n_t} \sum _{i: Z_i = 1}^{n} Y_i - \frac {1}{n_c} \sum _{i: Z_i = 0}^{n} Y_i = \bar {Y}_{Z = 1} - \bar {Y}_{Z = 0}\] which also unbiasedly estimates the ATE with the following approximated sampling variance [18]: \[\hat {\mathbb {V}}(\hat {\tau }_{DM}) = \frac {S_t^2}{n_t} + \frac {S_c^2}{n_c}\] where \(S_t^2\) and \(S_c^2\) are the sample variance of the observed outcome \(Y_i\) in the treatment and control group, while \(n_t\) and \(n_c\) are their numbers of observations.
To examine the significance of the ATE estimates, we consider the null hypothesis of \(\bar {\tau } = 0\). Let the estimated standard error of \(\hat {\tau }\) be \(\hat {\mathbb {V}}(\hat {\tau })^{1/2}\). For a given significant level \(\alpha \), we calculate the test statistic \(T^* = |\hat {\tau } /\hat {\mathbb {V}}(\hat {\tau })^{1/2}|\) and reject the null hypothesis if \(T^* \geq \mathcal {Q}(1 - \alpha / 2)\), where \(\mathcal {Q}(1 - \alpha / 2)\) is the \(1 - \alpha / 2\) quantile of the standard normal distribution.
We then use LOOL by regressing the predicted ITE in each subset on a set of chosen covariates, which we hypothesize will be associated with effect heterogeneity, to estimate the CATE. These are the pretest algebraic knowledge, math anxiety (MA), whether the student started the year in a remote class, whether students were under an Early Intervention Program Plan (EIP), whether students had accommodations (IEP or Section 5043), and whether English is not the student’s first language (ESOL). We use a linear regression with robust or heteroskedasticity-consistent standard errors implemented by the estimatr [4] package in R: \begin {align*} &\mathbb {E}[\tau _i|X_i] = \beta _0 + \beta _1 \cdot Pretest_i + \beta _2 \cdot MA_i + \beta _3 \cdot Rmt._i \\ &+ \beta _4 \cdot EIP_i + \beta _5 \cdot Accomm._i + \beta _6 \cdot ESOL_i + \epsilon _i \end {align*}
We then perform our descriptive analysis to examine the relationship between heterogeneous treatment effects and each moderator. Further details on the variables are as below4.
| No. Observations | \(\mathbb {P}(Z_i = 1)\) | |
|---|---|---|
| FH2T | 755 | 0.674 |
| DragonBox | 350 | 0.489 |
| Immediate Feedback | 381 | 0.510 |
| Active Control | 366 | – |
| Total | 1,852 | – |
4.4 Data & Measures
This study uses open source data available through the Open Science Framework5. Our analyses utilize three different types of variables. The pre-treatment predictor variables and the learning outcomes are used in the ReLOOP models to estimate the ITE. The covariates for heterogeneity are moderators selected for the LOOL to estimate the CATE.
4.4.1 Pre-Treatment Predictor Variables
For the ReLOOP procedure, we used data from assessments administered prior to their use of their assigned condition. Pretest scores were collected by the original studies’ researchers: prior algebraic knowledge, math anxiety, and perceptual processing skills. Pretest algebraic knowledge was a variant of the learning outcome described below. The math anxiety assessment was adapted form from the Math Anxiety Scale for Young Children-Revised, which assessed negative reactions towards math, numerical inconfidence, and math-related worrying (Cronbach’s \(\alpha = 0.87\); see the items on OSF6). Five items adapted from the Academic Efficacy Subscale of the Patterns of Adaptive Learning Scale to assess math self-efficacy (Cronbach’s \(\alpha = 0.82\); see items on OSF7). The perceptual processing assessment evaluates students’ ability to detect mathematically equivalent and nonequivalent expressions as quickly as possible; see items on OSF8. The district also provided metadata on the students, including their demographics and most recent standardized state test scores in math. Demographic data included race & ethnicity, individualized education plan status (IEP), and English as a second or foreign language (ESOL) status. Missing data were imputed using single imputation with the Random Forest routine of the missForest package in R [37].
4.4.2 Learning Outcome
Students’ algebraic knowledge, which was assessed using ten multiple-choice items from a previously validated measure of algebra understanding ([36]; Cronbach’s \(\alpha = 0.89\); see the items on OSF9). Four of the items evaluated conceptual understanding of algebraic equation-solving (e.g., the meaning of an equal sign), three evaluated procedural skills of equation-solving (e.g., solving for a variable), and three evaluated flexibility of equation-solving strategies (e.g., evaluating different equation-solving strategies). Together, these ten items assessed students’ knowledge in algebraic equation-solving, the improvement of which was the goal of the interventions. Since the Active Control condition is present in all three subsets due to our design, this measure was z-scored with the mean and standard deviation of its values in the Active Control condition to improve the interpretability of parameter estimates and consistency in measurement across all subsets. As a result, the unit for treatment effects is the number of standard deviations away from the mean posttest of the Active Control group.
4.4.3 Covariates for Heterogeneity
We selected six variables as covariates for which to explore effect heterogeneity: the pretest algebraic and math anxiety scores, and whether students started the school year remotely, whether they had participated in an early intervention program prior to middle school (EIP), whether they were receiving either IEP or Section 504 accommodations in their classrooms (accommodations), and ESOL. Within each experimental subset, we standardized the chosen covariates. The continuous measures were z-scored within each experiment group. Binary measures were centered by subtracting the mean (i.e. the proportion of the sample included in that group) from each observation. In doing so, we center the model’s CATE estimates and make the estimated intercept of the LOOL regression (described in Section 4.3.3) equal to the condition’s estimated ATE with ReLOOP. The coefficients then represent effects added to or subtracted from the ATE due to unit changes in the covariates.
5. RESULTS
| ReLOOP | DM | |||||
|---|---|---|---|---|---|---|
| \(\hat {\tau }\) | SE | \(p\)-value | \(\hat {\tau }\) | SE | \(p\)-value | |
| FH2T | 0.123 | 0.048 | 0.010 | 0.108 | 0.065 | 0.096 |
| DragonBox | 0.185 | 0.056 | 0.001 | 0.189 | 0.076 | 0.013 |
| Immediate Feedback | 0.100 | 0.055 | 0.069 | 0.105 | 0.075 | 0.159 |
| Bold estimates are significant at p < 0.05 | ||||||
5.1 Individual & Average Treatment Effects
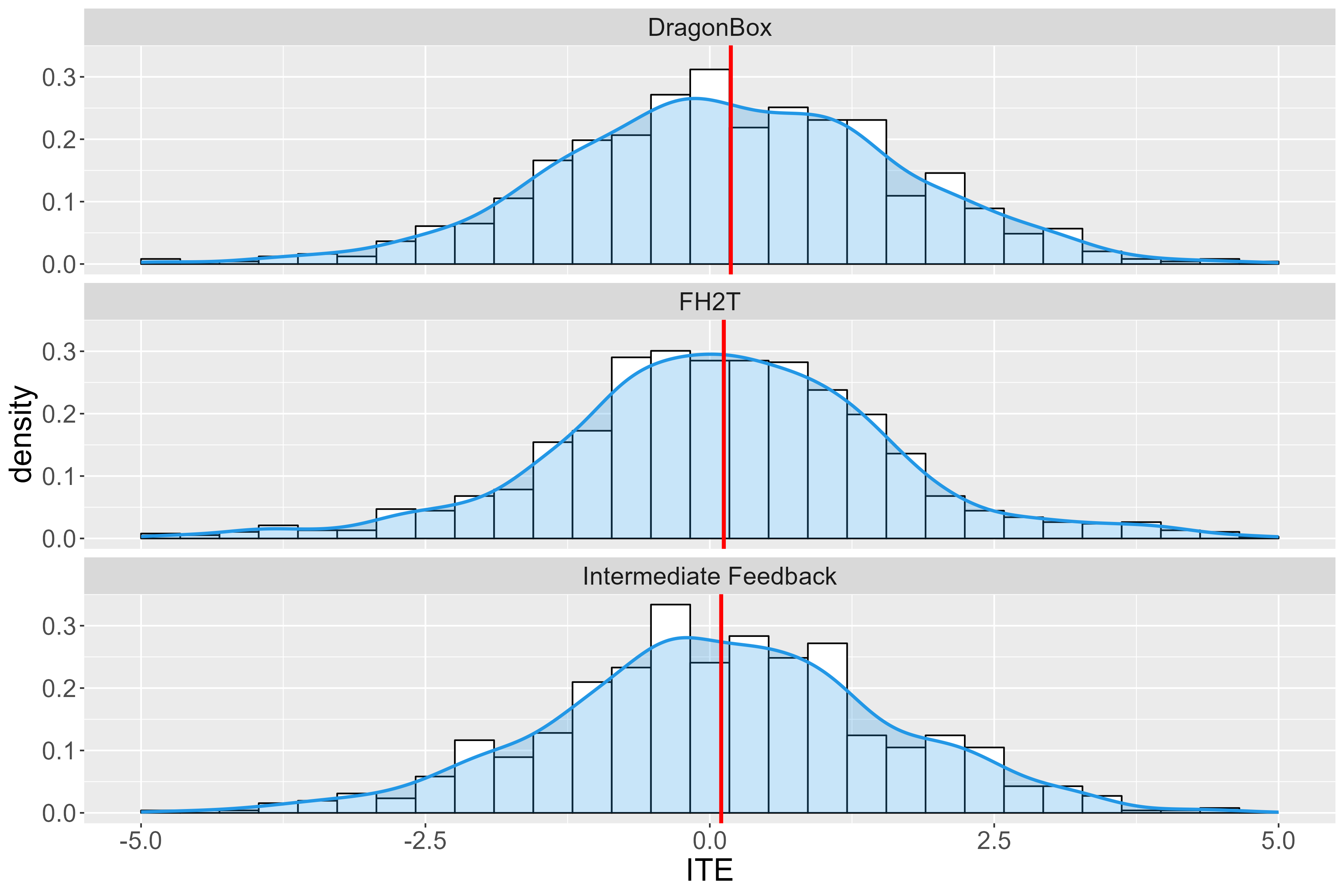
Figure 1 shows the density plot of the estimated ITE, with all three distributions being wide and highly spread out away from their means or the estimated ATE (denoted by the red lines). Under all three conditions, the standard deviation of the ITE is substantial. This result is due to the LOOP estimator trading high variance for unbiasedness, as discussed.
Table 2 shows the estimates of the ATE, the standard errors, and the \(p\)-values with each estimator. Compared to the Active Control condition, DragonBox leads to the largest increase in posttest scores – followed by FH2T and Immediate Feedback. Consider a significance level of \(\alpha = 0.05\). With ReLOOP, the estimated ATE under FH2T (\(\hat {\tau } = 0.123, \ p = 0.010\)) and DragonBox (\(\hat {\tau } = 0.185, \ p = 0.001\)) are statistically significant. With differences-in-means, however, only the estimated ATE under DragonBox is significant (\(\hat {\tau } = 0.189, \ p = 0.013\)). In addition, the ReLOOP estimator produces smaller standard errors for all three conditions, suggesting higher degrees of precision in the estimates.
5.2 Heterogeneous Treatment Effects
| FH2T | DragonBox |
Immediate Feedback | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Est. | SE | \(p\)-value | Est. | SE | \(p\)-value | Est. | SE | \(p\)-value | |
| Intercept | 0.123 | 0.047 | 0.009 | 0.185 | 0.055 | 0.001 | 0.100 | 0.054 | 0.064 |
| Pretest Math Score | 0.146 | 0.057 | 0.010 | 0.049 | 0.072 | 0.496 | 0.007 | 0.074 | 0.919 |
| Pretest Math Anxiety Score | -0.009 | 0.049 | 0.851 | -0.013 | 0.056 | 0.821 | -0.026 | 0.052 | 0.614 |
| Remote Start | -0.149 | 0.119 | 0.211 | -0.127 | 0.153 | 0.406 | 0.080 | 0.155 | 0.606 |
| EIP | 0.103 | 0.138 | 0.458 | -0.057 | 0.184 | 0.756 | 0.042 | 0.150 | 0.780 |
| Accommodations | 0.015 | 0.166 | 0.930 | -0.050 | 0.189 | 0.794 | 0.116 | 0.153 | 0.447 |
| ESOL | -0.309 | 0.131 | 0.018 | -0.345 | 0.155 | 0.026 | -0.339 | 0.176 | 0.055 |
Bold estimates are significant at p < 0.05 | |||||||||
Table 3 shows the values and standard errors of coefficients along with the \(p\)-values in the regression model estimating the CATE under each condition. Under all three conditions, most chosen covariates’ effects on a student’s CATE are not statistically significant. The only exception is the pretest score under FH2T (\(\hat {\beta } = 0.146, \ p = 0.010\)) and ESOL under both FH2T (\(\hat {\beta } = -0.309, \ p = 0.018\)) and DragonBox (\(\hat {\beta } = -0.345, \ p = 0.026\)). The magnitudes of the coefficients for ESOL are roughly twice those of the intercepts or the estimated ATE for FH2T (\(\hat {\tau } = 0.123, \ \hat {\beta } = -0.309\)) and DragonBox (\(\hat {\tau } = 0.185, \ \hat {\beta } = -0.345\)). Thus, being ESOL strongly and adversely impacts a student’s estimated CATE in both conditions. This result suggests that these conditions penalize ESOL students more on average than the Active Control condition. Similarly, under FH2T, relative to the estimated ATE (\(\hat {\tau } = 0.123\)), the pretest math score leads to a sizable increase in the estimated CATE (\(\hat {\beta } = 0.146\)). This result suggests that students with better algebra foundations benefit more from FH2T, compared with the Active Control condition, than students with weaker algebra foundations on average.
In addition, we fitted a regression with interaction effects to estimate the posttest with each subset – shown in Table 4 – whose coefficients of the treatment and its interactions are analogs to the intercept and coefficients in Table 3. The standard errors of all coefficients in Table 3 are smaller than those of the coefficients of the interaction effects in Table 4 except for Accommodation under FH2T \((0.166 > 0.163)\). Like ReLOOP in Table 2 above, this result suggests the LOOL provides more precise estimates of the coefficients.
| FH2T | DragonBox |
Immediate Feedback | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Est. | SE | \(p\)-value | Est. | SE | \(p\)-value | Est. | SE | \(p\)-value | |
| Intercept | 0.014 | 0.041 | 0.740 | 0.022 | 0.041 | 0.596 | 0.016 | 0.041 | 0.693 |
| Pretest Algebra Score | 0.452 | 0.054 | 0.000 | 0.444 | 0.053 | 0.000 | 0.452 | 0.054 | 0.000 |
| Pretest Math Anxiety | -0.070 | 0.041 | 0.089 | -0.069 | 0.041 | 0.089 | -0.070 | 0.041 | 0.089 |
| Remote Start | 0.469 | 0.115 | 0.000 | 0.469 | 0.115 | 0.000 | 0.469 | 0.115 | 0.000 |
| EIP | -0.325 | 0.106 | 0.002 | -0.325 | 0.106 | 0.002 | -0.325 | 0.106 | 0.002 |
| Accommodations | -0.094 | 0.129 | 0.463 | -0.094 | 0.129 | 0.464 | -0.094 | 0.129 | 0.464 |
| ESOL | 0.118 | 0.112 | 0.295 | 0.118 | 0.112 | 0.295 | 0.118 | 0.112 | 0.295 |
| Z (Treatment) | 0.086 | 0.050 | 0.085 | 0.141 | 0.059 | 0.017 | 0.066 | 0.058 | 0.253 |
| Pretest Algebra Score \(\cdot \) Z | 0.162 | 0.064 | 0.011 | 0.112 | 0.076 | 0.141 | 0.025 | 0.078 | 0.750 |
| Pretest Math Anxiety \(\cdot \) Z | 0.016 | 0.050 | 0.744 | 0.016 | 0.060 | 0.795 | -0.037 | 0.056 | 0.514 |
| Remote Start \(\cdot \) Z | -0.190 | 0.136 | 0.165 | -0.139 | 0.165 | 0.399 | 0.028 | 0.169 | 0.870 |
| EIP \(\cdot \) Z | 0.169 | 0.140 | 0.229 | 0.176 | 0.197 | 0.372 | 0.209 | 0.150 | 0.164 |
| Accommodations \(\cdot \) Z | 0.019 | 0.163 | 0.909 | 0.027 | 0.189 | 0.887 | 0.068 | 0.165 | 0.680 |
| ESOL \(\cdot \) Z | -0.292 | 0.138 | 0.035 | -0.456 | 0.172 | 0.008 | -0.339 | 0.180 | 0.060 |
Bold estimates are significant at \( p < 0.05\). |
|||||||||
Note: Only the significance of coefficients of the treatment and its interaction effects is reported. | |||||||||
6. DISCUSSION
The analysis reveals two notable trends. First, one of the conditions (FH2T) is likely only effective for students who start the program with average or above-average prior knowledge. This is consistent with what previous analyses of this experiment found [12], which provides some validation of the LOOL method. Those who are below average would likely have benefited from being in the Active Control condition. This may be due to the nature of the program, which expected students to learn concepts and procedures in algebra without direct instruction. Lower-knowledge students may not have had a basis in algebra to intuit these knowledge components, thus driving the heterogeneity. The second trend is slightly less intuitive; two of the conditions (FH2T and Dragon Box) produced reduced potentially negative effects for students who were English Speakers of Other Languages (ESOL). This was found even after accounting for the influence of any potential differences in prior knowledge. Notably, both these conditions contained limited written or spoken English, focusing on mathematical notation or visual repressions of math (e.g., objects instead of numbers or variables). Alternatively, the Active Control condition includes instructions and word problems written in English. Thus, it would seem plausible that FH2T and Dragon Box would be more accessible to students who may not yet be proficient in English than the Active Control condition. Yet our findings indicate otherwise. More work is needed to explore the driving these trends, but for now, it highlights the need to explore effect heterogeneity, which may follow unexpected patterns. Overall, both of these findings fit into the framework established by Kizilcec & Lee (2022), that innovations can be categorized as maintaining, widening, or closing gaps between advantaged and disadvantaged groups [19]. In the present case, we have found that the two most innovative programs – FH2T and Dragon Box – fall into the category of widening the learning gap for two important populations: students with lower prior knowledge and English Speakers of Other Languages. Further emphasizing the need to ensure that programs are optimized to work well for all students, but especially those who need good instruction the most.
In terms of the estimation of the ATE, ReLOOP improved the precision of the estimates, as seen by the lower standard errors for all three conditions compared to the difference-in-means. This is consistent with findings from past studies [15, 31]. Likewise, the LOOL provided more precise estimates than a similar interaction model using the same moderators.
7. CONCLUSION
The findings of this study demonstrate the utility of the ReLOOP and LOOL methods for understanding heterogeneous effects and suggest that these methods can be used to pursue the personalization of educational programs. In essence, personalization is a question of individual treatment effects, as this ideal is based on the assumption that each student will experience different benefits from specific educational experiences. The goal, therefore, is to construct learner experiences that optimize each student’s learning individually, not just leaner benefits on average. This requires us to understand more about whether an effect is dependent on student characteristics and how we can tailor educational experiences to maximize effectiveness.
8. ACKNOWLEDGEMENT
The research reported here was supported by the Institute of Education Sciences, U.S. Department of Education, through Grant R305D210031. The opinions expressed are those of the authors and do not represent views of the Institute or the U.S. Department of Education.
9. REFERENCES
- D. Abrahamson, M. J. Nathan, C. Williams-Pierce, C. Walkington, E. R. Ottmar, H. Soto, and M. W. Alibali. The future of embodied design for mathematics teaching and learning. Frontiers in Education, 5, 2020.
- S. Athey and S. Wager. Estimating treatment effects with causal forests: An application. Observational studies, 5(2):37–51, 2019.
- M. L. Bernacki, M. J. Greene, and N. G. Lobczowski. A systematic review of research on personalized learning: Personalized by whom, to what, how, and for what purpose (s)? Educational Psychology Review, 33(4):1675–1715, 2021.
- G. Blair. estimatr: Fast estimators for design-based inference. R package version 030., 2021.
- B. S. Bloom. Learning for mastery. instruction and curriculum. regional education laboratory for the carolinas and virginia, topical papers and reprints, number 1. Evaluation Comment, 1(2), May 1968. issue: 2 container-title: Evaluation Comment volume: 1 ERIC Number: ED053419.
- P. Boedeker and R. K. Henson. Evaluation of heterogeneity and heterogeneity interval estimators in random-effects meta-analysis of the standardized mean difference in education and psychology. Psychological Methods, 25(3):346, 2020.
- D. Card. The causal effect of education on earnings. Handbook of labor economics, 3:1801–1863, 1999.
- G. A. Cayton-Hodges, G. Feng, and X. Pan. Tablet-based math assessment: What can we learn from math apps? Journal of Educational Technology Society, 18(2):3–20, 2015.
- I. S. Chan and G. S. Ginsburg. Personalized medicine: progress and promise. Annual review of genomics and human genetics, 12:217–244, 2011.
- A. C. Cheung and R. E. Slavin. How features of educational technology applications affect student reading outcomes: A meta-analysis. Educational Research Review, 7(3):198–215, 2012.
- A. T. Corbett and J. R. Anderson. Knowledge tracing: Modeling the acquisition of procedural knowledge. User Modeling and User-Adapted Interaction, 4(4):253–278, Dec. 1994.
- L. E. Decker-Woodrow, C. A. Mason, J.-E. Lee, J. Y.-C. Chan, A. Sales, A. Liu, and S. Tu. The impacts of three educational technologies on algebraic understanding in the context of covid-19. AERA open, 9:23328584231165919, 2023.
- H. Dumont and D. D. Ready. On the promise of personalized learning for educational equity. Npj science of learning, 8(1):26, 2023.
- E. R. Fyfe and B. Rittle-Johnson. Feedback both helps and hinders learning: The causal role of prior knowledge. Journal of Educational Psychology, 108(1):82, 2016.
- J. A. Gagnon-Bartsch, A. C. Sales, E. Wu, A. F. Botelho, J. A. Erickson, L. W. Miratrix, and N. T. Heffernan. Precise unbiased estimation in randomized experiments using auxiliary observational data. Journal of Causal Inference, 11(1):20220011, 2023.
- R. L. Goldstone, D. H. Landy, and J. Y. Son. The education of perception. Topics in Cognitive Science, 2(2):265–284, 2010.
- N. T. Heffernan and C. L. Heffernan. The assistments ecosystem: Building a platform that brings scientists and teachers together for minimally invasive research on human learning and teaching. International Journal of Artificial Intelligence in Education, 24(4):470–497, Oct. 2014.
- G. W. Imbens and D. B. Rubin. Causal inference in statistics, social, and biomedical sciences. Cambridge University Press, 2015.
- R. F. Kizilcec and H. Lee. Algorithmic fairness in education. Taylor Francis, 2022. arXiv:2007.05443 [cs].
- S. S. Kundu, D. Sarkar, P. Jana, and D. K. Kole. Personalization in education using recommendation system: an overview. Computational Intelligence in Digital Pedagogy, pages 85–111, 2021.
- S. R. Künzel, J. S. Sekhon, P. J. Bickel, and B. Yu. Metalearners for estimating heterogeneous treatment effects using machine learning. Proceedings of the national academy of sciences, 116(10):4156–4165, 2019.
- A. Liaw, M. Wiener, et al. Classification and regression by randomforest. R news, 2(3):18–22, 2002.
- S. Powers, J. Qian, K. Jung, A. Schuler, N. H. Shah, T. Hastie, and R. Tibshirani. Some methods for heterogeneous treatment effect estimation in high dimensions. Statistics in medicine, 37(11):1767–1787, 2018.
- E. Prihar, A. Sales, and N. Heffernan. A bandit you can trust. In Proceedings of the 31st ACM Conference on User Modeling, Adaptation and Personalization, pages 106–115, 2023.
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria, 2022.
- J. Roschelle, M. Feng, R. F. Murphy, and C. A. Mason. Online mathematics homework increases student achievement. AERA open, 2(4):2332858416673968, 2016.
- D. B. Rubin. Bayesian inference for causal effects: The role of randomization. The Annals of statistics, pages 34–58, 1978.
- V. V. Sadovaya, O. V. Korshunova, and Z. Z. Nauruzbay. Personalized education strategies. International Electronic Journal of Mathematics Education, 11(1):199–209, 2016.
- A. C. Sales, A. Botelho, T. M. Patikorn, and N. T. Heffernan. Using big data to sharpen design-based inference in a/b tests. In Proceedings of the 11th International Conference on Educational Data Mining. International Educational Data Mining Society, pages 479–486, 2018.
- A. C. Sales, B. B. Hansen, and B. Rowan. Rebar: Reinforcing a matching estimator with predictions from high-dimensional covariates. Journal of Educational and Behavioral Statistics, 43(1):3–31, 2018.
- A. C. Sales, E. B. Prihar, J. A. Gagnon-Bartsch, N. T. Heffernan, et al. Using auxiliary data to boost precision in the analysis of a/b tests on an online educational platform: New data and new results. Journal of Educational Data Mining, 15(2):53–85, 2023.
- R. F. Schmid, R. M. Bernard, E. Borokhovski, R. M. Tamim, P. C. Abrami, M. A. Surkes, C. A. Wade, and J. Woods. The effects of technology use in postsecondary education: A meta-analysis of classroom applications. Computers & Education, 72:271–291, 2014.
- L. Schudde. Heterogeneous effects in education: The promise and challenge of incorporating intersectionality into quantitative methodological approaches. Review of Research in Education, 42(1):72–92, 2018.
- N. M. Siew, J. Geofrey, and B. N. Lee. Students’ algebraic thinking and attitudes towards algebra: The effects of game-based learning using dragonbox 12 + app. The Research Journal of Mathematics and Technology, 5(1), 2016.
- J. Splawa-Neyman, D. M. Dabrowska, and T. P. Speed. On the application of probability theory to agricultural experiments. essay on principles. section 9. Statistical Science, pages 465–472, 1990.
- J. R. Star, C. Pollack, K. Durkin, B. Rittle-Johnson, K. Lynch, K. Newton, and C. Gogolen. Learning from comparison in algebra. Contemporary Educational Psychology, 40:41–54, 2015.
- D. J. Stekhoven and P. Bühlmann. Missforest—non-parametric missing value imputation for mixed-type data. Bioinformatics, 28(1):112–118, 2012.
- L. Tetzlaff, F. Schmiedek, and G. Brod. Developing personalized education: A dynamic framework. Educational Psychology Review, 33:863–882, 2021.
- R. Torres, Z. O. Toups, K. Wiburg, B. Chamberlin, C. Gomez, and M. A. Ozer. Initial design implications for early algebra games. In Proceedings of the 2016 Annual Symposium on Computer-Human Interaction in Play Companion Extended Abstracts, CHI PLAY Companion ’16, page 325–333, New York, NY, USA, Oct. 2016. Association for Computing Machinery.
- E. Wu and J. A. Gagnon-Bartsch. The loop estimator: Adjusting for covariates in randomized experiments. Evaluation review, 42(4):458–488, 2018.
- D. Yan and G. Li. A heterogeneity study on the effect of digital education technology on the sustainability of cognitive ability for middle school students. Sustainability, 15(3):2784, 2023.
1https://graspablemath.com/projects/fh2t
2https://dragonbox.com/products/algebra-12
3EIP and Section 504 are both accommodation plans for students with disabilities – mandated by U.S. Federal Law.
4Replication code available at https://osf.io/f7rb4/
5https://osf.io/r3nf2/ The data can be accessed after
submitting a data sharing agreement.