ABSTRACT
Research on the effectiveness of Intelligent Tutoring Systems (ITSs) suggests that automatic hint generation has the best effect on learning outcomes when hints are provided on the level of intermediate steps. However, ITSs for programming tasks face the challenge to decide on the granularity of steps for feedback, since it is not a priori clear which sequence of code edits constitutes a step. We argue that the step granularity for programming tasks should be founded on pedagogical considerations and suggest Vygotsky’s theory as an example. Furthermore, we compare several automated methods for sub-dividing programming traces into steps. To evaluate these methods, we provide a novel dataset consisting of 44 code-traces from introductory Python tasks. Furthermore, we provide a novel tool for annotating steps in programming traces and perform a study with six experienced annotators. Our post-survey results show that the annotators favored solved subtasks as a granularity for step division. However, our results show that completed lines as indications of steps explain the annotations best, suggesting that even simple rule-based approaches are suitable for automatic programming trace sub-division.
Keywords
1. INTRODUCTION
Intelligent Tutoring Systems (ITS) have been shown to be most effective if they provide learners with pedagogically valuable hints at intermediate steps while solving a task [11, 24]. One particularly popular hinting strategy in the context of programming are next-step hints [13] which try to predict what a learner should do next to get closer to a correct solution on a path that matches their intent and abilities. However, to provide a helpful next-step hint, one must define what a step is (for this learner). Giving only one symbol as a next-step hint is probably too fine-grained, while disclosing the entire correct solution is probably too coarse – and could potentially hinder learning [7]. So, what is a reasonable granularity for giving a next-step hint in programming tasks, and how can the solution process of a programming task be effectively sub-divided into steps? Prior work has emphasized the importance of these questions [8], and some authors explicitly define what they consider to be a step in their work [2, 20, 14]. Often, the step granularity is determined implicitly by a combination of the logging granularity of the system at hand and the method used for hint generation [13, 18]. However, the diversity of step definitions raises the question: which step definition is most suitable for a given context, and are there insights from educational and cognitive science perspectives that may help us choose? This paper provides, to our knowledge, the first systematic comparison of step definitions for programming tasks and their operationalization.
We have collected and implemented a range of approaches from the literature that can automatically subdivide programming traces into steps. These approaches were adjusted for text-based Python programming. We then performed a study with six students with programming and/or tutoring experience (annotators), who were asked to extract steps from a range of anonymized programming traces from CS undergrad students (learners) solving introductory Python tasks. We evaluate the automated approaches using the annotated programming traces, and find that, in our set of tasks, most steps were identified at the level of completed lines of code. The main contributions of this paper are:
- A novel tool for annotating steps in programming traces from students.
- An annotated dataset of 44 programming traces for 18 tasks with at least two traces per task and three or more annotations per trace.
- A systematic evaluation of several step detection methods from the literature, covering both the theoretical foundations and their empirical performance when compared to human annotations.
The source code of the annotation tool (Section 4.1), as well as the analysis code and dataset1, are open source.
2. BACKGROUND AND RELATED WORK
Presently, there is no universally accepted definition of steps in a programming task. The step definition might be influenced by factors like the theoretical perspective, the task domain, and the skill level of a learner. For instance, Jeuring et al. differentiate between "steps" and "subgoals" in programming tasks [9]. A step is viewed as either a code-edit or a user-action within the code environment. A subgoal is seen as the intention behind a sequence of steps that lead to progress towards the solution. Therefore, the implementation of a subgoal could be described with an intention (a plan) and a set of steps that implement it. We find this distinction very insightful for analysing parallel levels of granularity. However, we argue that the issue of determining a granularity for a subgoal raises questions similar to those surrounding the granularity of individual steps. In particular, we cannot decide if the intention of a learner in doing a certain step is to complete a small feature or a subgoal on a higher level. Furthermore, it is very likely that multiple levels of intentions exist simultaneously. Therefore, in this work, we simplify our terminology and consider only steps as the relevant entity for providing hints. More precisely, we define a step as any sequence of code-edits and/or user-actions that follows a distinct intention on a granularity determined by pedagogical considerations. In the following, we discuss potential theoretical foundations for step definitions.
2.1 Pedagogical foundation
One foundation for next-step hints is Vygotsky’s learning theory [25]. For providing automated hints, considering the Zone of Proximal Development (ZPD) is especially useful. The ZPD characterises the area of competency that is acquirable by the learner if assistance is provided. Vygotsky’s learning theory states that the progression in competency is fastest if learning opportunities lie in this zone. Scaffolding operationalizes the ZPD for giving feedback through hints [7]. It states that hints should contain as little information as necessary to enable the learner to progress on a task themselves. Based on scaffolding theory, we argue that the pedagogically optimal granularity on which to provide a next-step hint might be related to the students competency and ZPD. More precisely, we aim for the granularity of a slightly higher competency compared to the learner but which is still accessible and actionable for the learner.
2.2 Cognitive science perspective
Cognitive science concepts can also contribute to reasoning about steps. Different foundations in cognitive science motivate different operationalizations, which in turn can be translated into automatic algorithms to sub-divide programming traces into steps.
Cognitive load theory aligns with Vygotsky’s learning theory [23]. It provides a perspective on the question how and why learners might sub-divide their task-solution process. If a learner solves a task, they have to allocate chunks of information to their limited working memory. Cognitive load refers to the amount of memory occupied, which is usually related to the proficiency in a certain domain. Proficiency allows working memory items to be used more effectively. Consequently, if the cognitive load is too high, learning can be hindered [15]. This implies that the sub-division of a task should be on a granularity that is not too coarse in order to keep cognitive load in check. Additionally, there is a relation between pausing behavior in keystroke patterns and cognitive load [23], providing a measurable indicator of potential cognitive processes.
Learners with a higher proficiency tend to experience less cognitive load when solving tasks. This phenomenon can be connected to cognitive schemas. A schema is a cognitive construction that reflects and structures information in an actionable way [15]. They can be utilized to increase the effectiveness of working memory use. It is plausible that steps of learners who have built more effective schemas might be more coarse-grained [6]. We additionally hypothesize that a learner’s individual schema could be a reasonable granularity for providing hints. Duran et al.’s work builds a bridge between cognitive schemas and the complexity of real-word programming tasks [5]. The authors propose a hierarchical model for analysing the cognitive complexity of programs using a plan tree. A plan tree is a representation of a program in plans of different levels, where a higher level plan consists of multiple lower level plans. The complexity of programs can be compared with the plan depth (tree height) of the plan tree. It is hypothesized to be associated with cognitive load and mediated by the amount and complexity of schemas accessible to the learner. In an optimal case, plan trees could provide a tool to select a step granularity based on the plan tree level.
2.3 Implementations of Step concepts
When giving a next-step hint, a step sub-division method is always present either implicitly or explicitly. We categorize existing methods for step sub-division in three broad overlapping categories: structural, dynamic, and behavior-based. Various combinations and hybrid approaches of these categories also exist.
Structural approaches focus on the static properties of code snapshots and their relations. In particular, this includes approaches that utilize the raw string of the snapshot and approaches based on static code analysis, for instance via abstract syntax trees (ASTs). One example is to assign steps on the level of completed lines. Roest et al. used three rules for this[20]: Firstly, snapshots with an incorrect syntax are removed from the trace. Next, duplicate states are identified and deleted. Lastly, only the last edit of each line is kept. Another structural approach is implemented by Birillo et al. [2]. They used static code analysis to provide three heuristics on the level of six different control-flows. The first heuristic is based on summarizing changes that contribute to adding a new control block. The second heuristic covers changes that modify the control flow of a single, already existing control structure. Lastly, one heuristic covers changes to the body (content) of a particular control structure. Many structural approaches utilize learner data to infer a state space for each task [19, 26]. The state space size is usually reduced by preprocessing the code and mapping the ASTs for different solutions onto one state [19]. Depending on how much the state space is reduced, one obtains different granularities. For instance Zhi et al. use \(pq\)-grams to reduce the state space considerably [26].
Dynamic approaches are relying on the execution behavior of snapshots. One basic approach is to consider the set of passed unit-test cases as a state and assign a step once at least one unit test changes from fail to pass or vice versa [14]. Alternatively, the execution behavior can be analyzed in more detail by computing distances between execution traces [17].
Behavior-based approaches assign steps to actions that the learner performs or log-events that get triggered. One such approach would be to examine the pausing behavior of learners [23]. One can also use submissions and feedback requests as an indicator of steps [9].
3. METHOD
In this section we will review several methods from the literature that could be used to sub-divide programming traces into steps. We describe how we implemented these Methods for Python programming traces in our dataset. Additionally, we will exemplify the methods with a case-study.
3.1 Trace sub-division methods
Our goal is to implement different methods that cover the range of approaches present in the literature. We note that, due to practical limitations, we could not ensure that every method is selected and optimized in a way that would allow a conclusive judgement. We applied and evaluated all methods on cleaned code traces where we deleted all snapshots between the first and last occurrence of any exact duplicate present.
Our first approach is the completed line approach from Roest et al. as described above [20]. We also adapted Birillo et al.’s approach for trace sub-division on control-flow level [2] with the heuristics "Add control block", "Modify control flow", and "Internal body change" on various Python control structures (For, While, If, With, FunctionDef, Return, Try, ExceptionHandler). Since it was already used in downstream work to determine sub-goals in programming tasks [12], we decided to represent state-space based methods using parts of Zhi et al.’s state-space reduction method [26]. More precisely, we extract \(pq\)-grams from all correct solutions for \(p \in \{1,2,3\}\) and \(q \in \{1,2,3,4\}\) (similar to [26]) and match all \(pq\)-grams that have a Jaccard-similarity (on all snapshots) over 0.975. We do not apply further processing of the resulting sets of shapes into disjunction shapes and features (like [26] do), since the number of states was reduced to very small numbers in our dataset when applying processing beyond the matching of code shapes.
We also created two sub-division methods based of behavioral patterns of the learners. Firstly, we classified every code-action within the UI as a step. This includes running the program, requesting feedback, and submitting code for testing. A second behavior-based approach focuses on the relationship between cognitive load and pausing behavior [23]. We hypothesize that pausing behavior can therefore indicate if a learner is stuck at a certain point in the solution process, which would be relevant information with respect to automatic hint generation. Pausing behavior might also indicate that a step has been completed. Therefore, we mark all instances of a pause in typing for more than 2 seconds as a step. We choose the cutoff of two seconds based on a previously published dataset [16].
Furthermore we propose three different autoregressive, distance-based methods for trace sub-division. Each of these methods defines a distance measure between two snapshots. A new step is marked as soon as the distance to the last step exceeds a certain threshold. We included these approaches in order to be able to account for any distance-based method. However, the auto-regressive nature of this approach might be prone to accumulating errors for longer sequences of snapshots. First, we consider the distance between code execution traces proposed by [17]. We use easy positive examples for each task for the generation of execution traces with a threshold of 0.01. Second, we consider the distance between code embeddings produced using the PromptEOL method and CodeLlama 7B with a threshold of 0.02 [10, 21, 3]. Lastly we use the Levenshtein distance on the code snapshots as a baseline (threshold=8). The thresholds were optimized based on the performance on a small, independent sample dataset of annotations created by the authors.
3.2 Case study
* Number out of two annotators who selected a snapshot as step.
Table 1 shows an example code trace of a learner. The columns indicate whether a certain step subdivision method would treat the current snapshot as a step or not (autoregressive methods were excluded for better oversight). In the rightmost column, we have displayed the step selection of the annotators of our annotation study (section 4). The task for the learner was to implement a function that calculates the factorial of an integer \(n\). In the first section of the trace, the learner fixes an issue with the first return statement. The annotators regard the third snapshot to be a completed step. All other methods agree with the exception that there was no code-action performed by the learner. Further down, the annotators selected two more snapshots as steps, with only the line-based method agreeing on all three occasions. All methods seem to display some false positives. One interesting case is the third and second snapshot from the bottom, where it becomes apparent that formatting code (in this case removing a space) can trigger completed line and control structure steps. This occurs when the formatting occurs in distinct lines or blocks. We decided to display formatting to our annotators in order enable them to understand student activity on a keystroke level. However, this decision might have a slight negative influence on the performance of certain methods.
4. STUDY
In order to evaluate the different trace sub-division methods, we performed a study with six annotators. As data source for programming traces, we recorded the coding behavior of 62 learners in a two-hour Python introduction course with third-semester undergrad students held in October 2024. For this course, we utilized SCRIPT, which is our own programming ITS [4]. LLM-generated textual hints could be requested through the system’s UI. We obtained 399 traces on 18 different tasks. In this section, we will discuss the setup for the study as well as the tool we have developed for the annotation procedure. Both studies—the Python introduction course for trace collection, and the annotation study—were approved by the local ethics comity.
4.1 Annotation tool
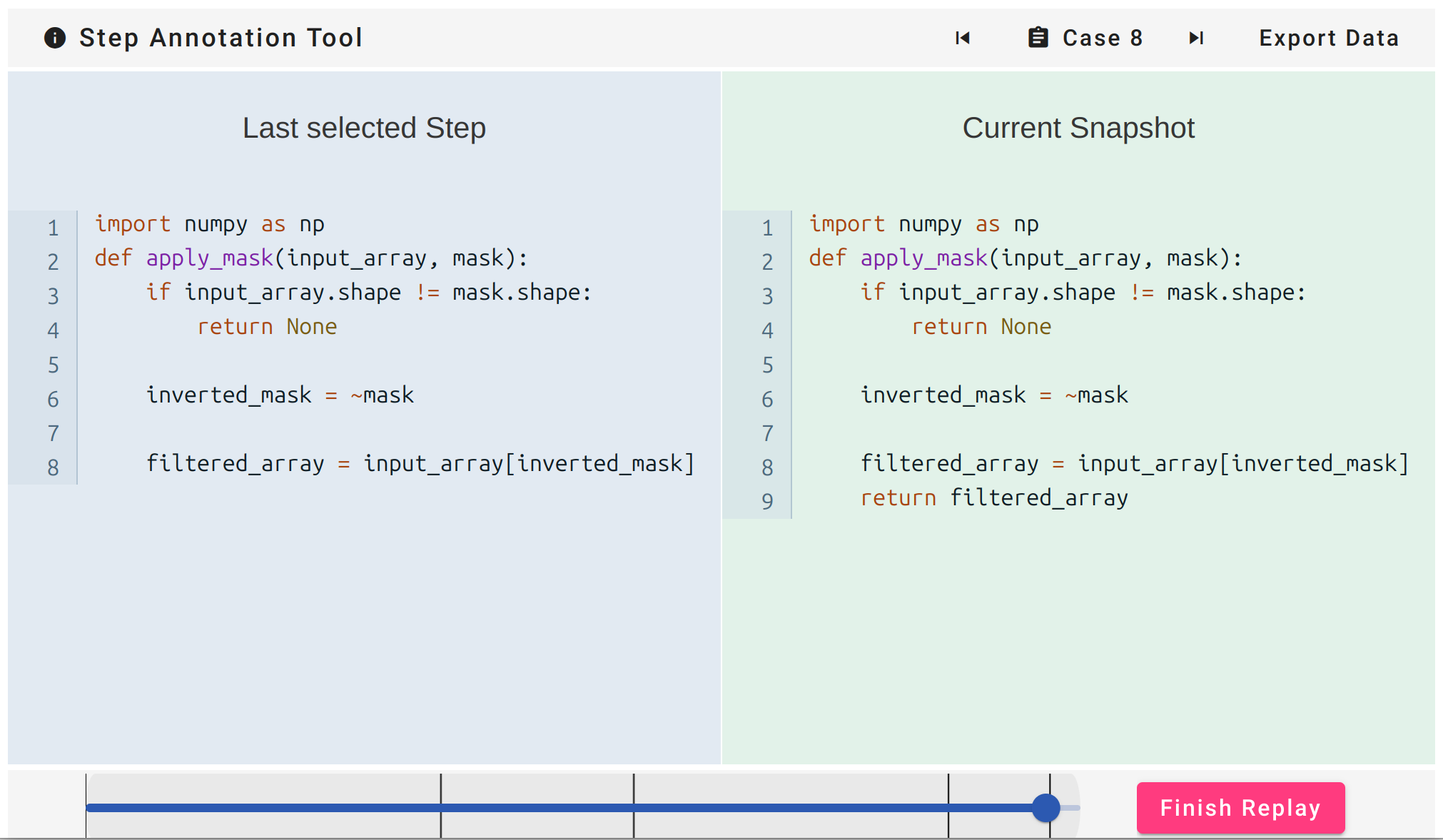
As displayed in Figure 1, our novel step annotation tool consists of three main components. The toolbar at the top contains a button to display relevant information (annotation guidelines, task descriptions), arrow icons to navigate across different code traces (cases), and a button to export the annotated dataset. The center panels contain code snapshots. On the left side, the annotator can review the last snapshot that was labelled as a step. On the right side, the current snapshot is displayed. It can be marked and unmarked with a mouse-click, leading to a change in background color from blue to green and vice-versa. We intentionally did not include a commentary function in order to streamline the annotation process and limit the (time-)cost of annotation for annotators. The bottom toolbar features a slider for the current code trace, where black bars indicate annotated steps. The slider value represents an index in the sequence of snapshots at keystroke level, but is not associated with actual passed time. The Finish Replay button navigates to the next trace. The tool is implemented as a frontend-only web-application with Angular 19. The data management of the tool allows uploading code traces directly via the UI and backs up annotations in local storage for later restoration in case of browser crashes. The source code with build instructions is available as a GitLab repository2. We included the system usability questionnaire [1] into the post survey of our annotation study to ensure that the usability of the annotation tool is sufficient to not negatively impact data quality. We obtained an average usability score of 87.08, corresponding to an A+ usability grade [22].
4.2 Study setup
In order to create datasets for the annotation study, we obtained a difficulty parameter for each task using a two-parameter Item Response Theory (IRT) model. For the purpose of IRT, we counted an attempt as successful if the learner was able to solve the task within the median solution time across all tasks. We then sampled three learner traces per task randomly and reviewed each of the traces to ensure their suitability for annotation. We found several traces that could not be used due to copy and pasting of larger chunks and detours from the task goal. For two tasks, we had to re-sample and review additional traces (three in total) in order to meet our goal of two suitable traces per task. In total, we obtained 44 traces, which we grouped into three datasets, two primary sets and one bonus set (see Figure 2). For the two primary sets, we selected a set of four traces of very easy tasks as a common starting point. We displayed the remaining tasks in increasing order of difficulty, the first set contained the eight easiest tasks and the second set contained the six most difficult tasks. We assigned sets to the participants based on their prior Python experience, giving harder tasks to more experienced annotators (48 months median Python experience) and easier tasks to less experienced annotators (16 months median Python experience). We gave participants who finished early an additional set of bonus traces, where we didn’t differentiate by difficulty. Each study session was set for 90 minutes with 10 min at the beginning allocated for system explanation and initial questions and 15 min at the end allocated for the post-questionnaire and debriefing. We excluded two of the 44 traces from further analysis due to collecting less than three annotations for them.
We provided the participants with an information sheet containing a general study description and a consent form at the beginning of the study. Additionally, we provided annotation guidelines that were shown at the beginning of annotation and accessible during the whole process by clicking on the info icon of the Annotation tool. Importantly, we wished to avoid biasing annotators into the direction of any specific step definition described in Section 2. Therefore, we provided only loose guidelines, as well as guidelines for some Python-specific more technical cases. The main prompt we gave our annotators was to "immerse [themselves] into the solution-process of a particular student" and to mark steps where they believe "that the student completed a small chunk of their process towards the correct solution". The full agreement form as well as the annotation guidelines are provided in the GitLab repository. We recruited our participants using public E-Mail lists at Bielefeld university and E-Mail lists of university courses. Two participants were also recruited in-person. As we wanted to get a picture about step definitions of persons with programming experience slightly above undergrad level but not yet full professionals, the main inclusion criterion for the study was studying an IT-related subject and having extensive Python experience. Applying this procedure, we recruited six annotators and collected 194 annotated traces in total.
4.3 Metrics
Our metric of success for automatic step sub-division algorithms is how well the respective algorithm matches human step annotations. We quantify the match in terms of classification metrics, namely F1 score, accuracy, true positive rate, and true negative rate. More precisely, let \(x_{i,j,s} \in \{0,1\}\) denote whether annotator \(i \in \{1,2,...,N\}\) annotated snapshot \(s \in \{1,2,...,S_j\}\) of trace \(j \in \{1,2,....,J\}\) as a step (1 means yes, 0 means no). Correspondingly, let \(y_{m,j,s} \in \{0,1\}\) denote whether method \(m \in \{1,2,...,M\}\) classified snapshot \(s\) in trace \(j\) as a step. Then, we define the true negatives \(\text {TN}_{i,m}\) for annotator \(i\) and method \(m\) as the number of snapshots where both \(x_{i,j,s}\) and \(y_{m,j,s}\) are zero.
For the true positives, we choose to include a slack parameter, since steps are typically sparse in our fine-granular data and it may be slightly ambiguous at which keystroke exactly to set the step (e.g., should the ":" at the end of a control structure be included or not?). So, given a slack of \(\delta \in \mathbb {N}^0\) snapshots, we define the set \(\Delta _{m,j,s}(\delta ) := \{ y_{m,j,s-\delta },\ldots ,\) \(y_{m,j,s},\ldots ,y_{m,j,s+\delta } \}\) as the slack-window and the true positives \(\text {TP}_{i,m}\) as the number of snapshots, where \(x_{i,j,s}\) is one and \(\Delta _{y,j,s}(\delta )\) contains a one. Using this basic approach, we can calculate the true positive rate (TPR), the true negative rate (TNR), the accuracy (ACC), and the F1 score. In the results section, we report the mean and standard deviation over all annotators for each method and each metric at a slack of \(\delta =1\). We additionally calculated all tables from Section 5 using a slack of zero (\(\delta =0\)), resulting in the standard, more strict classification metrics. As expected, the performance scores of most methods are lower without slack. However, the deviations are mostly within small margins and the order of the three best results as well as the qualitative picture don’t change.
5. RESULTS
We calculated pairwise Cohen’s Kappa scores between each of the six annotations in order to evaluate annotator agreement. We obtained values between 0.55 and 0.8 with a mean of 0.7 which can be considered a moderate agreement. We expected different approaches from annotators based on preference. Therefore, we believe the moderate agreement values give sufficient support for the validity of the annotations. Additionally, we computed the mean agreement within study groups which is 0.7 for group one and 0.67 for group two. Since the agreement between the study groups is 0.7 as well, we cannot report any systematic group-dependent deviations in annotator agreement.
| Method | F1 | ACC | TPR | TNR |
|---|---|---|---|---|
| Completed line | .73 (.05) | .96 (.01) | .75 (.08) | .98 (.01) |
| Control-flow | .6 (.04) | .94 (.01) | .62 (.06) | .97 (.0) |
| \(pq\) state-space | .44 (.07) | .85 (.01) | .79 (.05) | .85 (.01) |
| Code-action | .56 (.05) | .94 (.02) | .50 (.1) | .98 (.0) |
| Pausing | .41 (.11) | .90 (.01) | .43 (.07) | .94 (.01) |
| Embedding | .35 (.02) | .90 (.03) | .34 (.03) | .95 (.01) |
| Execution traces | .34 (.04) | .93 (.02) | .23 (.05) | .99 (.0) |
| Levenshtein | .40 (.08) | .86 (.01) | .68 (.04) | .86 (.0) |
In Table 2, the results for the evaluation study are displayed. We can observe that all methods exhibit a relatively high accuracy. This can be explained by the class imbalance, with the negative class (no step) being highly prevalent with 92% over all annotations. In that light, only four out of eight methods outperform the trivial baseline (setting all snapshots to "no step"). Due to the class-imbalance, the F1 score is better suited for comparing the methods. The completed line method and the control-flow method perform best with 0.73 and 0.6 F1, respectively. Assigning steps when code-actions are taken also seems to partially align with annotator opinions (0.56 F1). The autoregressive distance-based methods using LLM embeddings (0.35 F1) and execution traces (0.34 F1) perform worse than the auto-regressive Levenshtein method (0.40 F1). The \(pq\) state-space and the pausing method both have a larger F1 (0.44 and 0.41).
| Method | F1 group 1 | F1 group 2 |
|---|---|---|
| Completed line | .76 (.03) | .70 (.05) |
| Control-flow | .64 (.02) | .59 (.05) |
| \(pq\) state-space | .51 (.03) | .39 (.05) |
| Code-action | .54 (.03) | .59 (.04) |
| Pausing | .48 (.03) | .34 (.11) |
| Embedding | .39 (.02) | .32 (.01) |
| Execution traces | .34 (.04) | .36 (.05) |
| Levenshtein | .48 (.02) | .35 (.06) |
Table 3 shows the F1 scores for the different sub-division methods by annotator experience. Group 1 refers to the three less experienced annotators with easier tasks; group 2 refers to the more experienced annotators with harder tasks. There is a clear trend towards a lower performance of the automatic trace sub-division methods for group 2. The worsening performance is most severe for the \(pq\)-state-space method with 0.51 F1 for group 1 vs. 0.39 F1 for group 2, but even the best-performing methods, completed line and control-flow, perform worse for group 2 with a difference of -0.06 and -0.05, respectively. By contrast, trace sub-division based on the code-actions in the UI (run, feedback request, submission) shows a performance increase of 0.06 for the second group.
5.1 Survey results
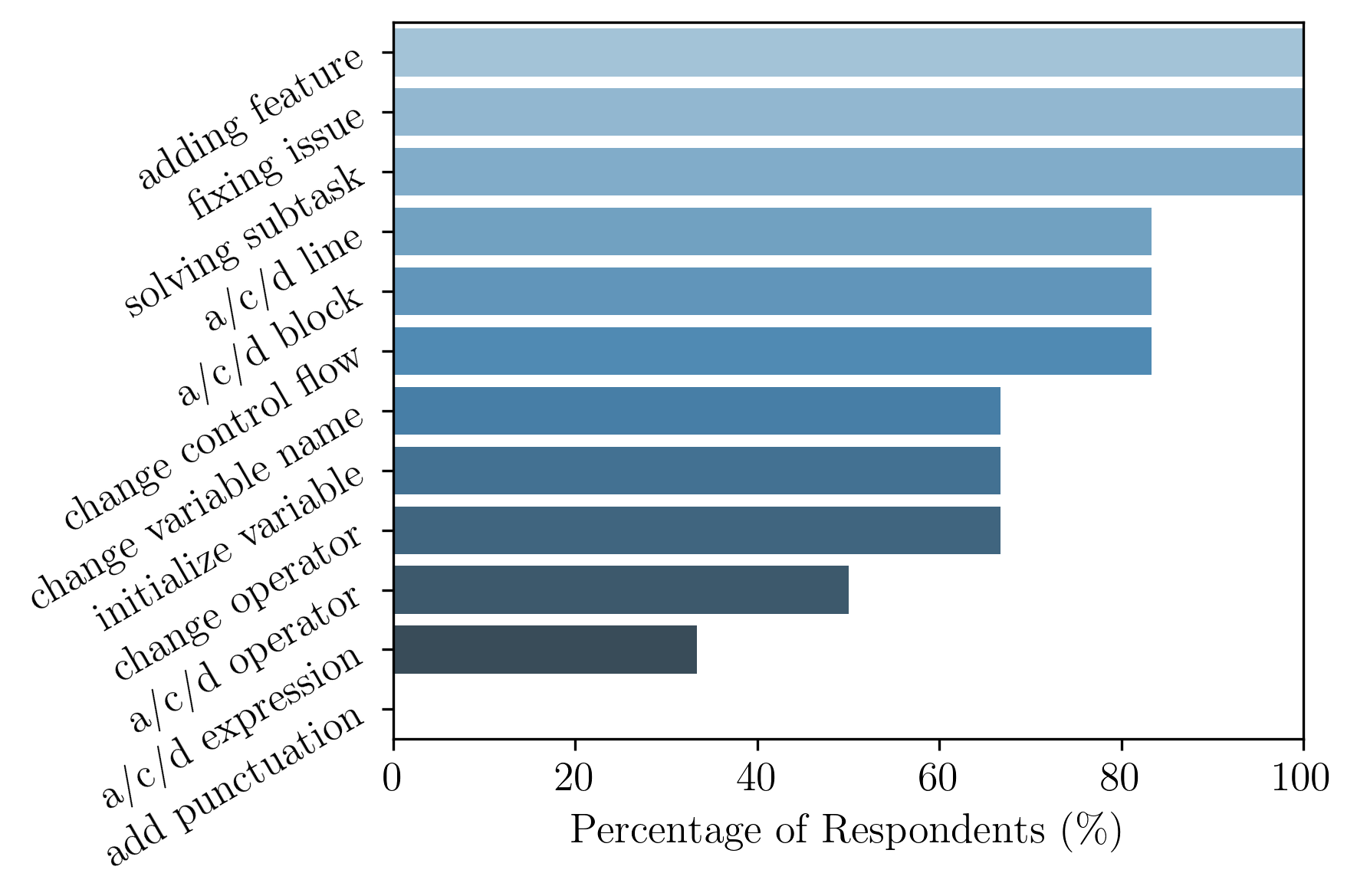
The bar plot in Figure 3 shows the percentage of annotators who self-report to have used a certain granularity for determining a step during the study. All granularities, except one (adding punctuation) where used by at least two of the annotators. 100% of annotators stated that they considered whether students were adding a feature, fixing an issue, or solving a sub-task at least once, respectively, for determining a step. Adding/deleting/changing lines or blocks and changing the control flow are also prominent with 83%.
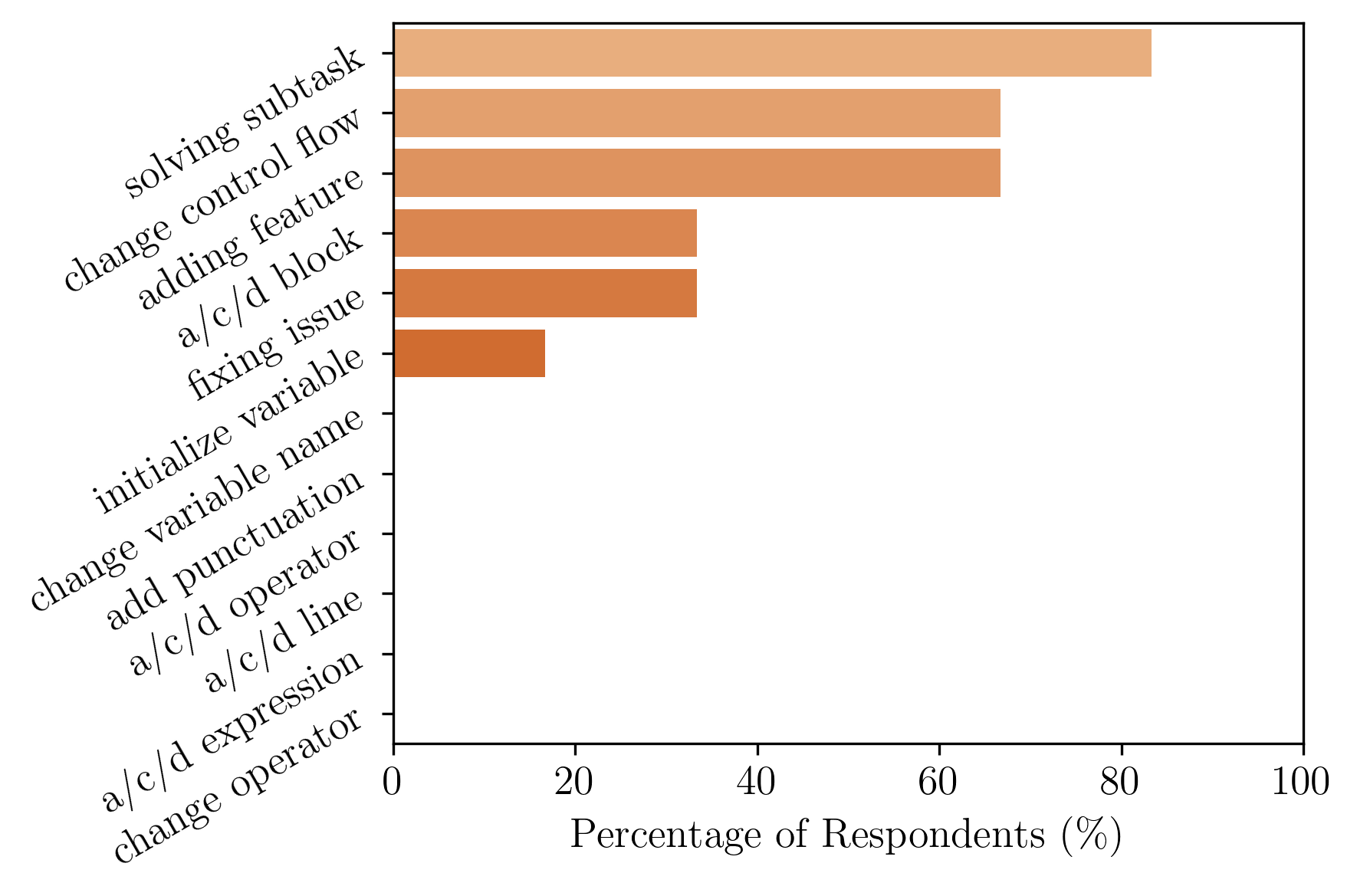
Figure 4 shows the percentage of annotators who considered a certain granularity among the 3 most important for determining steps. The solving of a subtask is among the most important indicators of a step for five out of six annotators. Changes of the control flow and adding features are also prominent with 66%. All other granularities achieved lower ratings. Interestingly, adding, changing or deleting lines was not mentioned by any of the annotators as among the top 3 most important indicators of a step—even though this granularity matches human annotations particularly well (see Table 2).
6. LIMITATIONS & CONCLUSION
Within this work, we have conducted a study to investigate what tutors and experienced students regard as steps in introductory Python tasks. Our study design differentiates two groups of annotators, who get tasks assigned based on experience. The selection of tutors and students as annotators and the task assignment based on difficulty/experience serve the purpose of aligning our approach with Vygostky’s learning theory, which suggests that next-step hints should be within the learners ZPD. We also have developed a novel tool for step annotation in programming traces. The system usability was evaluated by the annotators and scored highly, reassuring our impression that it serves the purpose of efficiently displaying and annotating programming traces. We compared human step annotations to different automatic trace sub-division methods extracted from cognitive science perspectives on programming and prior work on next-step hints. Steps based on completed lines showed the best alignment to the annotations. Strong results are also achieved at the level of the control-flow.
Several limitations arise due to the limited scope of this study. Firstly, we collected programming traces in only two university courses with a high degree of computer science students. Therefore, not all results may generalize to different course situations and populations. Furthermore, we have used Python as the only programming language for our studies, making the results dependent on Pythons specific features like dynamic typing. Additionally, the annotation guidelines provided to the annotators were supposed to only give minimal direction and a high degree of freedom to the annotators. However, the results might still be influenced by specific phrasings: for instance, we explicitly addressed assigning steps for fixing an issue, which also ranks relatively high in the post survey. Additionally, an issue appeared during the data collection: In three cases, the bonus set contained some duplicate tasks (duplicate annotations where omitted). Since the bonus set was solved after the main set, these remain unaffected.
Our results imply that simple rule-based methods can perform well at determining steps. This interpretation should be contextualized with our study parameters, though: the tasks in our study correspond to an introductory level and are relatively short. We hypothesize that our results could have differed for harder and longer tasks. This assumption is supported by the results of Table 3 which shows that the line-based approach performs worse for the more experienced group with harder tasks. On the contrary, the sub-division based on code-actions seems to work better for harder tasks, which might imply that the structure of steps is more complex. In the post-survey, the annotators favored annotating steps for more coarse, functionally driven granularities (e.g., adding a feature). For simple programming tasks such as the ones in our study, structural indicators like completed lines may co-incide with functional ones, but this may not hold for more complex programming tasks. Still, our results suggest that, for introductory Python programming, line completion is a strong indicator of steps. We do encourage researchers to use our open-sourced step annotation tool to investigate steps in other context. Future work in this research direction should also consider different programming languages, more complex tasks and additional sub-division methods that account for these scenarios. Practical applications of step sub-division methods according to the results of this paper should happen under careful evaluation on whether the obtained results are plausible and desirable for the task type at hand as otherwise, sub-optimal pedagogical results might be obtained.
7. ACKNOWLEDGMENTS
We gratefully acknowledge the support of the project “SAIL: SustAInable Lifecycle of Intelligent Socio-Technical Systems” project. SAIL is funded by the Ministry of Culture and Science of the State of North Rhine-Westphalia (Germany) (grant no. NW21-059A).
8. REFERENCES
- A. Bangor, P. T. Kortum, and J. T. Miller. An empirical evaluation of the system usability scale. International Journal of Human–Computer Interaction, 24(6):574–594, 2008.
- A. Birillo, E. Artser, A. Potriasaeva, I. Vlasov, K. Dzialets, Y. Golubev, I. Gerasimov, H. Keuning, and T. Bryksin. One step at a time: Combining llms and static analysis to generate next-step hints for programming tasks. In Proceedings of the 24th Koli Calling International Conference on Computing Education Research, New York, NY, USA, 2024.
- J. Dannath, A. Deriyeva, and B. Paaßen. Evaluating task-level struggle detection methods in intelligent tutoring systems for programming. In S. Schulz and N. Kiesler, editors, 22. Fachtagung Bildungstechnologien (DELFI), Fulda, Germany, 2024. Gesellschaft für Informatik e.V.
- A. Deriyeva, J. Dannath, and B. Paaßen. SCRIPT: Implementing an intelligent tutoring system for programming in a german university context. In C. Stracke, S. Sankaranarayanan, P. Chen, and E. Blanchard, editors, Proceedings of the 26th International Conference on Artificial Intelligence in Education (AIED 2025) Practitioner’s Track, Palermo, Italy, 2025. accepted.
- R. Duran, J. Sorva, and S. Leite. Towards an analysis of program complexity from a cognitive perspective. In Proceedings of the 2018 ACM Conference on International Computing Education Research, pages 21–30, Espoo Finland, 2018. ACM.
- F. Gobet. Chunking models of expertise: implications for education. Applied Cognitive Psychology, 19(2):183–204, 2005.
- J. Hammond and P. Gibbons. Putting scaffolding to work: The contribution of scaffolding in articulating ESL education. Prospect, 20(1):6–30, 2005.
- J. Jeuring, H. Keuning, S. Marwan, D. Bouvier, C. Izu, N. Kiesler, T. Lehtinen, D. Lohr, A. Petersen, and S. Sarsa. Steps learners take when solving programming tasks, and how learning environments (should) respond to them. In Proceedings of the 27th ACM Conference on on Innovation and Technology in Computer Science Education Vol. 2, pages 570–571, Dublin, Ireland, 2022. ACM.
- J. Jeuring, H. Keuning, S. Marwan, D. Bouvier, C. Izu, N. Kiesler, T. Lehtinen, D. Lohr, A. Peterson, and S. Sarsa. Towards giving timely formative feedback and hints to novice programmers. In Proceedings of the 2022 Working Group Reports on Innovation and Technology in Computer Science Education, pages 95–115, Dublin, Ireland, 2022. ACM.
- T. Jiang, S. Huang, Z. Luan, D. Wang, and F. Zhuang. Scaling sentence embeddings with large language models. In Findings of the Association for Computational Linguistics: EMNLP 2024, pages 3182–3196, Miami, Florida, USA, 2024.
- J. A. Kulik and J. Fletcher. Effectiveness of intelligent tutoring systems: a meta-analytic review. Review of educational research, 86(1):42–78, 2016.
- S. Marwan, Y. Shi, I. Menezes, M. Chi, T. Barnes, and T. W. Price. Just a few expert constraints can help: Humanizing data-driven subgoal detection for novice programming. In Proceedings of The 14th International Conference on Educational Data Mining, Paris, France, 2021.
- J. McBroom, I. Koprinska, and K. Yacef. A survey of automated programming hint generation: The hints framework. ACM Computing Surveys, 54(8):1–27, Oct. 2021.
- J. McBroom, B. Paaßen, B. Jeffries, I. Koprinska, and K. Yacef. Progress networks as a tool for analysing student programming difficulties. In Proceedings of the 23rd Australasian Computing Education Conference, pages 158–167, Virtual SA Australia, 2021. ACM.
- J. Mead, S. Gray, J. Hamer, R. James, J. Sorva, C. S. Clair, and L. Thomas. A cognitive approach to identifying measurable milestones for programming skill acquisition. In Working group reports on ITiCSE on Innovation and technology in computer science education - ITiCSE-WGR ’06, pages 182–194, Bologna, Italy, 2006. Association for Computing Machinery.
- B. Paaßen. Python programming dataset. https://doi.org/10.4119/unibi/2941052, 2019.
- B. Paaßen, J. Jensen, and B. Hammer. Execution traces as a powerful data representation for intelligent tutoring systems for programming. In Proceedings of the 9th International Conference on Educational Data Mining, Raleigh, North Carolina, 2016.
- T. W. Price, Y. Dong, and T. Barnes. Generating data-driven hints for open-ended programming. In Proceedings of the 9th International Conference on Educational Data Mining, Raleigh, North Carolina, 2016.
- T. W. Price, Y. Dong, R. Zhi, B. Paaßen, N. Lytle, V. Cateté, and T. Barnes. A comparison of the quality of data-driven programming hint generation algorithms. International Journal of Artificial Intelligence in Education, 29(3):368–395, 2019.
- L. Roest, H. Keuning, and J. Jeuring. Next-step hint generation for introductory programming using large language models. In Proceedings of the 26th Australasian Computing Education Conference, Sydney, Australia, 2024.
- B. Rozière, J. Gehring, F. Gloeckle, S. Sootla, I. Gat, X. Tan, Y. Adi, J. Liu, T. Remez, J. Rapin, A. Kozhevnikov, I. Evtimov, J. Bitton, M. P. Bhatt, C. C. Ferrer, A. Grattafiori, W. Xiong, A. D’efossez, J. Copet, F. Azhar, H. Touvron, L. Martin, N. Usunier, T. Scialom, and G. Synnaeve. Code llama: Open foundation models for code. ArXiv, abs/2308.12950, 2023.
- J. Sauro and J. R. Lewis. Chapter 8 - standardized usability questionnaires. In J. Sauro and J. R. Lewis, editors, Quantifying the User Experience (Second Edition), pages 185–248, Boston, 2016. Morgan Kaufmann.
- J. Urry and J. Edwards. A framework that explores the cognitive load of CS1 assignments using pausing behavior. In Proceedings of the 55th ACM Technical Symposium on Computer Science Education V. 1, pages 1347–1353, Portland OR USA, 2024. ACM.
- K. VanLehn. The relative effectiveness of human tutoring, intelligent tutoring systems, and other tutoring systems. Educational Psychologist, 46(4):197–221, 2011.
- L. S. Vygotsky. Mind in Society: Development of Higher Psychological Processes. Harvard University Press, Cambridge, Massachusetts, 1978.
- R. Zhi, T. W. Price, and N. Lytle. Reducing the state space of programming problems through data-driven feature detection. In Proceedings of the Educational Data Mining in Computer Science Education Workshop at the International Conference on Educational Data Mining, Buffalo, New York, 2018.
1https://gitlab.ub.uni-bielefeld.de/publications-ag-kml/programming-step-analysis
2https://gitlab.ub.uni-bielefeld.de/publications-ag-kml/step-annotation-tool
© 2025 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.