ABSTRACT

In educational systems, predictive models face significant challenges during initial deployment and when new students begin to use them or when new exercises are added to the system due to a lack of data for making initial inferences, often called the cold start problem. This paper tests logitdec and logitdecevol, "evolutionary" features within the Logistic Knowledge Tracing (LKT) framework. These features appear ideal to mitigate cold starts when there is very little data to train the model as well as when there is no prior data for the students and items. Logitdec, which is applied here to individual students, is a log-transformed running ratio that employs exponential decay to prioritize recent student performance. At the same time, logitdecevol is the same log-transformed ratio of successes and failures that uses prior observations for the knowledge component (KC) across all students. Evaluated on three datasets using temporal cross-validation, our results show that models composed with logitdec and logitdecevol outperform traditional methods (e.g., Additive Factors Model (AFM), Bayesian Knowledge Tracing (BKT), and Elo) in early prediction accuracy. The simplified 7-parameter LKT model outperformed alternatives with very little training data (e.g., hundreds of observations and fit better than alternatives even if they were trained on 10x more data. The proposed LKT model’s simplicity (4 regression coefficients, 3 nonlinear parameters to compute input features) ensures interpretability, computational efficiency, and generalizability, making it ideal for deployment in systems that use knowledge tracing to guide pedagogy.

Keywords

INTRODUCTION

In large-scale educational systems, a fundamental challenge is how to effectively model student performance when data are still sparse. This sparsity is especially problematic during deployment and for new students and items, as predictive models lack historical data for accurate assessments, leading to the “cold start” problem. Addressing this issue requires innovative approaches that can leverage limited information while minimizing the inaccuracies inherent to such early stages.

To consider models cold-start properties it is useful to define the taxonomy of knowledge tracing model cold starts. Table 1 shows these levels, which include global model parameters, student aptitude, and KC-specific difficulties. At the highest level, most, if not all, models tend to need coefficients, transition weights, link strength, or some other representation that allows the scaling of effects from the data into quantitative predictions about the future given this data. This involves adjusting model parameters such as coefficients or weights to align predictions with observed data trends. We call this level of cold start the global cold start problem.

Another level is the student's overall performance, which greatly helps a model capture prior knowledge and aptitude. A model can capture global averages but still do poorly with individual differences. Much prior research has investigated how student aptitude (e.g. [8]) can be estimated and even asked whether it is ethical to estimate some things based on characteristics such as race or gender. Some researchers argue that including demographic variables, such as race, in cold-start solutions risks amplifying systemic biases and overgeneralizing predictions due to sparse data [2]. They contend that such an approach may reinforce deterministic assumptions, like demographic destiny, and undermine trust in the system. Indeed, much prior work has involved inferring fixed values for each student (e.g. the Additive Factors Model (AFM)[3]), which only works as enough data is accumulated.

For example, recent work on csKT deep learning model attempts to mitigate the cold-start problem by introducing a kernel bias mechanism, which enhances the model's ability to generalize from short interaction sequences to longer ones [1]. Traditional knowledge tracing models struggle when student data is sparse, often leading to unreliable predictions early in the learning process. The kernel bias mechanism addresses this by penalizing attention weights based on sequence position, ensuring that the model prioritizes recent interactions while still retaining useful historical information. This approach not only improves predictive stability but also allows csKT to effectively handle growing student interaction sequences without suffering from performance degradation. We use a similar approach, but in the context of logistic regression.

Then there is the KC cold start issues, both between and within students. First, there is the cold start problem in the model's knowledge of the KC's difficulty levels across students. Typically, such values are used to seed predictions for new students, but they are only accurate if sufficient data is fit first. Typically, these values have been estimated after the fact with full knowledge of the data, which often leads to overfitting. While using a model with random effects is one solution [17], such models can be intractable for large student populations with many items, and tend to be slow regardless. In such cases, a better solution might be to use a process more akin to Bayesian updating, where skill difficulty is updated continuously based on each piece of new data that is recorded.

This KC-level issue has been solved in various ways in deep-learning KT models. The GSKPM [15], EAKT [7], and SINKT [6] models all address cold-start problems but focus on different aspects of KC modeling. EAKT relies on Large Language Models (LLMs) to estimate question-specific attributes like difficulty and ability requirements, dynamically adjusting these attributes with a Graph Attention Network to align with student cognitive characteristics. In contrast, GSKPM emphasizes leveraging graph-based relationships between KCs and knowledge domains through a two-stage hyper-aggregation process, incorporating local and global KC relationships for richer representations. SINKT also utilizes LLMs but focuses on generating semantic embeddings for questions rather than estimating explicit attributes, allowing it to better generalize to unseen KCs and questions. While EAKT enhances question-level feature learning and SINKT improves question representation through pre-trained embeddings, GSKPM uses structural relationships among KCs to mitigate sparsity and cold-start issues at a broader conceptual level. Each method improves predictive accuracy but differs in its reliance on either question-level features (EAKT, SINKT) or structural interdependencies (GSKPM). These solutions all involve new layers of complexity for model creation. In contrast, our solutions here are more traditional since they use the data itself to estimate KC and student knowledge efficiently.

The second of these KC cold start levels is the well-described cold start in understanding the student's proficiency with any KC over repetitions of this KC. Without any data for a student, there is no way to predict the performance of the student for a KC meaningfully except by using the global and between-student estimates described in the previous paragraphs. So, models have developed ways to track this change. The AFM model is the most basic example of this since it does not adapt to proficiency; rather, it only tracks the changes in performance due to learning. Other models like PFA and BKT are adaptive and result in predictions depending on performance. These models each are solutions to the cold start KC problem with students. Indeed, almost all modern knowledge tracing models are adaptive and designed to identify current performance for KC within students.

Solution for Cold-Starts in LKT (Logistic Knowledge Tracing)

We test an LKT feature that addresses these cold start problems in two forms: logitdec and logitdecevol. Logitdec at the student level has been introduced previously and compared with using fixed intercepts for fitting entire datasets [12]; however, it was not revealed in that work that it also greatly improves cold-start problems for new students. The logitdec feature operates within the Logistic Knowledge Tracing (LKT) framework and is designed to model the temporal relevance of past student interactions dynamically and adaptively. Specifically, it tracks a student's success and failure counts. Instead of treating all events equally, logitdec applies an exponential decay function to these counts so that more recent interactions are weighted more heavily than older ones. Consequently, if a student struggles early on but improves over time, the logitdec feature ensures that their most recent successes have the most influence on the model's prediction.

$$\text{Logitdec = }\log\left( \frac{1 \cdot d^{w} + \sum_{i = 1}^{w}v_{i} \cdot d^{w - i}}{1 \cdot d^{w} + \sum_{i = 1}^{w}\left( 1 - v_{i} \right) \cdot d^{w - i}} \right)$$

In this equation:

• Ghost Attempt: Add 1 ghost success in the numerator and 1 ghost failure in the denominator, ensuring the ratio never becomes undefined, while also resulting in an unbiased prediction of 0 when there is no data on the student. While ghost attempts could be varied as a parameter, we have never done this, primarily to maintain model simplicity. It also seems likely that adjustments in the global intercept, coefficient on the feature, and decay parameter are quite sufficient.
• Decay : Multiply each observation by $d^{w - i}$, giving more weight to recent events.
• Weighted Successes (Numerator): $1 \cdot d^{w} + \sum_{i = 1}^{w}v_{i} \cdot d^{w - i}$i, capturing both ghost and actual successes.
• Weighted Failures (Denominator): $1 \cdot d^{w} + \sum_{i = 1}^{w}\left( 1 - v_{i} \right) \cdot d^{w - i}$, capturing both ghost and actual failures.

To address the challenges posed by sparse data (or no data), logitdec incorporates "ghost" successes and failures, which add a baseline count of 1 to both decayed successes and failures. This smoothing mechanism prevents the feature from becoming undefined or overly skewed when very few interactions are available, as is common in cold-start scenarios. For instance, if a new student has only one or two interactions, the ghost values ensure that predictions remain stable and robust, mitigating the volatility that could arise from relying solely on raw, limited data. Ultimately, the number of ghost attempts could be another factor in this mechanism, we did not explore that here.

This mechanism shares conceptual similarities with the kernel bias used in csKT, a model designed specifically to handle the cold-start problem in knowledge tracing [1]. Both approaches dynamically adjust the relevance of past interactions, prioritizing the most pertinent data while discounting older, less relevant information. Kernel bias achieves this by introducing a logarithmic decay function into the attention mechanism of csKT, emphasizing the temporal distance between interactions. Similarly, logitdec's exponential decay function models the natural forgetting curve, capturing how the impact of prior successes and failures diminishes over time.

Our second investigational feature provides a theoretical solution to this cold-start problem by pooling information across the entire population of students. Rather than focusing solely on a single learner’s sequence of attempts, logitdecevol constructs an evolving, decay-weighted estimate of KC performance that potentially draws on every prior response from every student. This effectively allows new students to “inherit” informational priors from those who came before them, enabling the model to produce more stable and informed predictions immediately—even before the new student has produced a substantial performance history of their own.

Conceptually, logitdecevol can be viewed as a population-level, time-sensitive parameterization process. It acts as a running summary of the ecosystem’s knowledge state. Continuously aggregating and updating a log-odds measure of success weighted by temporal decay ensures that the most recent and relevant patterns in the entire dataset shape the feature estimates. Older data still matter, but their influence gradually fades, ensuring that the model’s evolving features remain representative of current conditions. This item-level calibration helps ensure that even a brand-new student who has made no prior attempts, is immediately placed within a well-informed reference frame. The model already has a sense of which items are generally more or less difficult, informed by the broad, evolving consensus of previous learners’ outcomes.

From a theoretical standpoint, logitdecevol thus embraces a collective knowledge modeling perspective. Its emphasis on decayed, population-wide data allows it to handle cold start situations gracefully. Instead of starting from scratch each time a new student arrives, the model leverages the continuously updated population knowledge state to provide immediate, contextually informed predictions.

Methods

Datasets

We chose 3 datasets that were moderately large (large enough to show stable fit) and that varied in types of practice. Only the first attempts at each step were retained to ensure a clean learning trajectory. Where applicable, records missing KC assignments were removed, and spacing predictors were computed to capture recency. Full project code is available at: https://github.com/Optimal-Learning-Lab/EDM-2025.

Cloze Practice Data

The statistics cloze dataset included 58,316 observations from 478 participants who learned statistical concepts by reading sentences and filling in missing words. Participants were adults recruited from Amazon Mechanical Turk. There were 72 KCs in the dataset, derived from 18 sentences, each with one of four possible words missing (cloze items). The number of times specific cloze items were presented and the temporal spacing between presentations (narrow, medium, or wide) was manipulated. The post-practice test (filling in missing words) could be after two minutes, one day, or three days (manipulated between students). Data is available at https://pslcdatashop.web.cmu.edu/DatasetInfo?datasetId=5513.

Blocked vs Interleaved Instruction Data

The dataset from Experiment 1 of Patel et al. (2016) includes 22,195 transactions from 70 sixth-grade students in a Pittsburgh-area school. Students interacted with an online intelligent tutoring system for fraction arithmetic, specifically fraction addition and fraction multiplication. We used student identifiers (Anon.Student.Id) and KC identifiers (KC..Field.), and step-level correctness data as key variables. There were 16 KC coded by the original investigators. The dataset captures stepwise student responses, including correctness feedback, hint requests, and problem-solving strategies. The problems involved fraction addition with and without common denominators and fraction multiplication, allowing analysis of error patterns and learning trajectories. Data is available at https://pslcdatashop.web.cmu.edu/DatasetInfo?datasetId=1706.

Mathia Data

The MATHia dataset included 119,379 transactions from 500 students from the unit Modeling Two-Step Expressions for the 2019-2020 school year. We used the student (Anon.Student.Id), MATHia assigned skills (KC..MATHia.). There were nine KCs coded in the dataset. For simplicity, we chose not to use the unique steps as an item in our models. This dataset included skills such as “write expression negative slope” and “enter given, reading numerals”. Data at https://pslcdatashop.web.cmu.edu/DatasetInfo?datasetId=4845.

Models

LKT variants

There is no canonical logistic knowledge tracing (LKT) model, since it is a framework, not a specific model. For the LKT models we tested, each model name represents a combination of features used in logistic regression to predict student performance. These features encode various aspects of student learning history, KCs, and temporal dependencies. Here are the features we used in the following model comparisons:

• $\text{int}_{S}$ (Student Intercept). This feature assigns an individual intercept to each student using one-hot encoding. This means that each student has a unique baseline effect, capturing differences in their overall ability or learning style.
• $\text{int}_{KC}$ (KC Intercept). This feature assigns a unique intercept to each KC. It accounts for the inherent difficulty of different skills or concepts, ensuring that harder KCs have appropriately lower baseline probabilities.
• $\text{lineafm\$}$ (Additive Factors Feature for KCs). This feature models student learning by tracking the number of prior practice encounters with each KC. It assumes a logistic relationship between the count of prior attempts on a KC and the probability of success, allowing us to quantify learning gains from repeated practice.
• $\text{logitdec}$ (Logit-Based Success/Failure Decay for Students). Described previously. We set d to .98, which tends to be a good default, since it results in the trailing window having enough stability to consistently track performance while still adjusting relative rapidly. We could have conceivably optimized this parameter but with the 90 fits across multiple models we were concerned the nonlinear optimizations for this parameter would be slow and provide little additional gain.
• $\text{Logitdecevol}$(Logit-Based Success/Failure Decay for KCs). Described previously. We set d to .98.
• $\text{recency}$ (Time Decay of Prior Practice Effects). This feature models how the passage of time affects retention, using a power-law decay function of seconds in the past. The idea is that more recent interactions should have a stronger impact on performance predictions, reflecting the well-established forgetting curve. We set d to .25.
• $\text{logsuc}$ (Success-Only Practice Feature). The natural log of 1 + the prior success. This feature is similar to lineafm but only considers past successes when counting prior practice attempts. The natural log causes decreasing marginal returns.

Interpreting Model Combinations

Each logistic regression model combines different features to predict student outcomes. For example, our 1^st model, the base AFM model structure:

$$int_{S} + int_{KC} + lineaf{m\$}_{KC}$$

Uses intercepts for students and KCs, with a linear effect of prior attempts on the logit score used to compute the logistic regression probability. In the version, all the parameters are optimized as fixed effects, which can make a model less generalizable due to overfitting problems inherent in this model [17]. While using random effects could be one solution, random effects tend to be unreliable as data gets larger, precluding them practically [5]. The $ indicates that each KC has its own coefficient to describe practice attempts.

Our 2^nd model is a test of whether logitdec can replace the fixed student intercept:

$$logitdec_{S} + int_{KC} + lineaf{m\$}_{KC}$$

Our 3^rd model is a test of whether logitdecevol can replace the fixed KC intercept:

$$int_{S} + logitdecevol_{KC} + lineaf{m\$}_{KC}$$

Our 4^th model replaces both intercepts with our new features, including decayed success/failure for both students and KCs across students, creating a more adaptive learning model.

$$logitdec_{S} + logitdecevol_{KC} + lineaf{m\$}_{KC}$$

Our 5^th model takes the 4^th model and replaces the lineafm (tracking all opportunities) with linesuc (tracking successes for a KC) from the performance factors analysis logistic regression model [11]. Also, rather than assuming each KC has a different logsuc slope, we assumed a single coefficient characterizing all KC learning curves. Logsuc is implicitly adaptive since it only increases predictions following success, causing it to gain more quickly for easy KCs and known KCs

$$logitdec_{S} + logitdecevol_{KC} + {logsuc}_{KC}$$

Our 6^th model adds time-based forgetting, capturing how recency of the KC affects student performance.

$$logitdec_{S} + logitdecevol_{KC} + {logsuc}_{KC} + recency_{KC}$$

BKT

Bayesian Knowledge Tracing (BKT) is a widely used algorithm in intelligent tutoring systems to model a student's mastery of specific skills over time. It employs a Hidden Markov Model (HMM) framework [4], where the hidden states represent whether a student has mastered a particular skill, and the observable outputs correspond to the correctness of the student's responses. The model operates under the assumption that each skill is either mastered or not, and that student responses are binary—correct or incorrect.

Four key parameters define the BKT model:

• Initial Knowledge $\text{(}p\left( L_{0} \right)\text{)}$: The probability that a student knows the skill prior to any practice.
• Learning Rate $\text{(}p(T)\text{)}$: The probability that a student will learn the skill after an opportunity to apply it.
• Slip $\text{(}p(S)\text{)}$: The probability that a student makes a mistake when applying a known skill.
• Guess $\text{(}p(G)\text{)}$: The probability that a student correctly applies a skill despite not having mastered it.

These parameters are used to update the probability that a student has mastered a skill after each practice opportunity. To implement BKT efficiently on large datasets, we utilized the `hmm-scalable` package, a command-line utility designed for fitting Hidden Markov Models at scale. This tool is particularly suited for educational data mining applications. We used the following settings:

• -s 1.3.1: Skill structure (classical BKT) with Conjugate Gradient Descent and Hestenes-Stiefel formula.
• -m 1: Provide metrics AIC, BIC, RMSE
• -p 1: Report model predictions on the train.
• -e 0.0000001: Defines the convergence threshold for the Expectation-Maximization algorithm.
• -i 1000: Sets the maximum number of iterations for parameter estimation.

Standard ELO

The Elo rating system, originally devised to estimate players’ abilities in games, has also been used to estimate student performance [13, 16]. Elo updates skill estimates based on the difference between its predictions and actual outcomes. For instance, to update player i estimate, the difference between the model prediction P(R=1) and the actual result R is multiplied by hyperparameter K. The value of K controls the rate of the estimate change. For example, with K = .2, if a student answered correctly (R = 1) and the model prediction P(R = 1) was .6, the update to $\theta i\$would be +.08.

$$\theta i\,\, = \,\theta i\, + \, K\left( R\, - \, P(R\, = \, 1) \right)$$

Elo has been shown to perform comparably to alternatives previously [14]. The small number of parameters offers a potential advantage when it comes to cold start situations, it only has one hyperparameter to estimate. Elo can estimate student skill as well as skill and item difficulties, and these estimates update as data accumulates. However, in the present work Elo only estimated student-level and KC-level parameters. The simplicity and elegance of Elo offers a strong baseline when it comes to evaluating knowledge tracing models. A potential disadvantage of Elo is that it does not account for other aspects of performance such as temporal recency, spacing, or the amount of practice. In the present work, the Elo model estimated student and item parameters.

Temporal Cross Validation

For the analysis depicted in Figure 1, we employed a rolling (i.e., forward chaining) cross-validation method to properly account for the temporal ordering of the data. Specifically, we begin by ordering our dataset by time and subsequently split it into 100 folds, fold 1 first, fold 2 next, etc., and then sequentially expand the training set with each iteration of the cross-validation—using folds 1,…,i to train and then validated on the subsequent 70 folds (i+1),…,(i+70). As seen in the figures, the fit stabilizes well before 30% of the data is observed, this allowed us to validate with 70% of the data for each of the 30 iterations (for comparability). For the Elo model, the training folds were for estimating the K hyperparameter.

Results

In Figure 1, we see that the logitdec and logitdecevol perform excellently across all 3 datasets. Models with evolutionary features improved faster and with meaningfully less data than alternatives. For example, with just 2% of the dataset, an evolutionary feature model outperformed BKT or Elo regardless of how much data they were trained on. The first LKT model, AFM, was the poorest fit across the datasets, even when significant data is accumulated. This indicates that the evolutionary features performed better in each case than the fixed intercepts despite drastically fewer parameters (just 2 for each term rather than the n of the KCs). However, by contrasting the separate addition of logitdec and logitdecevol to AFM, we can see that the logitdec at the student level provides a much larger gain. Indeed, when logitdec is present with logitdecevol, there seems to be some indication that there is no additional advantage of logitdecevol. Finally, we see that the addition of logsuc results in the model producing the best cold-starting performance and dominating the other model across datasets.

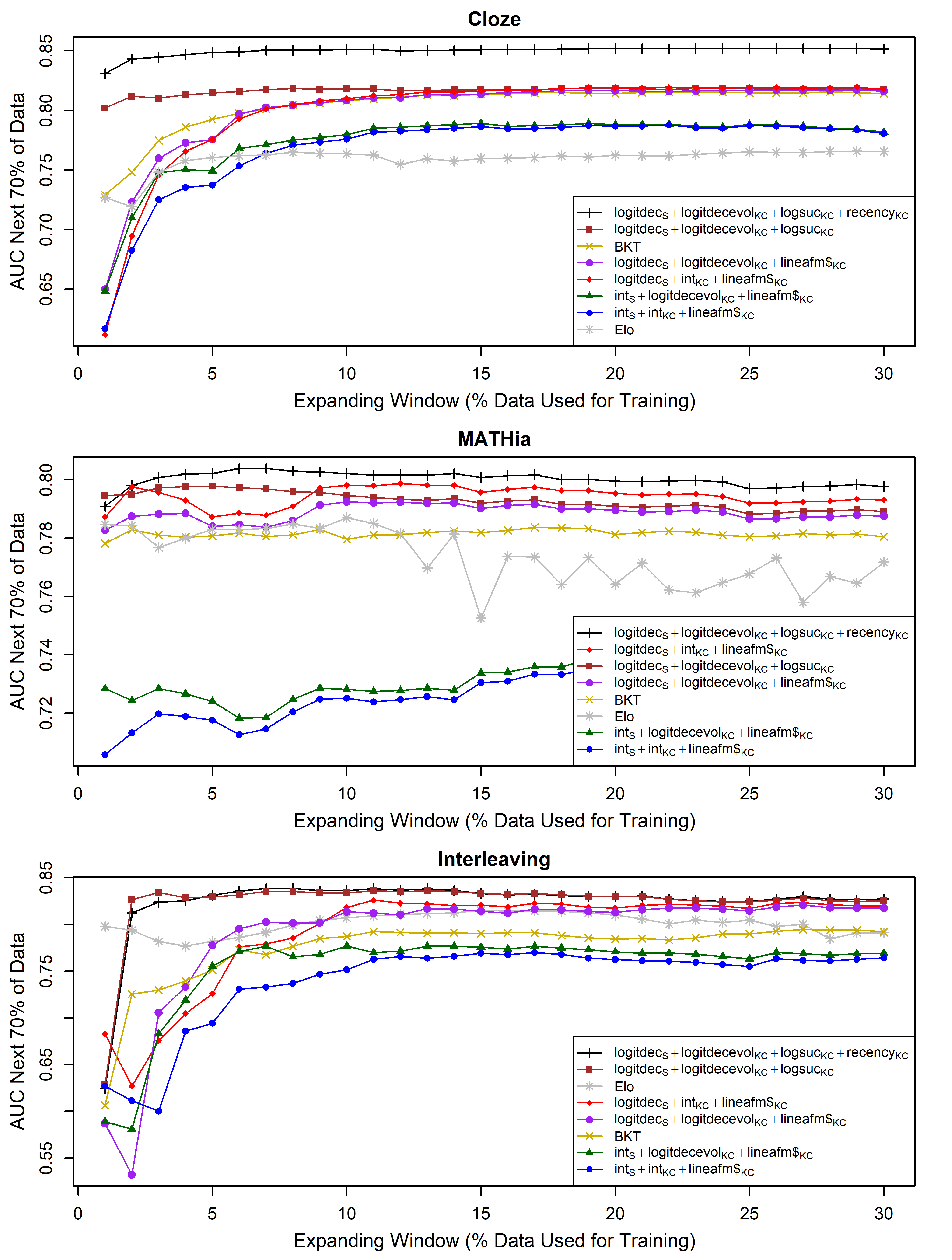
Patterns in Figure 1 for BKT and Elo were interesting. Both proved to fit better than AFM and have some relative advantages for the cold start problem. Elo, in particular, shows flat performance, showing that a minimum size of 1% of data was already adequate for our datasets. Neither model, however, worked as well as the models with the logsuc feature.

To compare the parameter estimates between logitdecevol and Elo, the scaled final values generated in the dataset were compared between the LKT model with logitdecevol for KCs and logitdec for students and the Elo model parameter estimates for KCs and Student. As can be seen in Figure 4, the values were quite similar. Student-level and skill-level estimates from the two models were highly correlated (see Table 2).

Discussion

In all datasets, LKT models with the proposed features outperformed alternatives and were at or near peak accuracy with less than 5% of the data. Other models frequently required considerably more data to reach their peak accuracy. The success of the LKT model in addressing cold-start challenges stems from its deliberate simplicity, which carries implications for both theoretical research and practical implementation in adaptive learning systems. With only four coefficients and three nonlinear parameters—such as the decay factor d and the ghost attempt weighting—the model achieves a rare balance between the predictive accuracy of larger LKT models [10] and the computational frugality of Elo. These new features included within the LKT framework share many of the advantages of the Elo approach to ability and difficulty estimation but allow for the simple integration of additional features such as recency and counts of successes and failures.

Logitdecevol performs somewhat weaker on MATHia, especially compared to a simpler model that includes only student logitdec parameters and KC intercepts. This may be due to the small number of KCs, which allows stable parameter estimation from smaller data segments. Notably, models using student intercepts perform poorly, indicating that MATHia students exhibit fluctuating baseline proficiency. These performance shifts are better captured by models that allow dynamic, rather than fixed, estimates of student ability.

This computational efficiency is paired with transparency. Each parameter in LKT maps directly to interpretable constructs: logitdec estimates a student's prior knowledge and aptitude, logitdecevol measures the difficulty of the items, and the recency factor quantifies the diminishing influence of the most recent past interaction to capture changes due to time between practices, while the logsuc feature captures the student's total history of success for a KC. Educators or system administrators can audit predictions without specialized expertise—for example, identifying that a student’s 70% success probability reflects a lack of recent practice and a KC’s moderately high difficulty for their recent practice experiences. This contrasts sharply with "black-box" approaches like deep knowledge tracing, where decisions are opaque, and auditing requires technical proficiency. The model’s simplicity also reduces ethical risks; systemic differences in KC difficulty estimates can be traced to instructional gaps rather than opaque algorithmic processes, aligning with calls for accountable AI in education [9].

Logitdec features are also comparable to Elo parameters (e.g., Figure 4). The adaptive nature of the logitdec features behaves quite similarly to Elo. Thus, an LKT model with logitdec features may offer the adaptivity and usefulness of Elo features (e.g., reporting skill-level proficiency), with the potential benefit of additional features like recency for improving model prediction accuracy.

Theoretically, LKT challenges the assumption that cold-start solutions necessitate architectural complexity. Its performance suggests that temporal decay mechanisms and population-level priors can compensate for sparse data more effectively than layered neural networks in early interaction regimes [10]. However, the model’s simplicity imposes tradeoffs: fixed decay rates overlook individual or domain-specific differences in forgetting, and it does not explicitly model prerequisite relationships between KCs, unlike graph-based approaches such as GSKPM [15].

Limitations & Future Directions

Our results are limited because we did not include deep knowledge tracing approaches in our comparison. This is a promising avenue for future research. For example, it is useful to contrast csKT and LKT, csKT is a deep learning model that addresses cold-start issues primarily at the student and KC levels—it trains on many short interaction sequences using kernel bias and cone attention to capture nuanced hierarchical and positional relationships. However, to learn these complex representations, csKT requires a globally trained model on a large dataset (thousands of short interaction sequences aggregated from many students). Short sequences between 50 and 100 interactions each were used. In contrast, the LKT model solves the global cold-start issue by leveraging evolutionary features like logitdec and logitdecevol to allow for a model with only a handful of parameters (7). The LKT features dynamically integrate individual student and population-level information, allowing the model to perform well globally even with only 1–2% of the data (around 1,000 interactions total across all students).

Conclusions

A resource-constrained edtech startup building a middle school math platform could deploy the LKT model with logitdec/logitdecevol to achieve immediate personalization without costly infrastructure. The model’s efficiency, training on just 1,000–2,000 interactions, streamlines onboarding for new students/teachers and enables real-time adjustments through weekly updates. By avoiding complex deep learning infrastructure, the team prioritizes pedagogical design over computational overhead. As the user base grows, the system’s transparency allows educators to audit predictions (e.g., tracing a 65% success probability to low recent practice frequency), fostering trust with school partners. This lean approach aligns with rapid iteration goals, proving that ethical, adaptive AI need not require massive data or engineering resources.

LKT demonstrates that cold-start challenges can be addressed through parsimonious design rather than computational brute force. Its efficiency, transparency, and ease of deployment make it particularly suited for resource-constrained settings. By prioritizing interpretability and accessibility, the model advances the goal of ethical, scalable, adaptive learning systems that empower—rather than overshadow—educators and learners.

ACKNOWLEDGMENTS

The work presented here was supported by the National Science Foundation under Grant No. 2301130.

REFERENCES

1. Bai, Y., Li, X., Liu, Z., Huang, Y., Guo, T., Hou, M., Xia, F., and Luo, W., 2024. csKT: Addressing cold-start problem in knowledge tracing via kernel bias and cone attention. Expert Systems with Applications(2024/12/06/), 125988. DOI= http://dx.doi.org/10.1016/j.eswa.2024.125988.
2. Baker, R.S., Esbenshade, L., Vitale, J., and Karumbaiah, S., 2023. Using Demographic Data as Predictor Variables: A Questionable Choice. Journal of Educational Data Mining 15, 2, 22-52.
3. Cen, H., Koedinger, K., and Junker, B., 2006. Learning Factors Analysis: A General Method for Cognitive Model Evaluation and Improvement. In International Conference on Intelligent Tutoring Systems, M. Ikeda, K.D. Ashley and T.-W. Chan Eds. Springer, Jhongli, Taiwan, 164-176.
4. Corbett, A.T. and Anderson, J.R., 1994. Knowledge tracing: Modeling the acquisition of procedural knowledge. User Modeling and User-Adapted Interaction 4, 4 (1994), 253–278. DOI= http://dx.doi.org/10.1007/BF01099821.
5. DataShop Website, 2025.
6. Fu, L., Guan, H., Du, K., Lin, J., Xia, W., Zhang, W., Tang, R., Wang, Y., and Yu, Y., 2024. SINKT: A Structure-Aware Inductive Knowledge Tracing Model with Large Language Model. In (October 2024), 632--642.
7. Guo, Y., Shen, S., Liu, Q., Huang, Z., Zhu, L., Su, Y., and Chen, E., 2024. Mitigating Cold-Start Problems in Knowledge Tracing with Large Language Models: An Attribute-aware Approach. In Proceedings of the Proceedings of the 33rd ACM International Conference on Information and Knowledge Management (Boise, ID, USA2024), Association for Computing Machinery, 727–736. DOI= http://dx.doi.org/10.1145/3627673.3679664.
8. Liu, R. and Koedinger, K.R., 2017. Towards Reliable and Valid Measurement of Individualized Student Parameters. International Educational Data Mining Society.
9. Memarian, B. and Doleck, T., 2023. Fairness, Accountability, Transparency, and Ethics (FATE) in Artificial Intelligence (AI) and higher education: A systematic review. Computers and Education: Artificial Intelligence 5(2023/01/01/), 100152. DOI= http://dx.doi.org/10.1016/j.caeai.2023.100152.
10. Pavlik Jr, P.I. and Eglington, L.G., 2023. Automated Search Improves Logistic Knowledge Tracing, Surpassing Deep Learning in Accuracy and Explainability. Journal of Educational Data Mining 15, 3 (12/26), 58-86. DOI= http://dx.doi.org/10.5281/zenodo.10363337.
11. Pavlik Jr., P.I., Cen, H., and Koedinger, K.R., 2009. Performance factors analysis -- A new alternative to knowledge tracing. In Proceedings of the 14th International Conference on Artificial Intelligence in Education, V. Dimitrova, R. Mizoguchi, B.D. Boulay and A. Graesser Eds. IOS Press, Brighton, England, 531–538. DOI= http://dx.doi.org/10.3233/978-1-60750-028-5-531.
12. Pavlik, P.I., Eglington, L.G., and Harrell-Williams, L.M., 2021. Logistic Knowledge Tracing: A Constrained Framework for Learner Modeling. IEEE Transactions on Learning Technologies 14, 5, 624-639. DOI= http://dx.doi.org/10.1109/TLT.2021.3128569.
13. Pelánek, R., 2016. Applications of the Elo rating system in adaptive educational systems. Computers & Education 98(2016/07/01/), 169-179. DOI= http://dx.doi.org/10.1016/j.compedu.2016.03.017.
14. Scruggs, R., Baker, R.S., Pavlik, P.I., McLaren, B.M., and Liu, Z., 2023. How well do contemporary knowledge tracing algorithms predict the knowledge carried out of a digital learning game? Educational Technology Research and Development 71, 901-918. DOI= http://dx.doi.org/10.1007/s11423-023-10218-z.
15. Wu, J., Zhang, H., Huang, Z., Ding, L., Liu, Q., Sha, J., Chen, E., and Wang, S., 2024. Graph-based Student Knowledge Profile for Online Intelligent Education. In Proceedings of the 2024 SIAM International Conference on Data Mining (SDM) Society for Industrial and Applied Mathematics, 379-387. DOI= http://dx.doi.org/10.1137/1.9781611978032.43.
16. Yudelson, M., 2021. Individualization of Bayesian Knowledge Tracing Through Elo-infusion. In Artificial Intelligence in Education, I. Roll, D. Mcnamara, S. Sosnovsky, R. Luckin and V. Dimitrova Eds. Springer International Publishing, Cham, 412-416.
17. Yudelson, M., Pavlik Jr., P.I., and Koedinger, K.R., 2011. User Modeling – A Notoriously Black Art. In User Modeling, Adaption and Personalization, J. Konstan, R. Conejo, J. Marzo and N. Oliver Eds. Springer Berlin / Heidelberg, 317-328. DOI= http://dx.doi.org/10.1007/978-3-642-22362-4_27.

© 2025 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.