ABSTRACT
Feedback effectively supports STEM learning. Past work usually compared learning gains when estimating the effectiveness of different feedback types. Learning rates, in contrast, quantify learning from individual instructional feedback events, which may confirm or challenge existing scientific knowledge about feedback. We study how feedback types and prior knowledge, as a common moderator of feedback effectiveness, influence learning rate. Log data from N=61 incoming first-year university students working with StoichTutor, a tutoring system for chemistry, are analyzed. A total of 1,169 feedback messages are manually categorized using a coding scheme informed by literature. We use instructional factors analysis (IFA) to assess the relation between feedback types and learning rate across students with low and high prior knowledge. Correctness feedback significantly improved the learning rate for all students. In contrast, indirect and next-step feedback had negative impact on learning rates. We discuss how next-step feedback, which provides learners with an explanation of the problem or next step without a prior mistake been made, is likely too unspecific (low prior knowledge) or redundant (high prior knowledge) for learners to be effective. To the best of our knowledge, our study is the first to model feedback-specific learning rates using IFA.
Keywords
1. INTRODUCTION
Intelligent tutoring systems adapt content to learners by enabling step-by-step problem solving with feedback and hints [1, 48]. We studied StoichTutor [37], which supports learners in solving stoichiometry problems and provides different types of feedback. Stoichiometry deals with the quantitative relationships between reactants and products in chemical reactions [39]. Stoichiometry challenges learners, especially by linking mathematical and conceptual knowledge [7, 36]. We define feedback as highlighting differences between problem-solving step attempts and correct solutions and, optionally, providing error-specific instruction [20, 23]. Prior research has predicted that different feedback types have different impact on student learning during problem solving [20, 44, 18, 35]. In StoichTutor, these steps are associated with unique feedback events, which allows us to study how feedback events contribute to student learning rate.
Learning rate modeling quantifies the effectiveness of learning opportunities (e.g., completing a single problem-solving step and receiving accuracy feedback). Problem-solving steps are defined as the necessary actions required to solve the problem [48]. Learning rates represent how much a student’s performance improves with each additional opportunity to apply a specific skill [27]. In contrast, learning gain reflects the total performance improvement over an instructional period, capturing the difference between a student’s initial and final level of content mastery. It is challenging to attribute learning differences to distinct feedback events when an instructional system features multiple types of feedback. To address this challenge, we used instructional factors analysis (IFA), an extension of learning rate modeling, which estimates separate learning rates attributable to distinct types of instruction, for instance, feedback [12], a method commonly used in educational data mining (EDM) [5, 16]. IFA allows for an estimation of the impact of individual feedback events on learning [12]. Little past research has studied feedback at the process level by comparing feedback types. Exceptions only predicted overall performance [22] or have classified students’ perception of feedback [24] as opposed to studying how effective different feedback types are for learning rate. For example, prior work has examined self-explanation compared to giving explanations [12]. A similar method, called learning decomposition, is also concerned with estimating what instructional events contribute to efficient learning, but has only been applied to general tutor help during learning, as opposed to different types of feedback [3]. To the best of our knowledge, the impact of specific feedback on students’ learning rate has not yet been investigated. Hence, we ask:
RQ1: How do different feedback types in a tutoring system affect learning rate when solving stoichiometry problems?
We also studied how feedback effectiveness depends on students’ prior knowledge. Previous work has shown that learners with low prior knowledge benefit significantly from explanatory feedback [18, 46], while learners with a high level of prior knowledge are more likely to benefit from receiving less feedback [18]. In both cases, the term benefit refers primarily to pre-post learning gains. For instance, Fyfe et al. [18] found that learners with low prior knowledge improved their procedural knowledge more when provided with feedback during exploratory problem solving, while learners with higher prior knowledge performed better when feedback was withheld. Similarly, Sychev et al. [46] reported that students with lower initial comprehension levels showed greater learning gains after interacting with explanatory feedback in an intelligent tutoring system. Separately estimating IFA by prior knowledge learner groups, we ask:
RQ2: How do different types of feedback affect the rate of learning according to prior knowledge?
2. BACKGROUND
2.1 Feedback in Tutoring Systems
Feedback supports learners in reflecting on their performance, correcting mistakes, and improving strategies [44]. In tutoring systems, immediate feedback is provided in real time, supporting learning [13]. Current literature distinguish between two main types of feedback: corrective feedback and knowledge-of-results feedback. Whereas corrective feedback highlights errors and provides specific opportunities for correction such as explanations for error remediation, knowledge-of-results feedback simply indicates whether a response is right or wrong[20, 44, 43]. Corrective feedback can take many forms, such as a) explicit correction (an error is indicated and directly corrected) [34], b) indirect feedback (an error is hinted at, but the solution is not directly provided) [8], and c) elicitation and metalinguistic feedback (targeted questions and hints are used to draw attention to a mistake without providing the direct answer) [34]. These types of feedback are all common in tutoring systems and may have different impacts on learning. For example, corrective feedback in tutoring systems can contribute to the development of problem-solving strategies [44, 48]. However, to the best of our knowledge, no prior work has modeled learning rates of these distinct feedback types in tutoring systems.
2.2 Feedback Depending on Prior Knowledge
The effectiveness of feedback depends on learners’ prior knowledge [18, 35]. In a study on exploratory learning, learners with low prior knowledge benefited significantly more from feedback on the correct solution strategy, as it helped them gain procedural understanding and avoid misunderstandings [18]. In contrast, learners with higher prior knowledge sometimes benefited more from not receiving feedback on the correct solution strategy and exploring the learning environment without feedback, as the necessary schemata for solving the task are already available in working memory [18, 45]. Hence, research suggests that feedback should be adapted for learners, high prior knowledge learners tend to use several cognitive and metacognitive strategies [47].
These lines of research predicted differential effectiveness of feedback for learning. Learners with low prior knowledge in particular may benefit from tutoring systems that provide explanatory feedback and promote the avoidance of misunderstandings [21, 46]. In addition, knowledge-of-results feedback, as feedback on success and failure, may have a positive effect on learning[38]. A previous study on processing vector math in a computer system demonstrated that merely providing the correct answer (informing the learner of the correct solution) did not lead to learning gains for learners with low prior knowledge [21]. This aspect aligns with meta-analytic findings in the literature suggesting that feedback becomes increasingly effective with the inclusion of more detailed information, such as error descriptions or even instructions for subsequent steps. Furthermore, the effectiveness of corrective feedback is known to be influenced by variables such as competence in a specific content domain [50]. It is an open question to what extent different types of feedback in a tutoring system have a positive or negative effect on learning rate with different prior knowledge.
3. METHODS
3.1 Dataset Description
This study analyzed StoichTutors [37] log data to examine the impact of different types of feedback on student learning rates. The data set was collected in March and September 2023 from 61 incoming undergraduate students enrolled in a preparatory chemistry course for science students, solving up to seven stoichiometry problems. The preparatory chemistry course was designed for STEM students and introduced concepts of general chemistry that are required for studies in the natural sciences. This included teaching students how to solve stoichiometry problems. The course was structured according to the blended learning model, allowing learners to engage with exercises at their own pace in a digital learning environment as well as participate in face-to-face chemistry exercises both in the lecture hall and from their homes. During this two-week course, which included 6 days in presence, participants spent one hour working with StoichTutor, which was not incorporated as a standard learning tool in the preparatory course. Informed consent was obtained from all participants. Interactions in StoichTutor were logged to DataShop [29]. The dataset included problem-solving transactions where students attempted steps, received feedback, and were evaluated on correctness. After each problem-solving step, learners immediately received feedback, the impact of which was modeled in terms of the probability of entering a correct solution in subsequent problem-solving steps. This allowed for quantifying the distinct impact of these instructional events on learning [11], as opposed to the impact on other instructional differences (e.g., self-paced study, lectures) happening during the study’s practice period, or student-level differences in preparatory activity in-between the practice period and any assessments. As is common practice in EDM, we only retained first-attempt responses per step, thereby isolating students’ initial understanding prior to any further scaffolding or trial-and-error adjustments [10, 12], which yielded a total of 3,670 unique problem-solving step completions. We used StoichTutor’s standard knowledge component model for learning rate modeling [37]. This model included 44 skills.
Each problem-solving attempt was linked to a feedback type, so that the impact of feedback on learning rate could be modeled. To analyze the influence of prior knowledge, participants were divided into high and low prior knowledge groups based on their overall performance on a pre-test, using a median split. Each group’s average pre-test score was about 1.25 \(SD\) apart from one another, indicating satisfactory variation in prior knowledge.
3.2 Feedback in StoichTutor
3.2.1 Feedback Categorization in StoichTutor
StoichTutor guides learners step by step through problems using pre-structured fields and boxes [37]. In addition to entering numeric values, units and substances must also be selected from a drop-down menu. The system provides feedback by recognizing incorrect entries and highlighting them (e.g., a box is highlighted in red). Learners can request hints, which provide specific instructions on the next problem-solving step. This type of feedback is taken into account for the evaluation, as hints are generally considered as incorrect attempts in learning rate modeling [10, 5]. For many (but not all) steps, StoichTutor provides specific guidance for incorrect inputs (e.g., also swapping numerator and denominator).1 Figure 1 visualizes StoichTutor’s interface.
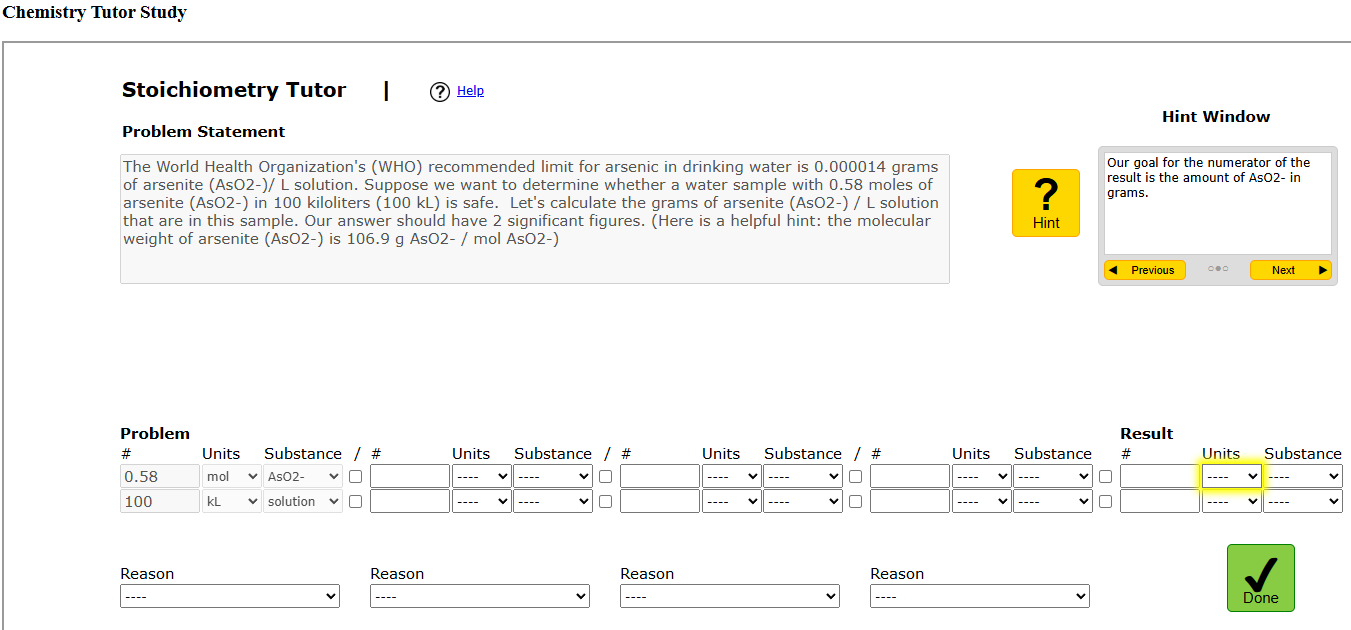
We categorized feedback in StoichTutor based on categories established by Lyster and Ranta [34] and Budiana and Mahmud [8]. As these categories originated from foreign language teaching, some adjustments were necessary to ensure a classification of the types of feedback in StoichTutor. Examples of our categories are presented in Table 1, which summarizes the types of feedback in StoichTutor. Explicit feedback and indirect feedback as well as knowledge-of-results feedback (referred to as correctness feedback) could be adopted as is. However, we combined positive and negative correctness feedback due to the low number of negative correctness feedback in StoichTutor. We included positive feedback in our model, as research on memory performance suggests that feedback affirming a correct result enhances confidence in the problem-solving process [49, 9]. We note that common cognitive models of student knowledge our field also treat incorrect and correct attempts at problem-solving steps as learning events with distinct learning rates [41].
Finally, metalinguistic feedback and elicitation [34] were listed independently. In this article, however, the definitions are summarized under the category ‘metalinguistic feedback’, as it is not possible to differentiate between them based on StoichTutor’s feedback messages. Both message types indicate an error through questions and hints, but do not offer a direct solution. In addition, a further feedback form, ‘next-step feedback’, was retained as a separate category, since hints indirectly guide learners toward direct solutions with increasing specificity [48].
| Category | Example |
|---|---|
| Explicit Correction | Since we are converting from moles, |
| we select mol in the marked box. | |
| Indirect Feedback | Keep in mind that you are converting |
| from grams to mols. | |
| metalinguistic | Use 6 in this problem, but maybe |
| Feedback | not in this term. |
| Next-Step Feedback | Determine the amount of substance |
| in moles based on one liter L. | |
| Correctness Feedback | Well done! Keep it up! |
3.2.2 Coding of Feedback Messages
Two independent coders categorized the feedback messages in StoichTutor. After the first round, the coders discussed and resolved discrepancies. It became apparent that it was difficult to differentiate between ‘elicitation’ and ‘metalinguistic feedback’ in StoichTutor feedback (see Section 3.2.1). Hence, in a second round, the coded feedback that had been assigned to the categories metalinguistic feedback and elicitation was explicitly coded again into the new categories next-step feedback and metalinguistic feedback. After two coding rounds, a category was agreed upon for each feedback message. A total of 1,169 feedback messages were double-coded, representing all unique feedback messages in StoichTutor. The final coding scheme is provided in a digital appendix.2
3.3 Instructional Factors Analysis Modeling
To estimate student learning rates, we employed IFA, an extension of the Additive Factors Model (AFM), a growth model implemented through mixed-effects logistic regression [30, 33, 12]. The dependent variable in our model was the correctness of the first attempt at a given step, coded as a binary outcome (1 = correct, 0 = incorrect). The AFM model assumes that learning occurs progressively as students accumulate practice opportunities. In the base AFM model, correctness probability is modeled as a function of learning opportunities (opp.):
where \(\tau _{\text {stud.}}\) represents individual student proficiency, \(\beta _{\text {skill}}\) denotes the initial difficulty of the skill being practiced, and \(\beta _{\text {opp.}}\) captures the learning rate per opportunity.
IFA extends this model by decomposing opportunities based on instructional factors, in this case, feedback type:
where each \(\beta _{feedback}\) term represents the learning rate of a given feedback type. Opportunities were counted separately by feedback type, following past research using IFA [12, 16].
The models were estimated using mixed-effects logistic
regression with the glmer function in R [2]. A baseline
AFM model with a single opportunity count was compared
against the IFA model with separate opportunity counts
for each feedback type using the Bayesian Information
Criterion (BIC) to compare model fit and parsimony [32].
Interpretation of the estimated learning rates by feedback type
is based on the odds ratio (\(OR\)) for each feedback type. An \(OR\)
greater than one indicates that each additional learning
opportunity associated with that feedback type increases
the probability of a correct response, suggesting effective
learning [5]. Conversely, an \(OR\) below one implies that repeated
exposure to that feedback type is associated with reduced
performance gains, which may indicate counterproductive
feedback. In addition, separate models were estimated on
data subsets for high and low prior knowledge students to
explore whether the effectiveness of feedback varied by prior
knowledge.
4. RESULTS
The double coding of feedback over two rounds resulted in a high reliability with binary kappas at category level between 0.94 (explicit correction) and 1.00 (correctness feedback). Further, model fit and parsimony of the IFA model were substantially better than the baseline AFM model which does not distinguish learning rate by feedback type, as suggested by a lower \(BIC\) (8232.9 for AFM and 7292.2 for IFA).
4.1 Feedback-Specific Learning Rate (RQ1)
Overall, StoichTutor had a good and significant (\(p<0.001\)) learning rate in this population as log of likelihood of solving problems with less number of problem-solving steps [25] required with an \(OR\) of 1.07 at a 95% \(CI\) of 1.05-1.09, indicating model validity. In log-odds representation, this learning rate corresponded to an effect size of \(\beta = 0.07\), which is slightly lower than the log-odds of 0.1 typical for tutoring systems [27]. As shown next, this difference could be due to some forms of feedback in StoichTutor being ineffective for learning. Specifically, considering the effects of different types of feedback on the learning rate (RQ1), the results of the IFA model are presented in Table 2.
| Predictors | Odds Ratios | 95% \(CI\) | p |
|---|---|---|---|
| Intercept | 1.21 | 0.88 – 1.65 | .237 |
| Explicit Correction | 1.01 | 0.72 – 1.41 | .961 |
| Correctness Feedback | 1.12 | 1.08 – 1.17 | \(<\).001 |
| Indirect Feedback | 0.73 | 0.54 – 1.00 | .048 |
| Next-Step Feedback | 0.88 | 0.81 – 0.95 | .001 |
| Metalinguistic Feedback | 0.96 | 0.89 – 1.03 | .261 |
Correctness feedback (\(OR = 1.12\), \(p < .001\)) significantly improved student learning rates, indicating that simple binary accuracy feedback (correct vs. incorrect) effectively supports skill acquisition. Conversely, indirect feedback (\(OR = 0.73\), \(p = .048\)) and next-step feedback prompts (\(OR = 0.88\), \(p = .001\)) were significantly associated with lower learning rates, suggesting that these types of feedback slowed down learning. Explicit correction (\(OR = 1.01\), \(p = .961\)) and metalinguistic Feedback (\(OR = 0.96\), \(p = .261\)) did not lead to any significant change in performance over time.
4.2 Comparison by Prior Knowledge (RQ2)
To examine if feedback effectiveness varied by prior knowledge, we analyzed high and low prior knowledge students separately (RQ2). Correctness feedback exhibited a positive learning rate in both prior knowledge groups (high: \(OR = 1.12\), \(p = .003\); low: \(OR = 1.14\), \(p < .001\)). Indirect feedback negatively impacted learning in both groups, but was not significant for either group, potentially due to lower statistical power per group. Next-step feedback had a small but significant negative effect in both groups (high: \(OR = 0.89\), \(p = .020\); low: \(OR = 0.87\), \(p = .025\)). Explicit correction and metalinguistic feedback were non-significant.
Overall, these results suggest that, contrary to expectations, learning rates by feedback type did not significantly differ by prior knowledge group. This regularity in learning rates aligns with prior large-scale evidence of learning rates in tutoring systems [27]. Specifically, correctness feedback was most consistently effective across different levels of prior knowledge, while indirect and next-step feedback may require further refinement to increase their instructional effectiveness.
5. DISCUSSION
In this study, feedback messages from a tutoring system were classified in line with past feedback taxonomies[8, 34] to investigate the extent to which student learning rates differ by feedback type (RQ1). We also analyzed learning rates associated with each feedback type across students with low and high prior knowledge (RQ2), as past research has predicted high prior knowledge students may benefit from more elaborated feedback [18, 45, 47]. To the best of our knowledge, this study is the first to apply IFA [12] to different feedback types.
Results suggest that the positive learning rate students experienced in StoichTutor was primarily due to simple correctness feedback, indicating if a given attempt was correct or not. This was the case for learners with high and low prior knowledge equally. In our study, correctness feedback was most commonly following correct problem-solving step responses, as StoichTutor only includes three cases where negative correctness feedback is used. In contrast to this (mostly positive) correctness feedback, other feedback types in our sample, more commonly following incorrect responses, were not associated with significant learning, or even slowed students down. These results align with findings from Mitrovic et al. [38], which showed that giving positive correctness feedback in addition to negative correctness feedback especially improves learning. We interpret the lack of evidence for the effectiveness of other feedback types as negative feedback impacting autonomy and the sense of competence of students [50], which in turn affects intrinsic motivation as delineated by Deci and Ryan [15]. It is possible that these motivational effects made students less likely to productively engage with the more complex forms of feedback in StoichTutor, for example, by self-explaining after an explicit correction [17, 50]. Future research could study this interpretation further through think-aloud protocols [6]. As an alternative explanation, it is possible that the feedback types in our sample are confounded with substantial differences in student performance at specific skills, which could be adjusted for by adding success history parameters into the IFA model [42]. It is possible, though beyond the scope of this study, that such confounds lead to our model underestimating the learning rate of feedback types co-occurring with errors (e.g., explicit corrections).
The fact that learning rates were similar for learners of high and low prior knowledge misaligns with past research on feedback that found that feedback on the correct answer was less effective for lower performing students when solving vector math problems [21]. Similar diversity of feedback effectiveness by context has been noted in past research [35], and it is possible that our context of stoichiometry learners in higher education are no exception.
Our results also align with past evidence that learning rates are generally similar across learners, irrespective of prior knowledge [27]. We suspect that correctness feedback gives learners more room to engage in active learning and generate answers with the help of hints, which has been shown to support learning [31]. It is possible that the more elaborated types of feedback studied here, which sometimes slowed down learners, represent overscaffolding, whereby learning is harmed if too much information about a step is provided [26]. Indeed, past research on StoichTutor suggests that its high degree of scaffolding may take away opportunities from students to effectively self-regulate their learning and generate problem-solving solution plans [51], which may diminish their learning. In contrast, hints allow learners to pace their own learning, and increasingly reveal relevant information at the learner’s request. In line with this explanation, past literature suggested that high prior knowledge may initially need to explore a learning environment independently of feedback, and that elaborated feedback is therefore not always effective [18, 45]. To further test these hypotheses, future research could employ think-aloud protocols which have been successfully used to understand strategic and metacognitive differences in chemistry problem solving [6, 4].
5.1 Limitations and Further Work
First, we acknowledge a neglect of the language style used in StoichTutor. A polite language style, in contrast to a direct language style, benefits students with low prior knowledge especially [37]. Second, we neglected metacognitive factors, such as gaming the system, which are known to interfere with the effectiveness of feedback [14, 40]. Future work could adjust for gaming as an instructional factor and quantify student effort by decomposing response times [19]. Moreover, it is possible, though beyond the scope of the present study, that learning rates differences associated with distinct feedback types depend on specific knowledge components and their difficulty [28], including in relationship to student prior knowledge, which may work together to moderate student motivation to productively engage with more complex forms of feedback [50].
6. CONCLUSION
Applying instructional factors analysis to estimate learning associated with fine-grained instructional events, we contribute novel evidence regarding the effectiveness of different feedback types in tutoring systems. Our results show that all feedback types analyzed (i.e., explicit correction, correctness feedback, indirect, next-step, and metalinguistic feedback) had comparable impacts on the learning rates of students with low and high prior knowledge. This indifference in knowledge acquisition extends past evidence that tutoring systems lead to favorable learning conditions and regular learning rates for all learners. Notably, simple correctness feedback, indicating whether a step was right or wrong, was the only type of feedback that led to a significantly positive learning rate. Meanwhile next-step and indirect feedback lead to a negative learning rate. We suspect that these more complex forms of feedback take away opportunities for learners to effectively self-regulate their learning through hints and active generation of solutions.
7. REFERENCES
- V. Aleven, J. Sewall, O. Popescu, M. van Velsen, S. Demi, and B. Leber. Reflecting on twelve years of its authoring tools research with ctat. In R. Sottilare, A. Graesser, X. Hu, and K. Brawner, editors, Design Recommendations for Adaptive Intelligent Tutoring Systems, volume 3, pages 263–283. 2015.
- D. Bates, M. Mächler, B. Bolker, and S. Walker. Fitting linear mixed-effects models using lme4. Journal of Statistical Software, 67(1):1–48, 2015.
- J. E. Beck. Using learning decomposition to analyze student fluency development. In ITS2006 Educational Data Mining Workshop, pages 21–28, June 2006.
- C. Borchers, H. Fleischer, D. J. Yaron, B. M. McLaren, K. Scheiter, V. Aleven, and S. Schanze. Problem-solving strategies in stoichiometry across two intelligent tutoring systems: A cross-national study. Journal of Science Education and Technology, 34:384–400, 2025.
- C. Borchers, K. Yang, J. Lin, N. Rummel, K. R. Koedinger, and V. Aleven. Combining dialog acts and skill modeling: What chat interactions enhance learning rates during ai-supported peer tutoring? In B. Paaßen and C. D. Epp, editors, Proceedings of the 17th International Conference on Educational Data Mining, pages 117–130, Atlanta, Georgia, USA, July 2024. International Educational Data Mining Society.
- C. Borchers, J. Zhang, R. S. Baker, and V. Aleven. Using think-aloud data to understand relations between self-regulation cycle characteristics and student performance in intelligent tutoring systems. In Proceedings of the 14th Learning Analytics and Knowledge Conference, pages 529–539, 2024.
- S. BouJaoude and H. Barakat. Students’ problem solving strategies in stoichiometry and their relationships to conceptual understanding and learning approaches. The Electronic Journal for Research in Science & Mathematics Education, 7(1), 2003.
- H. Budiana and M. Mahmud. Indirect written corrective feedback (wcf) in teaching writing. Academic Journal Perspective Education Language And Literature, 8(1):60–71, 2020.
- A. C. Butler, J. D. Karpicke, and H. L. Roediger. Correcting a metacognitive error: Feedback increases retention of low-confidence correct responses. Journal of Experimental Psychology: Learning, Memory, and Cognition, 34(4):918–928, 2008.
- H. Cen, K. Koedinger, and B. Junker. Learning factors analysis–a general method for cognitive model evaluation and improvement. In International conference on intelligent tutoring systems, pages 164–175. Springer, 2006.
- M. Chi, K. Koedinger, G. Gordon, and P. Jordan. Instructional factors analysis: A cognitive model for multiple instructional interventions. In Proceedings of the 4th International Conference on Educational Data Mining (EDM), pages 61–70, 2011.
- M. Chi, K. VanLehn, D. Litman, and P. Jordan. Empirically evaluating the application of reinforcement learning to the induction of effective and adaptive pedagogical strategies. In Proceedings of the 14th International Conference on Artificial Intelligence in Education, pages 309–316, 2011.
- A. T. Corbett and J. R. Anderson. Locus of feedback control in computer-based tutoring: impact on learning rate, achievement and attitudes. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, CHI ’01, page 245–252, New York, NY, USA, 2001. Association for Computing Machinery.
- R. S. J. d. Baker, J. Walonoski, N. Heffernan, I. Roll, A. Corbett, and K. Koedinger. Why students engage in "gaming the system". Journal of Interactive Learning Research, 19:185–224, 2008.
- E. L. Deci and R. M. Ryan. Self-determination theory: A macrotheory of human motivation, development, and health. Canadian Psychology / Psychologie Canadienne, 49(3):182–185, 2008.
- N. Diana, J. Stamper, and K. Koedinger. An instructional factors analysis of an online logical fallacy tutoring system. In Artificial Intelligence in Education: 19th International Conference, AIED 2018, London, UK, June 27–30, 2018, Proceedings, Part I 19, pages 86–97. Springer International Publishing, 2018.
- C. J. Fong, E. A. Patall, A. C. Vasquez, and S. Stautberg. A meta-analysis of negative feedback on intrinsic motivation. Educational Psychology Review, 31:121–162, 2019.
- E. Fyfe and B. Rittle-Johnson. The effects of feedback during exploration depend on prior knowledge. In Proceedings of the Annual Meeting of the Cognitive Science Society, volume 34, pages 348–353, 2012.
- A. Gurung, A. Botelho, and N. Heffernan. Examining student effort on help through response time decomposition. In Proceedings of the 14th International Conference on Educational Data Mining (EDM), pages 292–301, 2021.
- J. Hattie and H. Timperley. The power of feedback. Review of Educational Research, 77(1):81–112, 2007.
- A. F. Heckler and B. D. Mikula. Factors affecting learning of vector math from computer-based practice: Feedback complexity and prior knowledge. Physical Review Physics Education Research, 12(1):010134, 2016.
- D. A. Johnson. A component analysis of the impact of evaluative and objective feedback on performance. Journal of Organizational Behavior Management, 33(2):89–103, 2013.
- J. Y. Kim and K. Y. Lim. Promoting learning in online, ill-structured problem solving: The effects of scaffolding type and metacognition level. Computers & Education, 138:116–129, 2019.
- P. E. King, P. Schrodt, and J. J. Weisel. The instructional feedback orientation scale: Conceptualizing and validating a new measure for assessing perceptions of instructional feedback. Communication Education, 58(2):235–261, 2009.
- K. Koedinger, M. Blaser, E. McLaughlin, H. Cheng, and D. Yaron. Mathematics matters or maybe not: An astonishing independence between mathematics and the rate of learning in general chemistry. JACS Au, 2025.
- K. R. Koedinger and V. Aleven. Exploring the assistance dilemma in experiments with cognitive tutors. Educational psychology review, 19:239–264, 2007.
- K. R. Koedinger, P. F. Carvalho, R. Liu, and E. A. McLaughlin. An astonishing regularity in student learning rate. Proceedings of the National Academy of Sciences, 120(13):e2221311120, 2023.
- K. R. Koedinger, A. T. Corbett, and C. Perfetti. The knowledge-learning-instruction framework: Bridging the science-practice chasm to enhance robust student learning. Cognitive Science, 36(5):757–798, 2012.
- K. R. Koedinger, R. S. J. d. Baker, K. Cunningham, A. Skogsholm, B. Leber, and J. Stamper. A data repository for the edm community: The pslc datashop. In C. Romero, S. Ventura, M. Pechenizkiy, and R. S. J. d. Baker, editors, Handbook of Educational Data Mining, pages 43–56. CRC Press, 2010.
- K. R. Koedinger, S. D’Mello, E. A. McLaughlin, Z. A. Pardos, and C. P. Rosé. Data mining and education. Wiley Interdisciplinary Reviews: Cognitive Science, 6(4):333–353, 2015.
- K. R. Koedinger, J. Kim, J. Z. Jia, E. A. McLaughlin, and N. L. Bier. Learning is not a spectator sport: Doing is better than watching for learning from a mooc. In Proceedings of the second (2015) ACM conference on learning@ scale, pages 111–120, 2015.
- J. Kuha. Aic and bic: Comparisons of assumptions and performance. Sociological methods & research, 33(2):188–229, 2004.
- R. Liu and K. R. Koedinger. Towards reliable and valid measurement of individualized student parameters. In Proceedings of the 10th International Conference on Educational Data Mining (EDM), pages 135–142, 2017.
- R. Lyster and L. Ranta. Corrective feedback and learner uptake: Negotiation of form in communicative classrooms. Studies in Second Language Acquisition, 19(1):37–66, 1997.
- U. Maier and C. Klotz. Personalized feedback in digital learning environments: Classification framework and literature review. Computers and Education: Artificial Intelligence, 3:100080, 2022.
- F. Marais and S. Combrinck. An approach to dealing with the difficulties undergraduate chemistry students experience with stoichiometry. South African Journal of Chemistry, 62:88–96, 2009.
- B. M. McLaren, K. E. DeLeeuw, and R. E. Mayer. A politeness effect in learning with web-based intelligent tutors. International Journal of Human-Computer Studies, 69(1-2):70–79, 2011.
- A. Mitrovic, S. Ohlsson, and D. K. Barrow. The effect of positive feedback in a constraint-based intelligent tutoring system. Computers & Education, 60(1):264–272, 2013.
- M. Niaz and L. A. Montes. Understanding stoichiometry: Towards a history and philosophy of chemistry. Educación Química, 23:290–297, 2012.
- L. Paquette, A. de Carvalho, R. Baker, and J. Ocumpaugh. Reengineering the feature distillation process: A case study in detection of gaming the system. In Proceedings of the 7th International Conference on Educational Data Mining, pages 284–287. International Educational Data Mining Society, July 2014.
- P. I. Pavlik, H. Cen, and K. R. Koedinger. Performance factors analysis – a new alternative to knowledge tracing. In Artificial Intelligence in Education, pages 531–538. IOS Press, 2009.
- N. Rachatasumrit, P. Carvalho, and K. Koedinger. Beyond accuracy: Embracing meaningful parameters in educational data mining. In Proceedings of the 17th International Conference on Educational Data Mining, pages 203–210, 2024.
- R. R. Schmeck and E. L. Schmeck. A comparative analysis of the effectiveness of feedback following errors and feedback following correct responses. Journal of General Psychology, 87(2):219–223, 1972.
- V. J. Shute. Focus on formative feedback. Review of Educational Research, 78(1):153–189, 2008.
- J. Sweller, J. J. G. Van Merrienboer, and F. G. Paas. Cognitive architecture and instructional design. Educational Psychology Review, 10:251–296, 1998.
- O. Sychev, N. Penskoy, A. Anikin, M. Denisov, and A. Prokudin. Improving comprehension: intelligent tutoring system explaining the domain rules when students break them. Education Sciences, 11(11):719, 2021.
- M. Taub and R. Azevedo. How does prior knowledge influence eye fixations and sequences of cognitive and metacognitive SRL processes during learning with an intelligent tutoring system? International Journal of Artificial Intelligence in Education, 29(1):1–28, 2018.
- K. Vanlehn. The behavior of tutoring systems. International Journal of Artificial Intelligence in Education, 16:227–265, 2006.
- L. Wang and J. Yang. Effect of feedback type on enhancing subsequent memory: Interaction with initial correctness and confidence level. PsyCh Journal, 10(5):751–766, 2021.
- B. Wisniewski, K. Zierer, and J. Hattie. The power of feedback revisited: A meta-analysis of educational feedback research. Frontiers in Psychology, 10:487662, 2020.
- J. Zhang, C. Borchers, and A. Barany. Studying the interplay of self-regulated learning cycles and scaffolding through ordered network analysis across three tutoring systems. In International Conference on Quantitative Ethnography, pages 231–246. Springer, 2024.
1 The StoichTutor website is available via the following link: https://stoichtutor.cs.cmu.edu
© 2025 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.