ABSTRACT

In second language acquisition, incidental vocabulary learning refers to the process by which one’s vocabulary increases through activities in which increasing vocabulary is not the main goal. A typical example is extensive reading, where learners naturally expand their vocabulary by reading many texts and guessing the meanings of unfamiliar words. Selecting texts suitable for incidental learning requires a personalized and fine-grained estimation of each language learner’s vocabulary. If a learner does not know sufficient words in a text, then the learner cannot read through the text to guess the meanings of unfamiliar terms, so incidental learning does not occur. In contrast, if a learner knows all the words in a text, then incidental learning cannot occur because the learner has no new words to learn. Therefore, if a learner attempts to select a text that can significantly increase their vocabulary, the risk of reading failure increases along with the possibility that no words can be guessed and learned. Therefore, learners should be presented with both the amount of vocabulary they can add and risk of failure in reading, and be allowed to select the text they wish to read. To this end, we require an algorithm that can simultaneously calculate the amount of vocabulary that can be learned and relevant risk when a text is read. This paper presents an algorithm for this purpose with preliminary experimental results. Specifically, we use findings from applied linguistics that indicate that the condition for incidental learning to occur is that the percentage of words that a learner knows in a text is above a certain threshold. By modeling the estimated size of the increase in vocabulary as a random variable, our method uses the variance of the estimated size as a measure of the risk of reading failure. This allows a learner to select the text with the lowest risk among texts that have the same estimated size of increase in vocabulary. Experimental results demonstrate that our method can significantly aid learners in selecting “efficient” texts to read by identifying a handful of such texts among a library of 500 texts. The results also demonstrate that some texts are stable and efficient for many learners.

Keywords

1. INTRODUCTION

In second language acquisition, the “incidental learning” of second language vocabulary is the incidental acquisition of vocabulary through activities in which vocabulary acquisition is not the main objective. It is a concept that is widely used in applied linguistics studies [20, 28, 11]. An example of such an activity is extensive reading, where readers learn vocabulary by guessing the meanings of unfamiliar words when reading various texts. In contrast to incidental learning, learning vocabulary in the context of an activity whose main goal is vocabulary acquisition is called “intentional learning” [28, 11]. An example is acquiring second language vocabulary by memorizing lists of words. Although incidental learning is less efficient than intentional learning at increasing learner vocabulary in a second language, it is believed to have many merits. It promotes a deeper understanding of how words are used in different contexts and leads to improved learner writing skills [21].

Being able to select texts of interest to each learner also improves motivation for language learning. These merits are summarized in [21] and a combination of intentional and incidental learning is desirable [21].

Incidental learning has many advantages and is used in various scenarios. In most scenarios, for successful incidental learning, it is important to select and use texts that suit the learner [21] and various technologies that support incidental learning have been studied [9, 10, 12]. New vocabulary acquisition does not occur if a text consists only of words that have already been learned. In contrast, if a learner cannot understand sufficient words in a text, then there is a high risk of failure in reading the text, making incidental learning difficult because the learner cannot guess the meanings of words appearing in the text. In this case, even if we allow learners to use dictionaries, they are not motivated to continue learning if there are too many words that they need to look up [27, 18]. In applied linguistics, it has been reported that if a learner knows 95% to 98% of the words (tokens) in a text, then they can learn new vocabulary through incidental learning by guessing the meanings of unfamiliar words based on their context [13]. In other words, this finding from applied linguistics suggests that unlearned words in a text can be efficiently learned incidentally if a learner knows 95% to 98% of the text’s tokens [21].

This result from applied linguistics implies that text selection for efficient incidental learning should consider the risk of failure when reading the selected text. Selecting a text with a small ratio of known words (i.e., a large ratio of unknown words) may increase the size of the vocabulary acquired through incidental learning, but if the ratio of known words is below a certain threshold, then learners will not be able to continue reading the text and guess the meanings of unfamiliar words. Therefore, incidental learning will not occur and the size of vocabulary acquired will not increase. Therefore, it is desirable to select texts that appear to have the largest number of unknown words while keeping the risk of learner reading failure within an acceptable range.

In this study, we mathematically formulated a strategy for increasing vocabulary through incidental learning using machine learning. Specifically, we propose a method for determining the probability distribution of the estimated size of the vocabulary acquired through incidental learning when a learner reads a text. We modelled the variance of the estimated size as a measure of the risk of reading failure. By using our method, among many texts, learners can select a text for incidental learning by considering both the number of words to be learned (i.e., estimated size of the increase in vocabulary) and risk of failure in reading the text.

2. RELATED WORK

In educational data mining and intelligent tutoring system studies, technologies for supporting incidental learning have been studied in lifelogs [9] and dictionaries [10, 12]. However, previous studies have not focused on methods that can consider both the estimated size of the increase in vocabulary and risk of reading failure. Several researchers have also proposed methods to assess second language learner vocabularies [19, 23] and tutoring systems [26]. However, to the best of our knowledge, no study has extensively addressed text selection algorithms based on the estimated increase in second language vocabulary through incidental learning.

This study focused on the task of personalized prediction of second language vocabulary [16, 4, 15, 29, 8, 14, 6, 7], which has been studied in natural language processing. In this task, each learner takes a vocabulary test that can be completed in approximately half an hour. Then, for a word not on the test, this task aims to predict whether each test taker knows the word based on their vocabulary test results. Some previous studies have used rich information other than vocabulary tests to improve accuracy, such as individual learner characteristics and word meanings [7, 4], as well as human memory lengths [25, 24].

In particular, several studies have modeled the degree of forgetting over time considering that forgetting curves are closely related to vocabulary learning [25, 24]. However, such meticulous modeling requires time-stamped records of vocabulary learning processes, which are only provided in a few datasets. We used a vocabulary test result dataset to test the applicability of our method.

3. TASK SETTING

Here, we present a motivating example for the problem considered in this study. Consider a text consisting of $4$ words [a,b,c,d]. Let the frequency of the words be $[93,3,3,1]$. Assume that the probability of knowing each word [a,b,c,d] is [0.9,0.6,0.5,0.2], respectively. In reality, these probabilities are estimated using probabilistic classifiers trained on a vocabulary test that includes none of a, b, c, or d. Therefore, we assume that we cannot directly test whether a learner knows these words.

According to findings from applied linguistics, if a learner knows more than $95\%$ of the words in a text, they can learn unfamiliar words by reading the text. This percentage is called text coverage. Here, we enumerate the cases in an example where text coverage exceeds $95\%$. In this example, “a” occurs the most frequently, but knowing “a” alone does not ensure that the text coverage exceeds $95\%$. However, if the learner knows {a,b} and does not know {c,d}, then the coverage of the learner for the target text exceeds the threshold. If we focus only on the words that the learner knows and writes specifically, then the cases that exceed the threshold are {a,b}, {a,c}, {a,b,d}, {a,c,d}, and {a,b,c,d}.

Now, consider a case in which the learner knows words {a,b}. Because we assume that the learner does not know {c,d}, the probability of case {a,b} can be calculated as $0.9\times 0.6\times (1-0.5)\times (1-0.2)$. At this time, the aforementioned applied linguistics finding [20, 22] indicates that this learner can naturally acquire the unfamiliar words $\{c,d\}$ by reading the text. If we focus only on unfamiliar words, we can consider this probability as the probability that the learner can learn the words {c,d} by reading the text ($0.9\times 0.6\times (1-0.5)\times (1-0.2)$) through incidental learning. Similarly, the probability that the learner knows only {a,c} can also be considered as the probability that new words {b,d} can be acquired by reading the text through incidental learning.

Therefore, when considering all cases, the probability that the learner can incidentally learn each word [a,b,c,d] by reading the text is [0, 0.18, 0.27, 0.576]. If the learner does not know “a,” then they cannot read the text and incidental learning cannot occur. Therefore the probability for “a” is $0$. The expected number of words that can be acquired by reading this text is $1\times 0+1\times 0.18+1\times 0.27+1\times 0.576=1.026$. In the next section, we propose a method for not only obtaining the expectation of learning (i.e., mean of the distribution), but also the entire distribution.

4. PROPOSED FORMULATION

We formulated a motivating example in the previous section. Consider a vocabulary $\{v_1,\dots <!--\; FUNCTION\; APPLICATION\; -->,v_I\}$, where $I$ is the vocabulary size. Let $n_i$ be the number of occurrences of $v_i$ (i.e., frequency of $v_i$ in the text).

Assume that we focus on a specific learner among all $J$ learners. We denote the probability that the learner knows $v_i$ as $p_i$. Let the threshold value of text coverage be $\tau$. In the motivating example presented in the previous section, $\tau =0.95$. The probability of the text coverage exceeding this threshold can be expressed as follows. First, the total number of words in a text can be expressed as $N={\sum <!--\; FUNCTION\; APPLICATION\; -->}_{i=1}^I{n}_i$. Next, consider the following random variable $Z_i$, which is equal to $1$ if the learner knows the word $v_i$ and equal to zero $0$ otherwise. $\{Z_1,\dots <!--\; FUNCTION\; APPLICATION\; -->,Z_I\}$ are assumed to be independent of each other.

Because the number of occurrences of words known to the learner in the text is ${\sum <!--\; FUNCTION\; APPLICATION\; -->}_{i=1}^I{Z}_i{n}_i$, then text coverage can be expressed as $\frac{{\sum <!--\; FUNCTION\; APPLICATION\; -->}_{i=1}^I{Z}_i{n}_i}{N}$. Therefore, the probability that the text coverage exceeds the threshold is $P({\sum <!--\; FUNCTION\; APPLICATION\; -->}_{i=1}^I{Z}_i{n}_i\ge \mathit{N\tau })$.

The probability that the learner acquires a new word $v_i$ through incidental learning by reading the text can be formulated as follows. For incidental learning to occur, the text must be readable, so text coverage must be above the threshold. Furthermore, for a word $v_i$ to be learned, the learner must not already know the word $v_i$. Therefore, this probability can be expressed as $P(Z_i=0,{\sum <!--\; FUNCTION\; APPLICATION\; -->}_{i=1}^I{Z}_i{n}_i\ge \mathit{N\tau })$, which is hereafter denoted as $q_i$.

We wished to obtain the distribution of the number of words acquired through incidental learning from a text. Therefore, we define $A_i$ as

Here, $\{A_1,\dots <!--\; FUNCTION\; APPLICATION\; -->,A_I\}$ are assumed to be independent of each other. The number of acquired words, which is denoted as $A$, can be expressed as $A={\sum <!--\; FUNCTION\; APPLICATION\; -->}_{i=1}^I{A}_i$. Because each $A_i$ is a random variable, $A$ is also distributional.

5. SOLVING THE PROBLEM

To obtain the probability desired $P({\sum <!--\; FUNCTION\; APPLICATION\; -->}_{i=1}^I{Z}_i{n}_i\ge \mathit{N\tau })$, or the probability that the text coverage exceeds the threshold, and to obtain the distribution of the number of acquired words $A={\sum <!--\; FUNCTION\; APPLICATION\; -->}_{i=1}^I{A}_i$, we must find the probability of a random variable consisting of a sum of independent binomial distributions with different success probabilities. If the success probabilities of the distributions are equal, then their sum is also a binomial distribution based on the reproducing property of the binomial distribution. However, in this case, because the success probabilities are different, the sum does not follow a binomial distribution. This distribution is called a Poisson binomial distribution.

Regarding the second language vocabulary, in order to calculate $P({\sum <!--\; FUNCTION\; APPLICATION\; -->}_{i=1}^I{Z}_i{n}_i\ge \mathit{N\tau })$, [5] proposed a method for obtaining this type of probability using dynamic programming. Based on space limitations, we do not present their algorithm in detail in this paper. Instead, we present only an outline of their algorithm. Because ${\sum <!--\; FUNCTION\; APPLICATION\; -->}_{i=1}^I{Z}_i{n}_i$ is an integer, the condition that $\mathit{N\tau }$ or more can be attributed to the subset-sum problem. Given a target integer, the goal of the subset-sum problem is to determine if there is a subset of $\{n_1,\dots <!--\; FUNCTION\; APPLICATION\; -->,n_I\}$ that adds up to the target integer. The subset-sum problem can be solved using dynamic programming (DP). Specifically, we can use a DP table consisting of integers that can be created using subsets of $\{n_1,\dots <!--\; FUNCTION\; APPLICATION\; -->,n_i\}$. Additionally, we must determine $P(Z_i=0,{\sum <!--\; FUNCTION\; APPLICATION\; -->}_{i=1}^I{Z}_i{n}_i\ge \mathit{N\tau })$. This is computed by applying an extension to each cell of the DP table to record the probability value of $\{Z_1,\dots <!--\; FUNCTION\; APPLICATION\; -->,Z_I\}$. In the Poisson binomial distribution, ${\sum <!--\; FUNCTION\; APPLICATION\; -->}_{i=1}^I{p}_i$ is the mean and ${\sum <!--\; FUNCTION\; APPLICATION\; -->}_{i=1}^I{p}_i(1-p_i)$ is the variance. We used this fact to obtain the mean and variance values in our experiments.

6. EXPERIMENTS

For learner vocabulary test results, [4] published a dataset based on crowdsourcing. We adopted this dataset for our experiments. According to [4], in this dataset, the vocabulary size test (VST) [1], which consists of $100$ vocabulary questions, was completed by $100$ learners who had taken the TOEIC test (https://www.ets.org/toeic) using a Japan-based crowdsourcing service called Lancers. The VST is a multiple-choice test in which the test taker selects the appropriate paraphrase of a word within an English sentence from four options. To avoid questions being solved based on grammatical clues that are irrelevant to knowledge of the word such as the difference between singular and plural words, all options are designed to be grammatically correct if they are replaced with the word in question.

Using this dataset, we trained a probabilistic classifier to classify whether each learner knows a given word and used the resulting probability values as $p_i$ in Eq. (1). Because this is a binary classification problem, a neural classifier can be used. However, because improving classification performance was not the goal of this study, simple logistic regression was used to train the classifier. For the features of the classifier, we used the frequencies from the Corpus of Contemporary American English [3] and the British National Corpus [2]. The frequencies were converted into $-\log <!--\; FUNCTION\; APPLICATION\; -->(\mathit{frequency})$ values and used as features. To make personalized predictions in which the prediction results differ from learner to learner, we simply added a $J$-dimensional one-hot vector as a feature, where $J$ is the number of learners considered in the model. For this purpose, we followed the method presented by [5].

The Brown corpus was used as the set of texts for selection. To ensure that the lengths of the texts did not affect the experimental results, for each of the $500$ texts in the Brown corpus, the first $300$ tokens of the text were used in our experiments. From these $500$ texts, our goal was to select one suitable for a learner’s incidental learning.

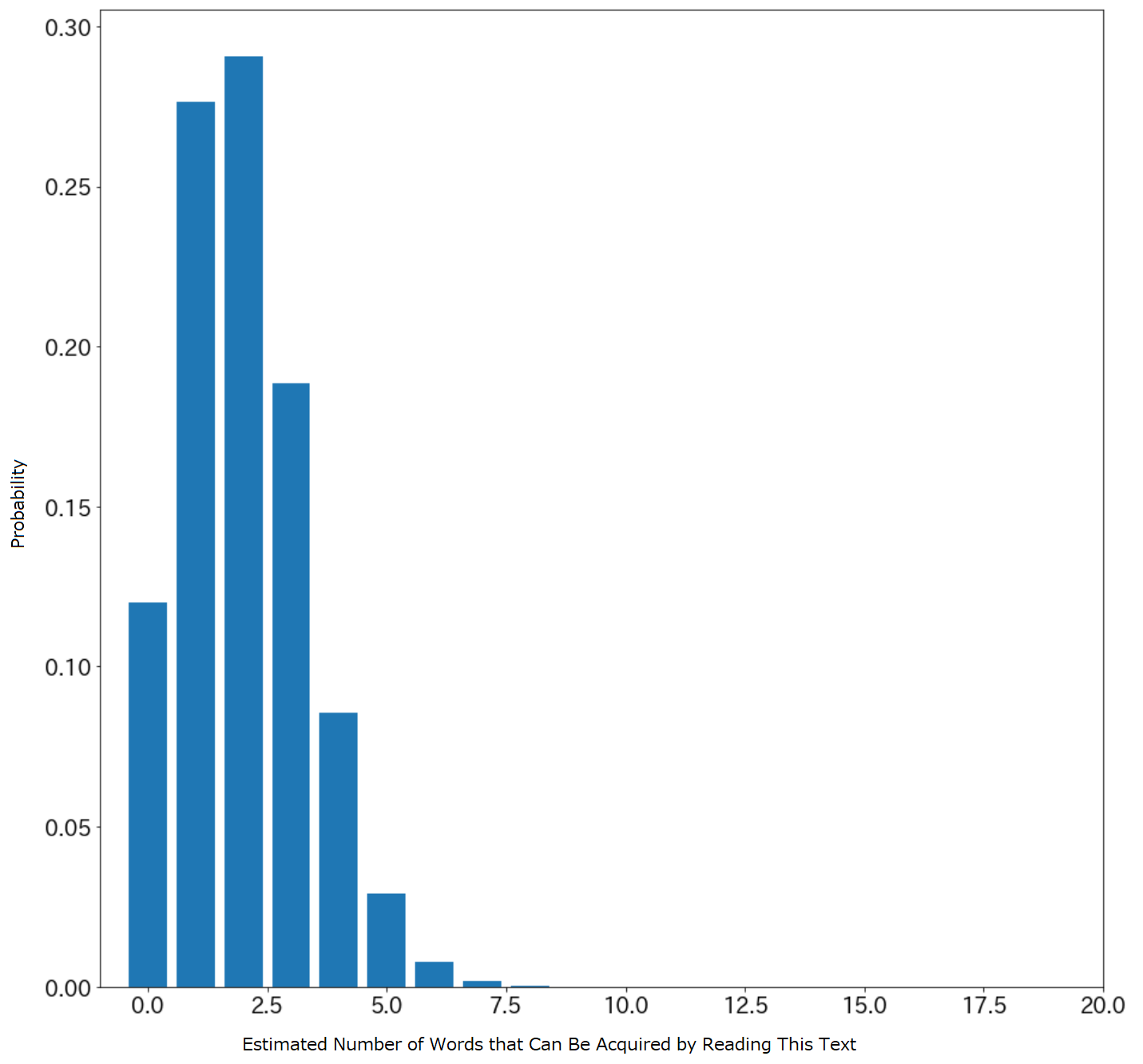
In this setting, incidental learning is likely to occur in high-performing learners because low-performing learners can read few texts from the Brown corpus. Therefore, we conducted our experiments based on the highest-performing learner, who correctly answered $96$ of the $100$ questions in the VST. We randomly selected a text from the Brown corpus and estimated the distribution of the vocabulary size acquired by this learner through incidental learning when reading the text shown in Fig. 1. This distribution is more informative compared to when only the mean is available.

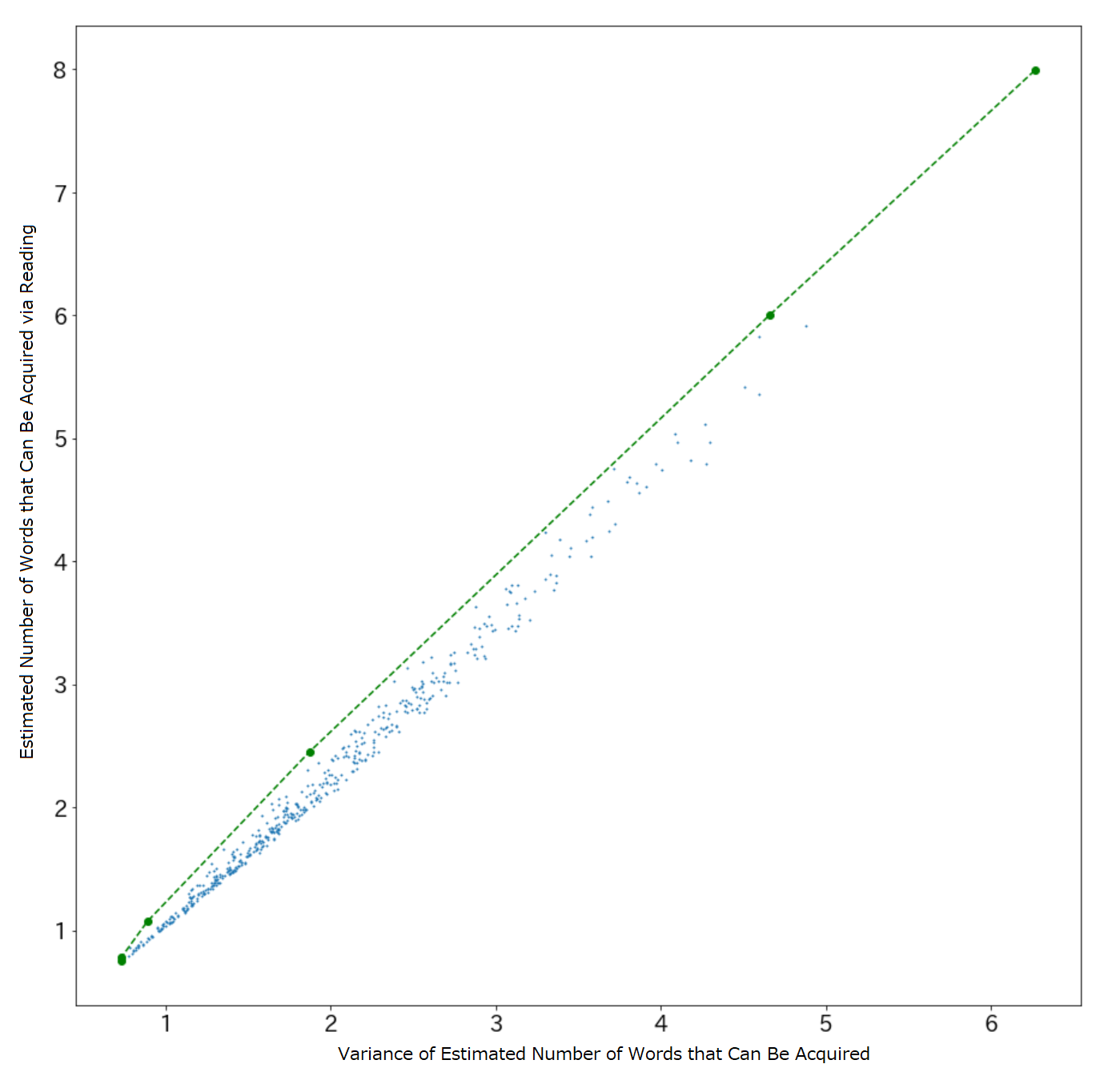
The value and variance of the expected acquired vocabulary when reading each text are considered simultaneously in Fig. 2. Each point represents a text in the Brown corpus. For a given expected size of the acquired vocabulary, it is better for the learner to select the text with the lowest possible variance in the acquired vocabulary. This allows learners to increase their vocabulary with a lower risk of reading failure. The upper-left portion of Fig. 2 presents the most efficient set of texts that promotes incidental learning for this learner. Therefore, the vertical axis in Fig. 2 can be considered as the gain and the variance of the acquired vocabulary in the horizontal axis can be considered as the risk. Fig. 2 can be considered as a risk–return plot, which is often used in finance [17].

In a risk–return plot such as in Fig. 2, selecting the upper-left points yields the lowest risk and highest gain. Therefore, the green dashed line created by connecting the upper-left points is called the efficient frontier. In Fig. 2, among the $500$ texts, $5$ texts on the efficient frontier were selected. In other words, we were able to narrow down the number of texts suitable for the learner’s incidental learning by a factor of $1∕100$. The choice of which of these $5$ texts to select depends on the degree of risk that is acceptable for learners to increase their vocabulary. Although selecting one text among $500$ is difficult for a human, selecting one text among $5$ is relatively easy.

An interesting question is whether there texts that are efficient for most learners. An experiment was conducted to answer this question. Fig. 2 presents the efficient frontier for the learner with the highest score in the vocabulary test dataset. Similarly, we identified the top $30$ highest-performing learners in a dataset consisting of $100$ learners.

Tab. A.1 presents the results. One can see that $7$ texts were selected from the efficient frontiers of more than $10$ learners, with the most common text being included in the efficient frontiers of $14$ learners. These results indicate that the texts included in the efficient frontiers of learners are relatively stable, even though efficient frontiers vary by learner.

Although we leave the quantitative analysis of the texts in Tab. A.1 for future work, the following qualitative trends can be observed. The top text (first line in Tab. A.1) exhibits clear “contrasts.” In other words, difficult words such as “contrarieties,” which many English learners presumably do not know, occur with words that they are likely to know such as “belief” and “imagination.” However, because proper nouns are treated as out-of-vocabulary words, regardless of the learner, texts with many proper nouns are also likely to be listed as efficient texts by most learners in Tab. A.1, as shown in the second row of Tab. A.1. Addressing this factor is a topic for future study.

7. CONCLUSION

To select texts suitable for vocabulary acquisition through incidental learning, we proposed a method for calculating estimates of the vocabulary acquired through incidental learning for each pair of learners and texts based on the findings of applied linguistics. By considering the size of the vocabulary acquired as a type of gain for a learner, we introduced the concept of the efficient frontiers used in financial engineering for vocabulary learning. We experimentally showed that there are “efficient” texts suitable for incidental learning that are included in the efficient frontiers of many learners.

The introduction of the concept of efficient frontiers to language learning will enable vast future work in this field, including evaluation experiments over time using learning application logs, handling the aforementioned proper noun issue, and multi-text selection when reading multiple texts simultaneously. Our approach can also be used with modern portfolio theory [17] to identify the most efficient texts.

8. ACKNOWLEDGMENTS

This work was supported by JST ACT-X Grant Number JPMJAX2006 in Japan. We used the AIST ABCI infrastructure and RIKEN miniRaiden system for computational resources. We appreciate the valuable comments from anonymous reviewers.

9. REFERENCES

1. D. Beglar and P. Nation. A vocabulary size test. The Language Teacher, 31(7):9–13, 2007.
2. T. BNC Consortium. The British National Corpus, version 3 (BNC XML Edition). 2007.
3. M. Davies. The 385+ million word corpus of contemporary american english (1990–2008+): Design, architecture, and linguistic insights. Intl. j. of corp. ling., 14(2):159–190, 2009.
4. Y. Ehara. Building an English Vocabulary Knowledge Dataset of Japanese English-as-a-Second-Language Learners Using Crowdsourcing. In Proc. of LREC, May 2018.
5. Y. Ehara. Uncertainty-Aware Personalized Readability Assessments for Second Language Learners. In 2019 18th IEEE International Conference On Machine Learning And Applications (ICMLA), pages 1909–1916, Dec. 2019.
6. Y. Ehara, Y. Baba, M. Utiyama, and E. Sumita. Assessing Translation Ability through Vocabulary Ability Assessment. In Proc. of IJCAI, 2016.
7. Y. Ehara, Y. Miyao, H. Oiwa, I. Sato, and H. Nakagawa. Formalizing Word Sampling for Vocabulary Prediction as Graph-based Active Learning. In Proc. of EMNLP, pages 1374–1384, 2014.
8. Y. Ehara, I. Sato, H. Oiwa, and H. Nakagawa. Mining Words in the Minds of Second Language Learners for Learner-specific Word Difficulty. Journal of Information Processing, 26:267–275, 2018.
9. M. N. Hasnine, K. Mouri, G. Akcapinar, M. M. H. Ahmed, and H. Ueda. A new technology design for personalized incidental vocabulary learning using lifelog image analysis. In Proceedings of the 28th international conference on computers in education (ICCE2020), pages 516–521, 2020.
10. M. Hill and B. Laufer. Type of task, time-on-task and electronic dictionaries in incidental vocabulary acquisition. 2003.
11. J. H. Hulstijn. Intentional and incidental second-language vocabulary learning: A reappraisal of elaboration, rehearsal and automaticity. 2001.
12. B. Laufer and J. Hulstijn. Incidental vocabulary acquisition in a second language: the construct of task-induced involvement. Applied Linguistics, 22(1):1–26, Mar. 2001.
13. B. Laufer and G. C. Ravenhorst-Kalovski. Lexical Threshold Revisited: Lexical Text Coverage, Learners’ Vocabulary Size and Reading Comprehension. Reading in a Foreign Language, 22(1):15–30, Apr. 2010.
14. J. Lee and C. Y. Yeung. Automatic prediction of vocabulary knowledge for learners of Chinese as a foreign language. In 2018 2nd International Conference on Natural Language and Speech Processing (ICNLSP), pages 1–4, Apr. 2018.
15. J. Lee and C. Y. Yeung. Personalizing Lexical Simplification. In Proceedings of the 27th International Conference on Computational Linguistics, pages 224–232, Santa Fe, New Mexico, USA, Aug. 2018. Association for Computational Linguistics.
16. J. Lee and C. Y. Yeung. Personalized Substitution Ranking for Lexical Simplification. In Proceedings of the 12th International Conference on Natural Language Generation, pages 258–267, Tokyo, Japan, Oct. 2019. Association for Computational Linguistics.
17. H. M. Markowitz. Foundations of portfolio theory. The journal of finance, 46(2):469–477, 1991. Publisher: JSTOR.
18. A. Mikami. Students’ attitudes toward extensive reading in the japanese efl context. Tesol Journal, 8(2):471–488, 2017.
19. B. Naismith, N.-R. Han, A. Juffs, B. Hill, and D. Zheng. Accurate Measurement of Lexical Sophistication in ESL with Reference to Learner Data. In Proceedings of the 11th International Conference on Educational Data Mining, pages 259–265, Buffalo, NY, USA, 2018. International Educational Data Mining Society (IEDMS).
20. T. Nakata and I. Elgort. Effects of spacing on contextual vocabulary learning: Spacing facilitates the acquisition of explicit, but not tacit, vocabulary knowledge. Second Language Research, 37(2):233–260, 2021. _eprint: https://doi.org/10.1177/0267658320927764.
21. I. Nation and R. Waring. Teaching extensive reading in another language. Routledge, 2019.
22. P. Nation. How much input do you need to learn the most frequent 9,000 words? 2014. Publisher: University of Hawaii National Foreign Language Resource Center.
23. R. Paiva, I. I. Bittencourt, W. Lemos, A. Vinicius, and D. Dermeval. Visualizing Learning Analytics and Educational Data Mining Outputs. In C. Penstein Rosé, R. Martínez-Maldonado, H. U. Hoppe, R. Luckin, M. Mavrikis, K. Porayska-Pomsta, B. McLaren, and B. du Boulay, editors, Artificial Intelligence in Education, pages 251–256, Cham, 2018. Springer International Publishing.
24. S. Reddy, S. Levine, and A. Dragan. Accelerating human learning with deep reinforcement learning. In NIPS workshop: teaching machines, robots, and humans, 2017.
25. B. Settles and B. Meeder. A Trainable Spaced Repetition Model for Language Learning. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 1848–1858, Berlin, Germany, Aug. 2016. Association for Computational Linguistics.
26. A. Sinclair, K. McCurdy, C. G. Lucas, A. Lopez, and D. Gaševic. Tutorbot Corpus: Evidence of Human-Agent Verbal Alignment in Second Language Learner Dialogues. International Educational Data Mining Society, July 2019. Publication Title: International Educational Data Mining Society.
27. N. Suk. The effects of extensive reading on reading comprehension, reading rate, and vocabulary acquisition. Reading Research Quarterly, 52(1):73–89, 2017.
28. G. Yali. L2 Vocabulary Acquisition Through Reading —Incidental Learning and Intentional Learning. Chinese Journal of Applied Linguistics, 33:pp. 74–93, 2010.
29. C. Y. Yeung and J. Lee. Personalized Text Retrieval for Learners of Chinese as a Foreign Language. In Proc. of COLING, pages 3448–3455, Aug. 2018.

APPENDIX

A. EXAMPLES OF EFFICIENT TEXTS

Tab. A.1 lists the texts that are frequently on the efficient frontiers of the top 30 learners.

B. DATASET AND CODE

The dataset used in this study was published in [4]. We plan to release our code at http://yoehara.com/ or
http://readability.jp/.

C. DISCUSSION

The fact that the top 30 is chosen in Tab. A.1 does not mean that, in general, our method cannot support less skilled learners. In this case, our experiments assume a situation where the test-takers in the [4] dataset were to conduct extensive reading on the texts taken from the Brown Corpus. What matters is this combination: the Brown Corpus is simply too difficult for less skilled learners on [4], and incidental learning does not occur. If we use a text set easier than Brown Corpus, incidental learning is more likely to occur even for low-ability learners, and the proposed method may be effective.

© 2022 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.