ABSTRACT
We propose in this work a novel approach to retrieve the prerequisite structure of a domain model from learner traces. We introduce the E-PRISM framework that includes the causal effect of prerequisite relationships in the learner model for predicting the learner’s performance with knowledge tracing. By studying the distribution of the learned values of each learner model parameter from synthetic data, we propose new metrics for measuring the existence, direction, and strength of a prerequisite relationship. We apply the same methodology to real-world datasets and observe promising results in retrieving the prerequisite structure of a domain model from learner traces.
Keywords
Bayesian networks, knowledge tracing
1. INTRODUCTION
The prerequisite relationships, which describe dependencies between knowledge components, play a crucial role in determining the most effective instruction sequence for students. The objective of this research is to answer the following question: is it possible to propose a learner model where the parameters are enough interpretable to detect the domain model’s prerequisite relationships, on top of predicting the learner performance?
We introduce the E-PRISM framework, which relies on an interpretable learner model, to analyze learners’ data and detect the prerequisite structure of the domain model. We summarize our contributions in this work as follows. First, we introduce an effective and tractable method for incorporating prerequisite relationships into a continuous scale of the learning process. Second, we define new metrics for assessing the causal impact of prerequisite relationships utilizing the interpretable parameters of the E-PRISM learner model and we apply them to real-world datasets.
2. DISCOVERING THE PREREQUISITESTRUCTURE OF THE DOMAIN MODEL THROUGH LEARNER MODELING
We provide an overview of the current state-of-the-art methods for retrieving the prerequisite structure of the domain model through learner modeling. We focus specifically on the learner performance prediction models and how they are used in the literature to determine the prerequisite structure within a domain model.
2.1 Approaches in learner modeling
In the field of learner modeling a variety of algorithms can be used to predict students’ performance on assessments, diagnose their strengths and weaknesses, and track their learning progress over time.
One of the popular and used methods is logistic regression, a statistical model to predict the likelihood of an event occurring given a set of predictors or independent variables. Some logistic regression algorithms, such as IRT [11] and MIRT [19], use simple features, while others, such as LFA [2], PFA [17], DAS3H [3], and Best-LR [9], use engineered and more complex features.
Besides, cognitive diagnosis algorithms model the learner’s knowledge state to predict their answers. Non-temporal Bayesian network (BN) approaches, such as DINA [10], NIDA [14], and DINO [21], use BNs to compute the probability of answering correctly by modeling the learner’s mastery of Knowledge Components (KCs). Bayesian Knowledge Tracing (BKT) uses BNs to track the learner’s knowledge over time [5] and assumes knowledge states to be dynamic.
Deep learning techniques have been applied to learner modeling and have gained popularity due to their ability to learn and extract features from large and complex datasets automatically. Deep Knowledge Tracing (DKT) is a deep learning model for the knowledge tracing task using a neural network to learn a non-linear model of the learner’s knowledge, allowing it to capture more complex patterns and make more accurate predictions [18]. Variants of DKT have been developed, but they generally only show minor performance gains compared to the original DKT model [20], except Self-Attentive Knowledge Tracing (SAKT) [16]. However, Jaeger has reported that even the more interpretable deep learning techniques are less interpretable than probabilistic graphical models such as BNs [12].
2.2 Prerequisite structure in learner models
A priori knowledge of the domain to construct a model of the prerequisite structure has been integrated into simple learner models, most of the time with Bayesian networks (BN) [4, 1]. These techniques typically involve experts using their domain knowledge to define the prerequisite relationships between the KCs through the probabilities in the networks. Also, works employ data to retrieve the conditional probabilities that rule such BNs [7].
Another approach to retrieve the prerequisite structure of the domain model is to use the predicted knowledge states of a learner over time. The idea is to use the predictions made by a learner model, which estimates the learner’s knowledge state at different points in time, to infer the prerequisite relationships between the knowledge components [18, 7]. This can be done by comparing the masteries of the different knowledge components over time. The prerequisite structure of the domain model can then be determined by conducting a statistical study of these inferred states.
Finally, the work of Käser et al. is notable for its use of a Dynamic Bayesian Network (DBN) to model the effect of the prerequisite structure between knowledge components in learner models [15]. The DBN includes arcs between the variables of related KCs’ mastery, which allows for modeling the causal effect of relationships between KCs. However, as the number of prerequisite KCs increases, the DBN’s conditional probability distributions (CPDs) can become complex to interpret. The number of parameters grows exponentially with the number of prerequisite relationships and can be challenging to analyze. Despite this limitation, Käser’s approach is a promising method for modeling the prerequisite structure in learner models, as it allows for explicitly modeling the causal effect of relationships between KCs.
3. E-PRISM: EMBEDDINGPREREQUISITE RELATIONSHIPS IN STUDENT MODELING
In this research work, we introduce a new student modeling framework called E-PRISM (for Embedding Prerequisite Relationships in Student Modeling). The E-PRISM domain model supposes a decomposition of the domain knowledge into Knowledge Components (KCs). The E-PRISM learner model assumes the learner knowledge defined as the binary masteries of each KC in the domain model. Predictions about learners’ knowledge state and performance are made from data on the learner’s interactions with learning systems.
3.1 Overview of the E-PRISM learner model
The learner model in E-PRISM is a knowledge-tracing model that considers variables for the mastery of several KCs of the domain model. Knowledge tracing is performed through a dynamic Bayesian network (DBN) which models the mastery of KCs over time. The DBN leverages the causal effect of the learning process and the causal effect of the prerequisite relationships to infer learners’ knowledge states at any time.
E-PRISM has a key feature that sets it apart from other student modeling frameworks. It utilizes ICI-based conditional probability distributions (CPDs) [8] to model the causal effects of the learning process and the prerequisite relationships on the KC mastery at each timeslice. This defines KC mastery variables as deterministic functions of variables representing the independent causal effects that influence them. We represent the part of the DBN associated with the mastery of a KC \(\mathfrak {X}\) at a time \(t>0\) in Figure 1.
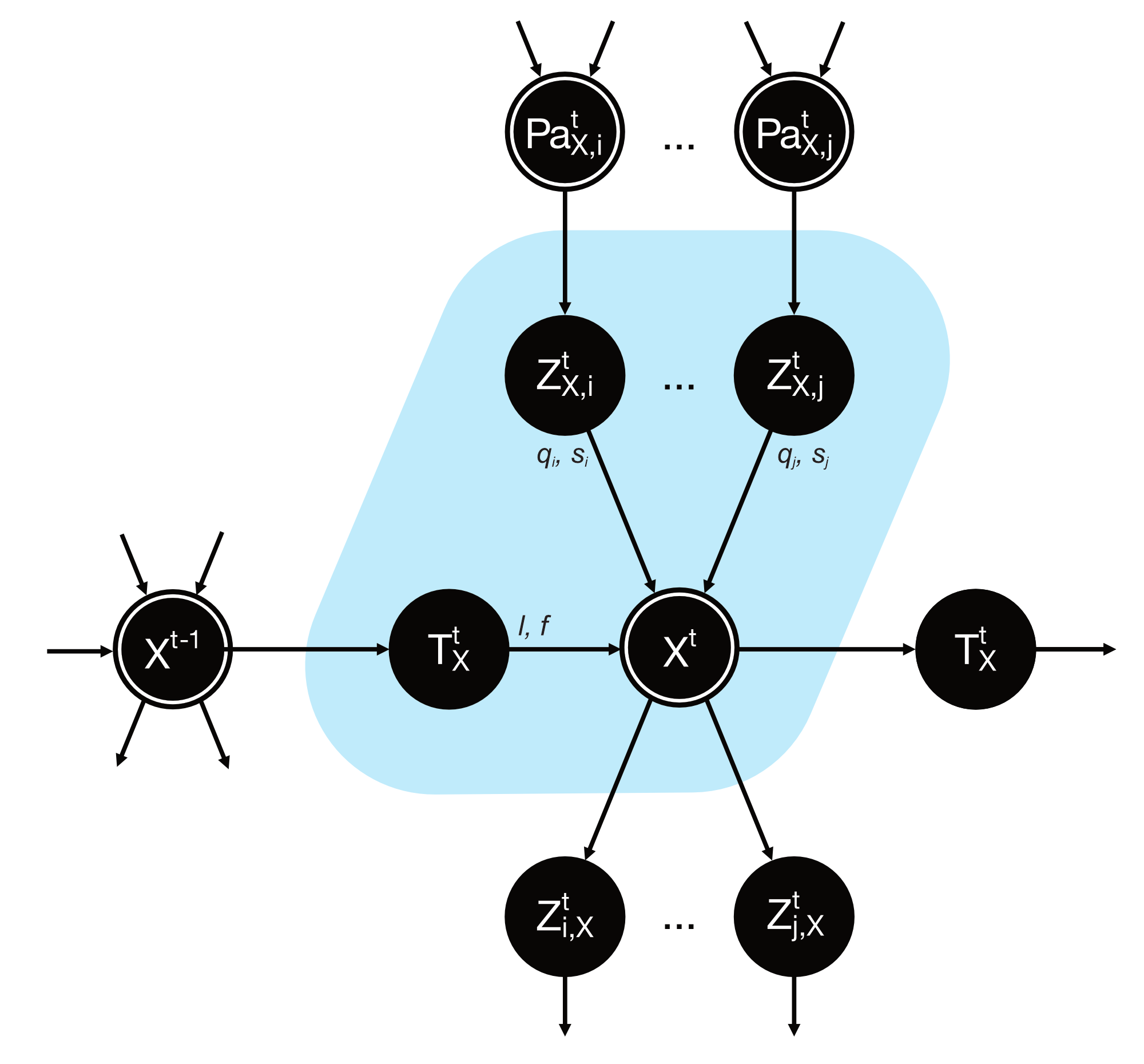
The DBN is composed of Noisy-AND gates for each KC and each timeslice. We represent a toy example of the DBN in Figure 2. The parameters of the DBN are learned with the Monte-Carlo Expectation-Maximization (MCEM) algorithm [23]. The MCEM algorithm is a variant of the Expectation-Maximization (EM) algorithm [6]. It considers the expectations of the E-step to be approximated with a Monte-Carlo sampling, which is the Blocking Gibbs sampling (BGS) [13] in our research. MCEM with BGS allows for a converging and tractable parameter learning of the learner model in E-PRISM.
3.2 Interpretability of parameters
ICI-based CPDs rely on a pair of parameters for each causal effect. In the E-PRISM learner model, there are parameters associated with the learning process, namely \((l_\mathfrak {X}, f_\mathfrak {X})\) for each KC \(\mathfrak {X}\), and parameters associated with the prerequisite relationship, namely for \((q_{\mathfrak {X}, i}, s_{\mathfrak {X}, i})\) each prerequisite \(i\) of each KC \(\mathfrak {X}\). \(l_\mathfrak {X}\) and \(f_\mathfrak {X}\) parameters are the probabilities of learning and forgetting \(\mathfrak {X}\). \(q_{\mathfrak {X}, i}\) is the probability that the \(i\)-th prerequisite of \(\mathfrak {X}\) is not sufficient to master \(\mathfrak {X}\). On the other hand, \(s_{\mathfrak {X}, i}\) is the probability the \(i\)-th prerequisite of \(\mathfrak {X}\) is not necessary to master \(\mathfrak {X}\). These interpretable parameters allow for a clear understanding of the causal effects of the learning process and prerequisite relationships on the learner’s performance. E-PRISM allows for the identification and understanding of the prerequisite structure of the domain model, which is a key focus of our research.
3.3 Metrics from E-PRISM
First, we highlight the gain of performance induced by the presence of an effective prerequisite relationship in the E-PRISM learner model. We wonder if the difference between the Root Mean Squared Error (RMSE) values obtained from different E-PRISM learner models depends on their prerequisite structure. We generate three synthetic datasets \(\mathcal {D}_\varnothing \), \(\mathcal {D}_{\text {weak}}\), and \(\mathcal {D}_\text {strong}\). \(\mathcal {D}_\varnothing \) is generated from an E-PRISM learner model considering no prerequisite relationship between \(\mathfrak {A}\) and \(\mathfrak {B}\). \(\mathcal {D}_\text {strong}\) is generated from an E-PRISM learner model that considering a strong prerequisite relationship \(\mathfrak {A}\rightarrow \mathfrak {B}\). \(\mathcal {D}_{\text {weak}}\) is generated from an E-PRISM learner model considering a weak prerequisite relationship \(\mathfrak {A}\rightarrow \mathfrak {B}\). By generating these synthetic datasets, we will be able to study the performance of the E-PRISM framework in different scenarios where the prerequisite relationship between \(\mathfrak {A}\) and \(\mathfrak {B}\) is varied. We learn the parameters of three E-PRISM learner models, namely \(e\Delta _\varnothing \), \(e\Delta _{\mathfrak {A}\rightarrow \mathfrak {B}}\), and \(e\Delta _{\mathfrak {B}\rightarrow \mathfrak {A}}\). \(e\Delta _\varnothing \) assumes no prerequisite relationship, while \(e\Delta _{\mathfrak {A}\rightarrow \mathfrak {B}}\) and \(e\Delta _{\mathfrak {B}\rightarrow \mathfrak {A}}\) respectively assume \(\mathfrak {A}\rightarrow \mathfrak {B}\) and \(\mathfrak {B}\rightarrow \mathfrak {A}\). We run 1000 simultaneous instances of the MCEM algorithm, with parameters \(N_\text {Gibbs}=10\) and \(M=0\), to perform E-PRISM parameter learning. The full synthetic dataset is used as a training dataset. We report the RMSE values obtained from parameter learning in Table 1.
| Method | RMSE on \(\mathcal {D}_{\mathfrak {A}\rightarrow \mathfrak {B}, \text {strong}}\) |
|---|---|
| \(e\Delta _\varnothing \) | 0.353 |
| \(e\Delta _{\mathfrak {A}\rightarrow \mathfrak {B}}\) | 0.327 |
| \(e\Delta _{\mathfrak {B}\rightarrow \mathfrak {A}}\) | 0.394 |
We assume the presence of an effective prerequisite relationship in the E-PRISM learner model enhances the model’s performance. Thus, to study a prerequisite relationship \(\mathfrak {A}\rightarrow \mathfrak {B}\), we can compare the performance of \(e\Delta _{\mathfrak {A}\rightarrow \mathfrak {B}}\), the E-PRISM learner model that considers the relationship \(\mathfrak {A}\rightarrow \mathfrak {B}\), and \(e\Delta _\varnothing \), the model with no prerequisite relationship. We define the \(LeP\!P\!E\!D\) (for Learner Performance Prediction Error Difference) metric to identify the existence and the direction of the prerequisite relationship. We compute the relative difference between their RMSE value obtained after learning parameters. LePPED is computed in Equation \eqref{eq:m1}. It senses the direction of the prerequisite relationship between two KCs.
\begin {equation} \label {eq:m1} LeP\!P\!E\!D(\mathfrak {A}\rightarrow \mathfrak {B}) = \frac {1}{K} \frac {(\text {RMSE of }e\Delta _\varnothing - \text {RMSE of } e\Delta _{\mathfrak {A}\rightarrow \mathfrak {B}})}{\text {RMSE of }e\Delta _\varnothing } \end {equation} where \(K\) is a normalizing constant.
\(LeP\!P\!E\!D(\mathfrak {A}\rightarrow \mathfrak {B})\) is a measure for the existence of the prerequisite relationship, as it indicates how better the E-PRISM model performs by considering \(\mathfrak {A}\rightarrow \mathfrak {B}\). \(LeP\!P\!E\!D\) ranges from \(-1\) (very unlikely there exists a relationship \(\mathfrak {A}\rightarrow \mathfrak {B}\)) to \(1\) (very likely there exists a relationship \(\mathfrak {A}\rightarrow \mathfrak {B}\)).
Upon analyzing the distributions of the E-PRISM parameter learned values, we observed shifts in the value of the parameter when the direction of an effective prerequisite relationship is reversed. We introduce a custom metric CPVD (for Comparing Peak Values of the Distribution) computed by comparing the peak values of the learned parameter distributions. CPVD is defined in Equation \eqref{eq:m2}. \begin {align} \label {eq:m2} \begin {split} CPVD(\mathfrak {A}\rightarrow \mathfrak {B}) = \frac {1}{6} &\left (\mathds {1}(l_\mathfrak {A}^{\mathfrak {A}\rightarrow \mathfrak {B}} > l_\mathfrak {A}^{\mathfrak {B}\rightarrow \mathfrak {A}})\right . + \mathds {1}(l_\mathfrak {B}^{\mathfrak {A}\rightarrow \mathfrak {B}} < l_\mathfrak {B}^{\mathfrak {B}\rightarrow \mathfrak {A}}) \\ &+ \mathds {1}(f_\mathfrak {A}^{\mathfrak {A}\rightarrow \mathfrak {B}} < f_\mathfrak {A}^{\mathfrak {B}\rightarrow \mathfrak {A}}) + \mathds {1}(f_\mathfrak {B}^{\mathfrak {A}\rightarrow \mathfrak {B}} > f_\mathfrak {B}^{\mathfrak {B}\rightarrow \mathfrak {A}})\\ &+ \left . \mathds {1}(q^{\mathfrak {A}\rightarrow \mathfrak {B}} > q^{\mathfrak {B}\rightarrow \mathfrak {A}}) + \mathds {1}(s^{\mathfrak {A}\rightarrow \mathfrak {B}} < s^{\mathfrak {B}\rightarrow \mathfrak {A}})\right ) \end {split} \end {align}
where \(\mathds {1}\) is the identity function.
CPVD is an indicator of the existence and the direction of the prerequisite relationship. It ranges from 0 to 1. The greater \(\textit {CPVD}(\mathfrak {A}\rightarrow \mathfrak {B})\), the most likely the existence of the \(\mathfrak {A}\rightarrow \mathfrak {B}\) relationship.
Finally, we benefit from the enhanced interpretability allowed by ICI-model CPDs in the E-PRISM learner model. We observe the distribution of the learned values of \(q\) and \(s\) parameters in the different situations for the E-PRISM parameter learning procedure. Specifically, we study E-PRISM learner models that either assume the correct or the wrong direction of the prerequisite relationship \(\mathfrak {A}\rightarrow \mathfrak {B}\), which is expressed in the data strongly (through \(\mathcal {D}_\text {strong}\)) or weakly (through \(\mathcal {D}_\text {strong}\)).
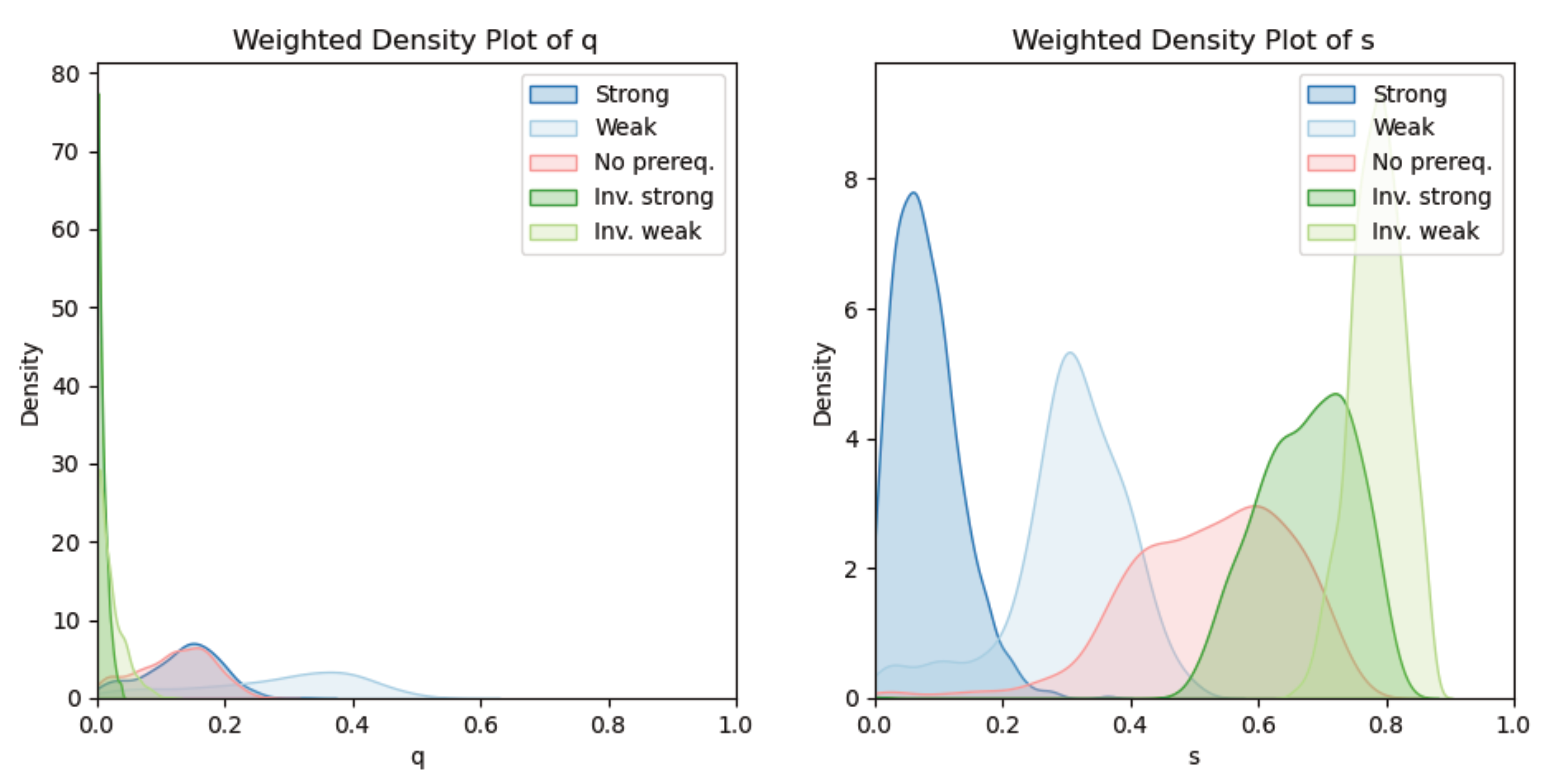
Based on these previous observations, we propose a novel metric based on the distribution of the \(s\) parameter learned values. This second metric \(\mathcal {N}\!ec\) is calculated by determining the proportion of learned values of \(s\) lower than 0.2 obtained in all the runs of parameter learning. It stands for the strength of the prerequisite relationship, according to the interpretation of the \(s\) parameter. The closer to 1 the value of \(\mathcal {N}\!ec\), the stronger the prerequisite relationship between the two considered KCs.
\begin {equation} \label {eq:m3} \mathcal {N}\!ec = \frac {1}{K}\frac {\text {Number of learned parameter values lower than 0.2}}{\text {Total number of learned parameter values}} \end {equation} with \(K\) a normalizing constant.
By combining these three metrics, we should be able to gain a deeper understanding of the interpretability of the E-PRISM learned parameters, and how they can be employed to retrieve the prerequisite structure (existence, direction, and strength) of the domain model in E-PRISM.
4. DISCOVERY OF THE PREREQUISITE STRUCTURE FROM REAL-WORLD DATA
4.1 Method
We study real-world data to evaluate the generalizability of the proposed metrics for measuring the existence, direction, and strength of prerequisite relationships.
We evaluate the capacity of our model to search for the existence, direction, and strength of prerequisite relationships in the ASSISTments12, Eedi2020, and Kartable datasets. ASSISTments12 is issued from the ASSISTment system, with a relatively coarse granularity of KCs. Eedi2020 was released as part of a NeurIPS2020 challenge and is issued from the Eedi system. Kartable is provided by Kartable and is not freely available.
We focus on the study of pairs of KCs because of tractability issues of E-PRISM with larger domain models. We consider the sub-datasets restricted to pairs of KCs and restrict each sub-dataset to learner traces from students that trained both KCs. Specifically, we have selected the 6 pairs of KCs with the highest number of learners transactions. Selected pairs of KCs are listed in Table 4 in Appendix A. Additionally, we only consider seven transactions per learner in the parameter learning procedure to ensure its tractability.
4.2 Study of the proposed metrics
| Order | Relationship | \(LeP\!P\!E\!D\) | Relationship | \(\textit {CPVD}\) | Relationship | \(\mathcal {N}\!ec\) |
|---|---|---|---|---|---|---|
| 1 | ASI \(\rightarrow \) ASF | 1 | ASPD \(\rightarrow \) MDPD | 1 | Root \(\rightarrow \) Solve | 1 |
| 2 | Chart \(\rightarrow \) Solve | 0.85 | Solve \(\rightarrow \) Chart | 1 | MMD \(\rightarrow \) MAS | 0.89 |
| 3 | ASI \(\rightarrow \) MDI | 0.72 | Root \(\rightarrow \) OR | 0.92 | Solve \(\rightarrow \) CF | 0.89 |
| 4 | Root \(\rightarrow \) OR | 0.56 | Root \(\rightarrow \) Solve | 0.92 | Solve \(\rightarrow \) Chart | 0.89 |
| 5 | Solve \(\rightarrow \) Chart | 0.54 | MDI \(\rightarrow \) ASI | 0.83 | ASF \(\rightarrow \) DF | 0.78 |
| 6 | ASF \(\rightarrow \) DF | 0.49 | ASI \(\rightarrow \) ASF | 0.83 | E \(\rightarrow \) ASI | 0.78 |
| 7 | MMD \(\rightarrow \) MAS | 0.45 | FHCF \(\rightarrow \) MLCM | 0.83 | MAS \(\rightarrow \) MMD | 0.78 |
| 8 | PNPF \(\rightarrow \) FHCF | 0.44 | PNPF \(\rightarrow \) MLCM | 0.83 | ASPD \(\rightarrow \) MDPD | 0.67 |
| 9 | VNP \(\rightarrow \) MMD | 0.42 | VNP \(\rightarrow \) MMD | 0.75 | MPDP \(\rightarrow \) ASPD | 0.67 |
| 10 | MDI \(\rightarrow \) ASI | 0.34 | ASF \(\rightarrow \) DF | 0.58 | FHCF \(\rightarrow \) MLCM | 0.67 |
| 11 | OR \(\rightarrow \) Root | 0.33 | FHCF \(\rightarrow \) PNPF | 0.58 | PNPF \(\rightarrow \) MLCM | 0.67 |
| 12 | MMD \(\rightarrow \) VNP | 0.29 | MAS \(\rightarrow \) VNP | 0.58 | Root \(\rightarrow \) OR | 0.56 |
| 13 | DF \(\rightarrow \) ASF | 0.28 | Chart \(\rightarrow \) CF | 0.58 | CF \(\rightarrow \) Chart | 0.56 |
| 14 | ASF \(\rightarrow \) MF | 0.23 | ASF \(\rightarrow \) MF | 0.5 | ASF \(\rightarrow \) MF | 0.44 |
| 15 | MAS \(\rightarrow \) MMD | 0.23 | ASI \(\rightarrow \) E | 0.42 | ASI \(\rightarrow \) ASF | 0.44 |
We wonder how the metrics relate to the prerequisite structure of the domain model with real-world data. We report metrics’ values for each selected pair of KCs in Table 2.
Some of the relationships with high custom metric scores are prerequisite relationships according to common knowledge. In particular, relationships between addition KC and multiplication KC are greatly represented. The ordering of metric values can be interpreted as a prerequisite relationship strength. Metrics CPVD and \(\mathcal {N}\!ec\) show great performance for relationships Determine if a real number is a root of a quadratic polynomial \(\rightarrow \) Give the roots of a quadratic polynomial, Give the roots of a quadratic polynomial \(\rightarrow \) Give the sign chart of a quadratic polynomial, and Addition and Subtraction Positive Decimals \(\rightarrow \) Multiplication and Division Positive Decimals. We can clearly observe that these detected prerequisite relationships, thanks to the CPVD and \(\mathcal {N}\!ec\) metrics, are coherent with the mathematics domain knowledge. Nevertheless, we remark that there is also a relationship suggesting that Multiplication and Division Integers is a requirement of Addition and Subtraction Integers. These relationships should be submitted for the approval of experts in the domain.
4.3 Relative agreement between metrics
We study the relative agreement between introduced metrics for asserting the correctness of the inferred prerequisite structure. To do so, we compute the Cohen kappa [22] between the metric predictors. For each sub-dataset, we evaluate the reliability between metrics on the existence and direction of the corresponding prerequisite relationship.
For every KCs \(\mathfrak {A}\) and \(\mathfrak {B}\), we define predictors on the existence of the prerequisite relationship \(\mathfrak {A}\rightarrow \mathfrak {B}\) from each metric by checking if they are positive. Similarly, predictors for the correct direction of the prerequisite relationship are introduced by comparing the metric value of both directions of the relationship between \(\mathfrak {A}\) and \(\mathfrak {B}\). We also introduce a predictor that combines the two conditions, and we present the results in Table 3.
| Existence | Direction | Ex. + Dir. | ||
|---|---|---|---|---|
| \(LeP\!P\!E\!D\) | CPVD | 0.133 | 0.325 | 0.111 |
| \(LeP\!P\!E\!D\) | \(\mathcal {N}\!ec\) | \(-0.071\) | 0.55 | 0.117 |
| CPVD | \(\mathcal {N}\!ec\) | 0.053 | 0.55 | 0.778 |
We observe that the predictors of the existence of the prerequisite relationship give different results depending on the employed metric. The predictors for the direction of the prerequisite relationships grossly agree with each other, especially \(LeP\!P\!E\!D\) with \(\mathcal {N}\!ec\) and CPVD with \(\mathcal {N}\!ec\). Finally, when considering the two conditions in the predictor, we observe a strong agreement between CPVD and \(\mathcal {N}\!ec\), CPVD and \(\mathcal {N}\!ec\) then suggest the same relationships to be part of the prerequisite structure of the domain. On the other hand, we observe a weak agreement (near random) between \(LeP\!P\!E\!D\) and the other metrics.
This result suggests that RMSE is not sufficient to infer the prerequisite relationships from data, even if it can be interpreted as a first filter to determine the existence of the prerequisite structure with \(LeP\!P\!E\!D\). Nevertheless, even if the relevance of CPVD and \(\mathcal {N}\!ec\) have been confirmed by the results, they should be compared with the predictions of experts, to assess that the joint agreement between CPVD and \(\mathcal {N}\!ec\) indeed corresponds to the correct prerequisite structure.
5. CONCLUSIONS AND PERSPECTIVES
In conclusion, this work presents a novel approach for leveraging the causal effect of prerequisite relationships to infer students’ knowledge state over time. The E-PRISM framework, which utilizes Dynamic Bayesian Networks (DBNs) to predict student performance, is based on a set of interpretable parameters that sense the causal effect of the learning process and the structure of prerequisite relationships in a specific domain. Our study demonstrates the ability of these parameters to compute metrics, such as CPVD and \(\mathcal {N}\!ec\), which can infer the existence, direction, and strength of prerequisite relationships. Our results, applied to the domain of mathematics, indicate the existence of common knowledge prerequisite relationships. However, further research is necessary to verify the effectiveness of these predictions by examining each inferred relationship from an expert’s point of view. In summary, this work presents a promising approach for inferring prerequisite relationships in educational data mining from analyzing an interpretable learner model.
6. REFERENCES
- C. Carmona, E. Millán, J.-L. Pérez-de-la Cruz, M. Trella, and R. Conejo. Introducing prerequisite relations in a multi-layered bayesian student model. In International conference on user modeling, pages 347–356. Springer, 2005.
- H. Cen, K. Koedinger, and B. Junker. Learning factors analysis–a general method for cognitive model evaluation and improvement. In International conference on intelligent tutoring systems, pages 164–175. Springer, 2006.
- B. Choffin, F. Popineau, Y. Bourda, and J.-J. Vie. Das3h: modeling student learning and forgetting for optimally scheduling distributed practice of skills. arXiv preprint arXiv:1905.06873, 2019.
- C. Conati, A. Gertner, and K. Vanlehn. Using bayesian networks to manage uncertainty in student modeling. User modeling and user-adapted interaction, 12(4):371–417, 2002.
- A. T. Corbett and J. R. Anderson. Knowledge tracing: Modeling the acquisition of procedural knowledge. User modeling and user-adapted interaction, 4(4):253–278, 1994.
- A. P. Dempster, N. M. Laird, and D. B. Rubin. Maximum likelihood from incomplete data via the em algorithm. Journal of the Royal Statistical Society: Series B (Methodological), 39(1):1–22, 1977.
- M. C. Desmarais, P. Meshkinfam, and M. Gagnon. Learned student models with item to item knowledge structures. User Modeling and User-Adapted Interaction, 16(5):403–434, 2006.
- F. J. Dıez and M. J. Druzdzel. Canonical probabilistic models for knowledge engineering. UNED, Madrid, Spain, Technical Report CISIAD-06-01, 2006.
- T. Gervet, K. Koedinger, J. Schneider, T. Mitchell, et al. When is deep learning the best approach to knowledge tracing? Journal of Educational Data Mining, 12(3):31–54, 2020.
- E. H. Haertel. Using restricted latent class models to map the skill structure of achievement items. Journal of Educational Measurement, 26(4):301–321, 1989.
- R. K. Hambleton, H. Swaminathan, and H. J. Rogers. Fundamentals of item response theory, volume 2. Sage, 1991.
- M. Jaeger. Learning and Reasoning with Graph Data: Neural and Statistical-Relational Approaches. In International Research School in Artificial Intelligence in Bergen (AIB 2022), volume 99 of Open Access Series in Informatics (OASIcs), pages 5:1–5:42, 2022.
- C. S. Jensen, U. Kjærulff, and A. Kong. Blocking gibbs sampling in very large probabilistic expert systems. International Journal of Human-Computer Studies, 42(6):647–666, 1995.
- B. W. Junker and K. Sijtsma. Cognitive assessment models with few assumptions, and connections with nonparametric item response theory. Applied Psychological Measurement, 25(3):258–272, 2001.
- T. Käser, S. Klingler, A. G. Schwing, and M. Gross. Dynamic bayesian networks for student modeling. IEEE Transactions on Learning Technologies, 10(4):450–462, 2017.
- S. Pandey and G. Karypis. A self-attentive model for knowledge tracing. In 12th International Conference on Educational Data Mining, EDM 2019, pages 384–389. International Educational Data Mining Society, 2019.
- P. I. Pavlik, H. Cen, and K. R. Koedinger. Performance factors analysis–a new alternative to knowledge tracing. In Artificial Intelligence in Education, pages 531–538. IOS Press, 2009.
- C. Piech, J. Bassen, J. Huang, S. Ganguli, M. Sahami, L. J. Guibas, and J. Sohl-Dickstein. Deep knowledge tracing. Advances in neural information processing systems, 28, 2015.
- M. D. Reckase. Multidimensional item response theory models. In Multidimensional item response theory, pages 79–112. Springer, 2009.
- R. Schmucker, J. Wang, S. Hu, and T. M. Mitchell. Assessing the performance of online students–new data, new approaches, improved accuracy. Journal of Educational Data Mining, 14(1):1–45, 2022.
- J. L. Templin and R. A. Henson. Measurement of psychological disorders using cognitive diagnosis models. Psychological methods, 11(3):287, 2006.
- S. M. Vieira, U. Kaymak, and J. M. Sousa. Cohen’s kappa coefficient as a performance measure for feature selection. In International conference on fuzzy systems, pages 1–8. IEEE, 2010.
- G. C. Wei and M. A. Tanner. A monte carlo implementation of the em algorithm and the poor man’s data augmentation algorithms. Journal of the American statistical Association, 85(411):699–704, 1990.
APPENDIX
A. KNOWLEDGE COMPONENTS IN THE REAL-WORLD SUB-DATASETS
| Dataset | \(\mathfrak {A}\) | \(\mathfrak {B}\) |
|---|---|---|
| ASSISTments12 | Addition and Subtraction Integers (ASI) | Multiplication and Division Integers (MDI) |
| ASSISTments12 | Addition and Subtraction Fractions (ASF) | Multiplication Fractions (MF) |
| ASSISTments12 | Addition and Subtraction Integers (ASI) | Addition and Subtraction Fractions (ASF) |
| ASSISTments12 | Addition and Subtraction Positive Decimals (ASPD) | Multiplication and Division Positive Decimals (MDPD) |
| ASSISTments12 | Addition and Subtraction Fractions (ASF) | Division Fractions (DF) |
| ASSISTments12 | Addition and Subtraction Integers (ASI) | Exponents (E) |
| Eedi2020 | Factors and Highest Common Factor (FHCF) | Multiples and Lowest Common Multiple (MLCM) |
| Eedi2020 | Factors and Highest Common Factor (FHCF) | Prime Numbers and Prime Factors (PNPF) |
| Eedi2020 | Multiples and Lowest Common Multiple (MLCM) | Prime Numbers and Prime Factors (PNPF) |
| Eedi2020 | Volume of Non-Prisms (VNP) | Mental Multiplication and Division (MMD) |
| Eedi2020 | Volume of Non-Prisms (VNP) | Mental Addition and Subtraction (MAS) |
| Eedi2020 | Mental Addition and Subtraction (MAS) | Mental Multiplication and Division (MMD) |
| Kartable | Determine the canonical form of a quadratic polynomial (CF) | Give the roots of a quadratic polynomial (Solve) |
| Kartable | Determine if a real number is a root of a quadratic polynomial (Root) | Find an obvious root for a quadratic polynomial (OR) |
| Kartable | Give the roots of a quadratic polynomial (Solve) | Determine if a real number is a root of a quadratic polynomial (Root) |
| Kartable | Determine the canonical form of a quadratic polynomial (CF) | Give the sign chart of a quadratic polynomial (Chart) |
| Kartable | Give the roots of a quadratic polynomial (Solve) | Give the sign chart of a quadratic polynomial (Chart) |
| Kartable | Find an obvious root for a quadratic polynomial (OR) | Calculate the discriminant of a quadratic polynomial given in the expanded form (D) |
© 2023 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.