ABSTRACT
The application of machine learning techniques to educational datasets has great potential to improve our understanding of learning processes. However, there are privacy concerns in the community about the datasets and models that are being developed using student interactions. This limits the development of AI in education. Differential privacy provides a mathematical framework that limits what can be inferred about an individual in a data set. In this study, we apply differential privacy techniques to knowledge tracing models and analyze the privacy-utility trade-off across three distinct privacy accounting methods. Our assessment offers insights into the practical challenges of implementing privacy-preserving knowledge tracing. We define differential privacy at the user level, where protection extends to a student’s entire sequence of interactions. Our study shows that knowledge tracing models respond differently to privacy constraints, with deep knowledge tracing models maintaining competitive performance under differential privacy. We address important considerations for application of differential privacy, including optimal hyperparameter selection and evaluation of privacy accounting methods that balance strong privacy guarantees with model performance.
Keywords
1. INTRODUCTION
Working with educational data requires protecting the privacy of the student. The simplest approach is to anonymize the data by removing names, social security numbers, or other direct identifiers. However, such data may still be vulnerable to reidentification methods, which leverage correlations, summary statistics, or other knowledge to infer personal information from anonymized data[5, 17]. For example, in an anonymized dataset of test scores on multiple subjects, someone who knows a student’s score in one subject could use that knowledge to determine their scores in the other subjects. Differential privacy (DP) goes beyond anonymization to provide strong, statistical guarantees for privacy via randomization [4].
DP is widely used in a growing number of industries. Apple leverages local differential privacy to enhance user-level privacy in personalized services such as suggestions and health analytics applications. Microsoft incorporates DP in its Azure platform, which enables privacy-preserving data analysis for cloud-based services. The US Census Bureau also uses DP techniques to protect the confidentiality of respondents, as part of the new Disclosure Avoidance system. The implementation adds controlled noise at different geographic levels and demonstrates how privacy protection can be applied while maintaining the utility of demographic analysis [18].
In this paper, we investigate the application of DP to educational data mining, focusing specifically on knowledge tracing. Knowledge tracing is the task of modeling student knowledge states from their interaction history to predict performance on future questions. This is a core task in educational data mining with applications in adaptive learning systems, personalized feedback, and educational resource optimization.
Numerous studies investigate potential threat scenarios in learning analytics, including risks of re-identifying individuals in educational datasets [26, 22, 24, 14, 21, 10, 23]. Others explore various perturbation approaches in differential privacy [13]. However, very little of this work focuses on specific applications, such as knowledge tracing, or the unique challenges of applying differential privacy to deep learning in education. Knowledge tracing is different from other differential privacy settings because of the dynamic, sequential nature of knowledge tracing tasks, where each interaction potentially reveals sensitive information about a student’s learning progress and cognitive states. We address this gap by examining the unique challenges of applying differential privacy to knowledge tracing tasks by examining a broader spectrum of differential privacy theories and techniques. Our research makes several distinct contributions.
-
We discuss how differential privacy can be applied to the knowledge tracing setting, including defining the problem formally.
-
We use existing tools to implement differentially private versions of three knowledge tracing methods: (1) BKT [25], a well-established probabilistic learner modeling approach; (2) DKT [19], which uses recurrent neural networks to capture complex patterns in student interaction sequences; and (3) MonaCoBERT [11], a transformer-based approach that leverages contextual representations for knowledge tracing.
-
We evaluate private knowledge tracing methods on six datasets in order to (1) determine which private method is most accurate; (2) compare the performance of private and non-private methods; (3) explore the tradeoff between greater privacy (smaller epsilon) and greater accuracy (higher AUC); (4) compare the guarantees offered by different DP accounting methods, namely Privacy Random Variable, Rényi Differential Privacy, and Gaussian Differential Privacy(GDP).
Overall, our findings show that we can offer DP guarantees for knowledge tracing, with DKT offering the strongest performance overall and performing nearly as well in the private setting as in the non-private setting (for \(\varepsilon < 8\)).
2. DP KNOWLEDGE TRACING
We now provide brief background on differential privacy (DP), while explaining how these concepts can be applied to the knowledge tracing setting.
2.1 Differential Privacy
The definition of differential privacy [4] centers around the notion of neighboring datasets, where \(D\) and \(D'\) belong to the set \(\mathcal {S}\) of all Datasets. The probability of a specific event resulting from a query on the dataset \(D\) is compared to the outcome for a query on dataset \(D'\). Differential privacy ensures that these probabilities differ by at most a factor of \(e^\varepsilon \), making it infeasible to distinguish whether an individual’s data was included or excluded based solely on the query results. Therefore, the privacy level is quantified by the exponential privacy parameter \(\varepsilon \), a non-negative real number that measures the degree of privacy protection.
Definition 1. A mechanism \(\mathcal {M}\) is \((\varepsilon , \delta )\)-differentially private if for all pairs of adjacent datasets \(D\) and \(D'\), where \(D'\) differs from \(D\) by one data point \(x\), and for all subsets \(S \subseteq \text {Range}(\mathcal {M})\), the following inequality holds:
The \(\delta \) term accounts for privacy failures in ways that cannot be accounted for in \(\varepsilon - DP\) . The \(\delta \) represents a small probability of exceeding the privacy loss bound set by \(\varepsilon \).[1][16].
This definition turns out to have many nice mathematical properties, which has made it a popular framework for analyzing privacy. One of those properties is sequential composition:
Theorem 1 (Sequential Composition). If \(F_1(x)\) satisfies \(\varepsilon _1\)-differential privacy, and \(F_2(x)\) satisfies \(\varepsilon _2\)-differential privacy, then the mechanism \(G(x) = (F_1(x), F_2(x))\) satisfies \((\varepsilon _1 + \varepsilon _2)\)-differential privacy [4].
This means that when multiple queries are performed on the same dataset, the total privacy budget is the sum of the individual budgets.
2.2 Problem Definition
We now discuss how DP can be applied to knowledge tracing. The knowledge tracing task aims to model a student’s evolving knowledge state from their interaction history. The knowledge tracing task can be formalized as follows: given a sequence of observed student interaction consisting of questions \(q_i\) and responses \(r_i\), the objective is to estimate the student’s latent knowledge state to predict their correct/incorrect answers on subsequent questions. Specifically, given a test-set of users’ question and response sequences \(y_{s,q} \in \{0,1\}\) and predictions \(\hat {p}_{s,q}\) from the model, the task is to predict the probability of a correct response for the next question in the sequence based on previous performance.
Model performance is evaluated through binary classification metrics, where Area Under the ROC Curve (AUC) quantifies the model’s ability to discriminate between correct and incorrect responses. Root Mean Square Error (RMSE) is used to measure the magnitude of the prediction error on the test set. The key difference in making knowledge tracing private is to precisely define the guarantee we’re seeking to enforce. For standard DP definitions, the two datasets \(D\) and \(D'\) being compared differ in a single element \(x\); for DP knowledge tracing, we consider two datasets that differ in a single user, including all of their answers: Definition 2. A knowledge tracing mechanism \(\mathcal {M}\) is \((\varepsilon , \delta )\)-differentially private if for all pairs of adjacent datasets \(D\) and \(D'\), where \(D'\) differs from \(D\) by the addition or removal of one user’s entire sequence of interactions \((q_1, r_1) \dots (q_i, r_i)\), and for all subsets \(S \subseteq \text {Range}(\mathcal {M})\), the following inequality holds:
Therefore, knowledge tracing can be defined as a randomized mechanism that adheres to \((\varepsilon , \delta )\) -differential privacy.
This turns out to be a very strong definition of privacy, one that works even against an attacker who knows every single student in the dataset \(D\) and the hypothetical student that might or might not be in the dataset \(D'\).
2.3 Moments Accountant
We now briefly describe the moments accountant method, a foundational privacy accounting technique, that yields better bounds for deep learning [2].
The privacy loss random variable (3) quantifies how output probabilities of mechanisms differ between adjacent datasets \(d\) and \(d'\).
Definition 3. For neighboring datasets \(d, d'\), a mechanism \(\mathcal {M}\), auxiliary input \(aux\), and outcome \(o\), the privacy loss is defined as:
2.4 Rènyi Differential Privacy
Rényi Differential Privacy(RDP) [15] provides a theoretical framework for privacy accounting, formalizing the concept of moments accountant method. RDP measures privacy loss using Rényi divergence between output distributions. Definition 4. For probability distributions \(P\) and \(Q\), the Rényi divergence of order \(\alpha > 1\) is defined as:
This approach provides tight composition bounds and allows tracking privacy budget during training.
3. EMPIRICAL EVALUATION
3.1 Datasets
Six benchmark datasets were used in training knowledge tracing tasks. The ASSISTments datasets are an extensive collection of anonymized student data from the ASSISTments learning platform [7], for selected school years 1. The datasets adhere to privacy protocols, with the personally identifiable information removed. The Algebra datasets were a part of the 2010 KDD Cup Educational Data Mining Challenge 2. The competition included two Algebra developmental datasets for two separate academic years. EdNET consists of large scale student interaction logs collected from Scala, an intelligent tutoring system [3]. Knowledge tracing datasets typically contain fields that capture various aspects of student interactions with educational platforms. These generally include student identifiers and unique IDs for questions or exercises attempted. An important field is skill or knowledge component, which links each problem to specific concepts or topics. Each interaction may have specific time stamps and correctness indicating performance.
3.2 Procedure
We evaluate a standard BKT model on the six datasets. The evaluation uses procedures described in the literature[19] [9], using five-fold cross-validation and computing single AUC values from accumulated predictions. The parameters of the Bayesian Knowledge Tracing model, an instance of Hidden Markov Model, used in Yudelson, Koedinger, and Gordon [25] are \(\lambda = \{\Pi , A, B\}\) where \(\Pi \) is the Priors matrix, \(A\) is the Transitions matrix, and \(B\) is the Emissions matrix. The model is defined by two key probability distributions that describe the probability of transitioning between states and the probability of observations from states. These parameters are optimized to maximize the likelihood of observed student performance data, enabling the model to track students’ knowledge states and predict performance. We train BKT on a per-skill basis, treating each skill’s data as an independent set. If we have \(K\) disjoint datasets \(\mathcal {D}_1, \mathcal {D}_2, \dots , \mathcal {D}_K\), where each dataset \(\mathcal {D}_k\) contains distinct and non-overlapping data, and each dataset \(\mathcal {D}_k\) is independently analyzed with a mechanism satisfying \(\varepsilon _k\)-differential privacy, then the privacy budget for the overall dataset \(\mathcal {D} = \bigcup _{k=1}^K \mathcal {D}_k\) remains the same as the privacy budget for each individual dataset. That is,
If all mechanisms are run with the same privacy parameter \(\varepsilon \), then:
3.3 Results and Discussion
We evaluated four models across six datasets, comparing their performance in private and non-private settings. Results for all datasets are shown in Table 1. Deep Knowledge Tracing (DKT) emerged as the best performer across most datasets. The model was trained for 600 epochs with a gradient clipping threshold of 0.5 and a noise multiplier of 6.0, consistently achieving privacy budgets around 7. Both DKT and DKT+ exhibit minimal degradation under differentially private settings.

| KT Models | Non-private | Private
| |||
|---|---|---|---|---|---|
| AUC | RMSE | AUC | RMSE | \(\varepsilon \) | |
| BKT | 0.71 | 0.4147 | 0.69 | 0.5761 | 7.15 |
| DKT | 0.80 | 0.4073 | 0.79 | 0.4527 | 6.46 |
| DKT+ | 0.80 | 0.4195 | 0.78 | 0.4928 | 6.23 |
| MonaCoBERT | 0.79 | 0.4136 | 0.75 | 0.4453 | 6.81 |
| KT Models | Non-private | Private
| |||
|---|---|---|---|---|---|
| AUC | RMSE | AUC | RMSE | \(\varepsilon \) | |
| BKT | 0.62 | 0.6145 | 0.57 | 0.5935 | 8.25 |
| DKT | 0.71 | 0.5558 | 0.70 | 0.5748 | 7.12 |
| DKT+ | 0.70 | 0.5476 | 0.70 | 0.5621 | 6.74 |
| MonaCoBERT | 0.77 | 0.4532 | 0.71 | 0.4872 | 6.81 |
| KT models | Non-private | Private
| |||
|---|---|---|---|---|---|
| AUC | RMSE | AUC | RMSE | \(\varepsilon \) | |
| BKT | 0.59 | 0.6236 | 0.54 | 0.6672 | 8.14 |
| DKT | 0.72 | 0.4765 | 0.70 | 0.4784 | 7.15 |
| DKT+ | 0.72 | 0.4462 | 0.71 | 0.4622 | 6.95 |
| MonaCoBERT | 0.71 | 0.4340 | 0.68 | 0.4776 | 7.85 |
| KT models | Non-private | Private
| |||
|---|---|---|---|---|---|
| AUC | RMSE | AUC | RMSE | \(\varepsilon \) | |
| BKT | 0.64 | 0.5715 | 0.59 | 0.5927 | 7.95 |
| DKT | 0.72 | 0.5754 | 0.69 | 0.6012 | 7.22 |
| DKT+ | 0.73 | 0.5681 | 0.69 | 0.6125 | 7.55 |
| MonaCoBERT | 0.81 | 0.5449 | 0.68 | 0.5421 | 7.18 |
| KT models | Non-private | Private
| |||
|---|---|---|---|---|---|
| AUC | RMSE | AUC | RMSE | \(\varepsilon \) | |
| BKT | 0.70 | 0.4285 | 0.69 | 0.5065 | 6.99 |
| DKT | 0.80 | 0.4634 | 0.78 | 0.4865 | 7.45 |
| DKT+ | 0.80 | 0.4372 | 0.78 | 0.4741 | 6.96 |
| MonaCoBERT | 0.80 | 0.4382 | 0.74 | 0.4886 | 6.72 |
| KT models | Non-private | Private
| |||
|---|---|---|---|---|---|
| AUC | RMSE | AUC | RMSE | \(\varepsilon \) | |
| BKT | 0.71 | 0.5105 | 0.68 | 0.5467 | 6.99 |
| DKT | 0.81 | 0.4552 | 0.79 | 0.3932 | 6.21 |
| DKT+ | 0.80 | 0.4671 | 0.78 | 0.4210 | 7.62 |
| MonaCoBERT | 0.81 | 0.3928 | 0.75 | 0.3425 | 6.20 |
In the non-private setting, the deep learning methods demonstrate strong predictive performance. For the Assistments2009 dataset, DKT achieved an AUC of 0.80 in the non-private setting and maintained a competitive AUC of 0.79 when privacy-preserving constraints were applied. Similar trends were observed for Assistments 2017 and Assistments 2017, where DKT achieved an AUC of 0.75 in both private and non-private settings. The model also showed promising results on EdNet, achieving an AUC of 0.72 non-private and 0.69 in private setting. The results demonstrate that Deep Knowledge Tracing, which leverages recurrent neural networks to model student performance, can maintain strong predictive capability under differential privacy. Differentially private DKT-plus shows performance comparable to DKT. In the Assistments2009 dataset, it achieves the same AUC of 0.80 in non-private settings and 0.78 under privacy constraints. For experiments under non-private settings, MonaCoBERT shows consistent performance with AUC scores ranging from 0.71 to 0.81 and 0.68 to 0.75 in private settings. Therefore, the results indicate that DKT and DKT+ are resilient to differential privacy constraints. MonaCoBERT, despite achieving strong performance in non-private settings, experiences a large decline in AUC.
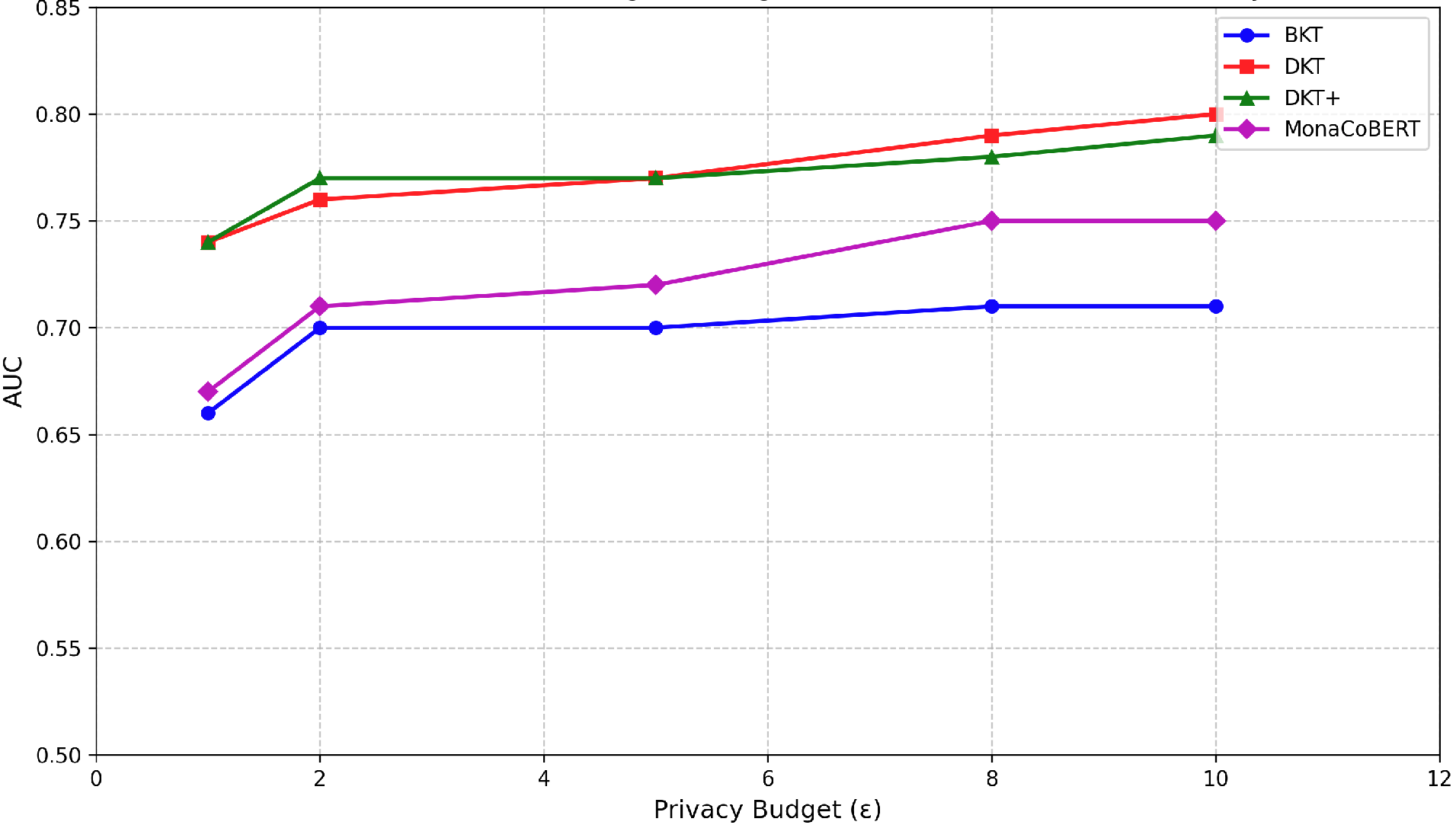
Figure 1 demonstrates the performance of the models under privacy constraints, \(\varepsilon =1.0\) through \(10.0\). In this method, a target privacy budget \(\varepsilon \) is specified, and Opacus adjusts the noise multiplier \(\sigma \) during training to achieve the desired privacy level. The relationship between epsilon \(\varepsilon \) and model performance using three different privacy accounting methods: Rényi Differential Privacy, Gaussian Differential Privacy, and Privacy Random Variable are shown in Figure 2. The graph tracks the three accounting mechanisms over 600 training epochs, revealing different relative budgets. Previous literature [6] has shown that GDP tends to underestimate privacy budgets and the graph shows that GDP reports lower epsilon values overall compared to RDP to achieve the same AUC. Although RDP exhibits slightly conservative privacy budget estimates, it provides a more reliable option to calculate the privacy guarantee through its tighter composition bounds.
4. CONCLUSION
In this work, we implement differential privacy with a focus on user-level sequence protection. We demonstrated that good privacy guarantees can coexist with utility. We employ several privacy accounting techniques to compare cumulative privacy losses. Empirical results in educational datasets demonstrated a reasonable trade-off in AUC and privacy budgets. This study provides a foundation for privacy-preserving knowledge tracing. This paves the way for a wider application of privacy-preserving AI in education.
5. REFERENCES
- EUROCRYPT’06: Proceedings of the 24th annual international conference on The Theory and Applications of Cryptographic Techniques, Berlin, Heidelberg, 2006. Springer-Verlag.
- M. Abadi, A. Chu, I. Goodfellow, H. B. McMahan, I. Mironov, K. Talwar, and L. Zhang. Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, CCS’16. ACM, Oct. 2016.
- Y. Choi, Y. Lee, D. Shin, J. Cho, S. Park, S. Lee, J. Baek, C. Bae, B. Kim, and J. Heo. Ednet: A large-scale hierarchical dataset in education. In Artificial Intelligence in Education: 21st International Conference, AIED 2020, Ifrane, Morocco, July 6–10, 2020, Proceedings, Part II 21, pages 69–73. Springer, 2020.
- C. Dwork and A. Roth. The Algorithmic Foundations of Differential Privacy. Foundations and Trends® in Theoretical Computer Science Series. Now Publishers, 2014.
- A. Gadotti, L. Rocher, F. Houssiau, A.-M. Creţu, and Y.-A. de Montjoye. Anonymization: The imperfect science of using data while preserving privacy. Science Advances, 10(29):eadn7053, 2024.
- S. Gopi, Y. T. Lee, and L. Wutschitz. Numerical composition of differential privacy. Advances in Neural Information Processing Systems, 34:11631–11642, 2021.
- N. Heffernan and C. Heffernan. The assistments ecosystem: Building a platform that brings scientists and teachers together for minimally invasive research on human learning and teaching. International Journal of Artificial Intelligence in Education, 24, 12 2014.
- B. Jayaraman and D. Evans. Evaluating differentially private machine learning in practice, 2019.
- M. Khajah, R. V. Lindsey, and M. C. Mozer. How deep is knowledge tracing?, 2016.
- M. Klose, V. Desai, Y. Song, and E. F. Gehringer. Edm and privacy: Ethics and legalities of data collection, usage, and storage. In Educational Data Mining, 2020.
- U. Lee, Y. Park, Y. Kim, S. Choi, and H. Kim. Monacobert: Monotonic attention based convbert for knowledge tracing. In International Conference on Intelligent Tutoring Systems, pages 107–123. Springer, 2024.
- X. Li, F. Tramer, P. Liang, and T. Hashimoto. Large language models can be strong differentially private learners. arXiv preprint arXiv:2110.05679, 2021.
- Q. Liu, R. Shakya, M. Khalil, and J. Jovanovic. Advancing privacy in learning analytics using differential privacy. In Proceedings of the 15th International Learning Analytics and Knowledge Conference, LAK ’25, page 181–191, New York, NY, USA, 2025. Association for Computing Machinery.
- R. Marshall, A. Pardo, D. Smith, and T. Watson. Implementing next generation privacy and ethics research in education technology. British Journal of Educational Technology, 53(4):737–755, 2022.
- I. Mironov. Rényi differential privacy. In 2017 IEEE 30th computer security foundations symposium (CSF), pages 263–275. IEEE, 2017.
- I. Mironov, O. Pandey, O. Reingold, and S. Vadhan. Computational differential privacy. In S. Halevi, editor, Advances in Cryptology - CRYPTO 2009, pages 126–142, Berlin, Heidelberg, 2009. Springer Berlin Heidelberg.
- A. Narayanan and V. Shmatikov. Robust de-anonymization of large sparse datasets. In 2008 IEEE Symposium on Security and Privacy (sp 2008), pages 111–125, 2008.
- S. Petti and A. Flaxman. Differential privacy in the 2020 us census: what will it do? quantifying the accuracy/privacy tradeoff. Gates Open Research, 3:1722, 12 2019.
- C. Piech, J. Spencer, J. Huang, S. Ganguli, M. Sahami, L. Guibas, and J. Sohl-Dickstein. Deep knowledge tracing, 2015.
- N. Ponomareva, H. Hazimeh, A. Kurakin, Z. Xu, C. Denison, H. B. McMahan, S. Vassilvitskii, S. Chien, and A. G. Thakurta. How to dp-fy ml: A practical guide to machine learning with differential privacy. Journal of Artificial Intelligence Research, 77:1113–1201, July 2023.
- J. R. Reidenberg and F. Schaub. Achieving big data privacy in education. Theory and Research in Education, 16(3):263–279, 2018.
- D. Vatsalan, T. Rakotoarivelo, R. Bhaskar, P. Tyler, and D. Ladjal. Privacy risk quantification in education data using markov model. British Journal of Educational Technology, 53(4):804–821, 2022.
- J.-J. Vie, T. Rigaux, and S. Minn. Privacy-preserving synthetic educational data generation, 2022.
- S. Xu and X. Yin. Recommendation system for privacy-preserving education technologies. Computational Intelligence and Neuroscience, 2022(1):3502992, 2022.
- M. V. Yudelson, K. R. Koedinger, and G. J. Gordon. Individualized bayesian knowledge tracing models. In H. C. Lane, K. Yacef, J. Mostow, and P. Pavlik, editors, Artificial Intelligence in Education, pages 171–180, Berlin, Heidelberg, 2013. Springer Berlin Heidelberg.
- C. Zhan, S. Joksimović, D. Ladjal, T. Rakotoarivelo, R. Marshall, and A. Pardo. Preserving both privacy and utility in learning analytics. IEEE Transactions on Learning Technologies, 17:1615–1627, 2024.
https://anonymous.4open.science/r/Differentially-Private-Knowledge-Tracing-FB29/README.md
1https://sites.google.com/site/assistmentsdata/home/2009-2010-assistment-data
2https://pslcdatashop.web.cmu.edu/KDDCup
© 2025 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.