ABSTRACT
In this paper, we introduce a novel approach to automate course equivalency evaluation across multiple colleges using publicly available data, deep embedding models, and traditional machine learning. The current process of determining course equivalency is labor-intensive, requiring manual assessment of course descriptions or syllabi, which is inefficient and could cause delays for students matriculating into a school. We leverage deep learning to generate semantic embeddings from raw course descriptions retrieved from school websites and then apply traditional machine learning to classify course equivalence. Our findings demonstrate that this automated approach can significantly improve upon existing manual processes, achieving an \(F_1\)-score between \(0.971\) and \(0.996\). Moreover, the flexibility of embeddings permits expanded applications such as semantic search and retrieval-augmented generation while reducing computational cost.
Keywords
1. INTRODUCTION
Matriculating students between institutions requires a labor-intensive evaluation from advisors who are well versed in the nuances of course learning outcomes. This process involves the manual assessment of course descriptions and/or syllabi to determine whether a particular course from one college may be directly transferable to another course that is offered at the receiving college. These challenges are compounded by varying accreditation standards across disparate entities and the diverse program objectives that make it difficult to match equivalent courses [15]. Furthermore, educational standards and curricula outside of the U.S. introduce yet another layer of complexity to this already demanding task.
The consequences of incorrect execution of course equivalency evaluations can be substantial, potentially delaying student progress and even forcing them to retake courses already completed. This challenge is particularly acute given the State of California’s especially complex public higher education system, which consists of three public school systems: University of California (UC), California State University ( CSU), and California Community Colleges (CCC) [6]. In 2023, these three systems served nearly 2.9 million students [20, 4, 3] and nearly 588,000 students enrolled in California community colleges transferred into four-year university programs within six years [6].
The process of matriculating students transferring from one California college to another consists of consulting articulation agreements through Assist.org, the official course transfer and articulation system for California’s public colleges and universities [1]. This system relies on manual updates by college administrators who must evaluate individual courses, making it an inefficient and slow process. Because all 149 colleges and universities within the California higher education system have to handle the course pairings for every discipline from every other possible originating campus, the current process often leads to delays and may result in inaccurate or outdated information for students.
While this problem has seen some attention in prior work, a comprehensive and scalable solution remains elusive. Previous efforts have relied on using private data and custom algorithms. In our previous work, we have explored the application of prompt engineering and in-context learning with large language models to determine course equivalency by using publicly available course descriptions [12]. While the results were promising, the alternative solution proposed in this paper offers increased flexibility, reduced computational costs, and significantly improved accuracy. For example, the embedding-based \(k\)-NN algorithm achieves an \(F_1\)-score between 0.971 and 0.996.
The following sections will outline related research and our own efforts, provide an overview of our data, methodologies, and evaluation metrics, discuss our preliminary findings and analysis, and conclude by considering future research possibilities and potential applications of our work.
| Model Name | Rank\(^{*}\) | Params\(^{\dagger }\) | Dims | Acc |
|---|---|---|---|---|
| GIST-small-Embedding-v0 | 41 | 33 | 384 | 0.9759 |
| bge-small-en-v1.5 | 47 | 33 | 384 | 0.9670 |
| GIST-Embedding-v0 | 33 | 109 | 768 | 0.9768 |
| bge-base-en-v1.5 | 35 | 109 | 768 | 0.9732 |
| gte-base-en-v1.5 | 31 | 137 | 768 | 0.9732 |
| mxbai-embed-large-v1 | 24 | 335 | 1024 | 0.9759 |
| gte-large-en-v1.5 | 21 | 434 | 1024 | 0.9777 |
| multilingual-e5-large-inst | 34 | 560 | 514 | 0.9670 |
| stella_en_1.5B_v5 | 3 | 1543 | 8192 | 0.9857 |
| SFR-Embedding-2_R | 4 | 7111 | 4096 | 0.9839 |
| Agte-Qwen2-7B-instruct | 5 | 7613 | 3584 | 0.9804 |
| nvidia/NV-Embed-v2 | 1 | 7851 | 4096 | 0.9831 |
| \(^{*}\) Huggingface Overall Leaderboard Rank
| ||||
| \(^{\dagger }\) in Millions | ||||
2. RELATED WORK
2.1 Applications of Semantic Embeddings
The emergence of Large Language Models (LLMs) and their ability to process free-form text has brought substantial growth in the automation of tasks involving text analysis and understanding, but requires significant compute and energy resources [27]. Despite finding increased popularity in applications such as semantic retrieval [11], similarity search [13], and various other tasks [14], the alternative case of using semantic vector representations has remained relatively understudied [22].
2.2 Traditional Machine Learning
Traditional machine learning (ML) consists of a vast set of tools to understand data that dates back to 1936 [9]. Applying ML techniques such as regression, support vector machines, and random forests to semantic embeddings as features may lead to improved performance in tasks such as text classification and similarity analysis. Since deep embeddings have been found to be dimensionally robust, ML performance may remain strong even when evaluating high-dimensional data [22]. With the vast diversity of course subject matter, deep embeddings have a great potential to maintain the context of course descriptions beyond what is possible with traditional representations.
2.3 Educational Data Mining (EDM)
Within the domain of Educational Data Mining (EDM), technological advancements spurred the use of technology and data collection in education [2]. Machine learning is regularly applied to address issues such as student dropout and graduation prediction [26], course recommendation [16, 7, 18, 10], and curricular design [19, 25]. This study complements content-based course recommendation by preventing redundant course selections, thus facilitating personalized academic planning.
3. METHODS AND ALGORITHMS
An initial analysis of various open-source deep-learning embedding models was completed to discern whether there was a significant difference between models. See Table 1 for this list of models and their respective characteristics. Next, we selected a dataset of equivalent and non-equivalent courses from 63 college campuses throughout California with a total of 228 courses. A labeled dataset of equivalent and non-equivalent course pairs was then generated. It was with this data that we then used the deep-learning embedding models to generate semantic vector embeddings. Finally, a difference vector was created from each pair, which provided us with the feature vectors that were subsequently used to train a host of traditional machine learning classifiers. See Figure 2 for a diagram illustrating the methods applied.
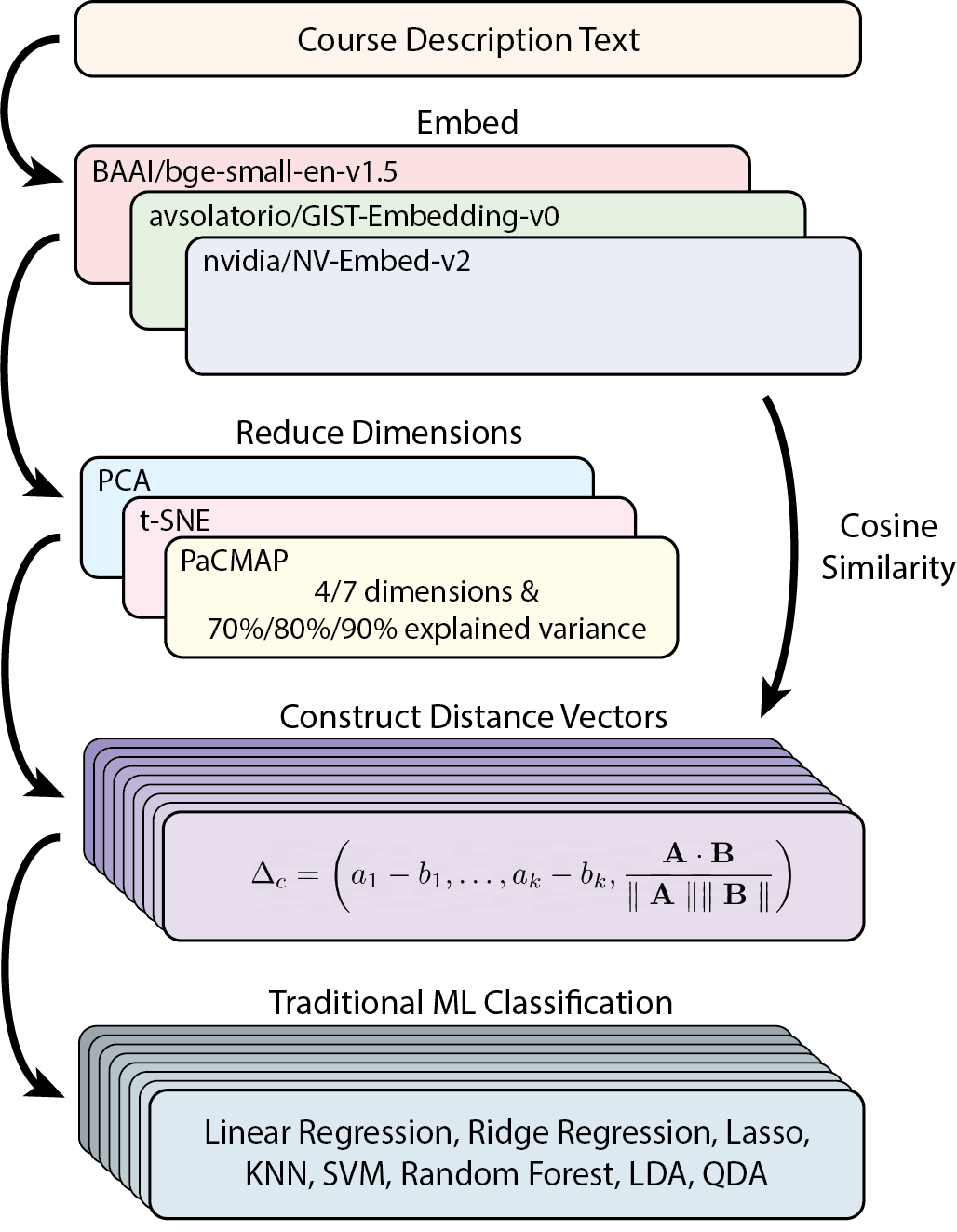
3.1 Data Overview
Five required lower-division courses for the Computer Science major (Calculus I, Discrete Math, Machine Structures, Intro to Programming, and Data Structures) were selected from San Francisco State University (SFSU). These courses were chosen to provide a sufficiently difficult evaluation set. Using Assist.org, articulation agreements mapping these courses to SFSU from other California colleges and universities were gathered.
Course descriptions were manually collected from their corresponding college websites. This course data was copied completely and included: department codes; course codes; titles; descriptions; metadata (e.g. prerequisite requirements, unit count, and grading options); and special characters (e.g. punctuation and line breaks). Assuming symmetry and transitivity for equivalent courses, course descriptions were then paired up with equivalent and non-equivalent courses, with a final set of 5660 equivalent and 5660 non-equivalent course pairs.
3.2 Distance Metric
Although cosine similarity is often used on embeddings to distinguish and rank texts according to semantic similarity [21], finding an appropriate decision boundary and threshold for equivalency is not feasible. A ranked cosine similarity search only produces relative similarities, and does not provide enough insight to make an informed decision about whether two courses are interchangeable. This method could work for courses that are highly dissimilar, but would not be suitable for nuanced decisions for courses that may be similar, but not equivalent.
Because of this major disadvantage, we propose a simple, yet powerful distance measure that captures local and global disparities in course embedding spaces. Our distance measure \(\Delta = f\left (\mathbf {A}, \mathbf {B}\right )\), with \(\mathbf {A}, \mathbf {B}\in \mathbb {R}^k\) as embedded features of course texts of dimension \(k\), captures local and global differences. We then construct our distance vector by concatenating the elementwise differences to the cosine similarity as follows:
where \(\mathbf {A} = (a_1, \dots , a_k)\) and \(\mathbf {B} = (b_1, \dots , b_k)\). This measure was chosen for its simplicity and effectiveness at improving the results of linear classifiers (Figure 2). Each of these feature vectors were then labeled with respect to their equivalency. An ablation study was also performed to determine the effect of omitting cosine similarity, which we denote as \(\Delta _l\). Various dimensionality reduction techniques were also employed for both exploratory data analysis and equivalency evaluation.
With the distance measures calculated, an 80/20 training and validation split was applied and a hyperparameter grid search using 5-fold cross-validation (CV) of the training set for all the models was completed.
3.3 Models
Our approach began with a preliminary analysis of a variety of open-source deep-learning embedding models as shown in Table 1. This analysis was completed by evaluating the similarity between positive (i.e. equivalent) and negative (i.e. non-equivalent) pairs; the model is correct if the similarity between the anchor and an equivalent course text was greater than the similarity between the anchor and a non-equivalent course text. This evaluation was sufficient enough to help narrow down the list of models for further study. With preliminary results showing relatively close scores across all the embedding models under consideration (sample accuracy \(\overline {x} = 0.9767\) and \(s_x = 0.00605\)), we selected “bge-small-en-v1.5” (BGE), “GIST-Embedding-v0” (GIST), and “NV-Embed-v2” (NVE), representing small, medium, and large parameter size categories, respectively (see Table 2 for details).
| Explained Variance
| |||||
|---|---|---|---|---|---|
| # of Parameters | Embedding | (# of PCs)
| |||
| Model Name | (in Millions) | Dimensions | 70% | 80% | 90% |
| BAAI/bge-small-en-v1.5 | 33 | 384 | 28 | 45 | 76 |
| avsolatorio/GIST-Embedding-v0 | 109 | 768 | 23 | 40 | 73 |
| nvidia/NV-Embed-v2 | 7851 | 4096 | 20 | 37 | 73 |
Within the domain of machine learning the “curse of dimensionality” has been well documented [17, 23, 5]. Our dataset of 11,320 observations should be sufficient for both of the smaller embedding models, but could pose a problem when using NVE, which uses 4096 dimensions. To empirically verify how dimensionality reduction may affect the classification results, we applied principal component analysis (PCA), t-distributed stochastic neighbor embedding (t-SNE), and Pairwise Controlled Manifold Approximation (PaCMAP), to the embeddings [24].
Towards this end, we first applied PCA and calculated the the number of principal components that had 70%, 80%, and 90% explained variance for each embedding model. Using these values along with 4 and 7 dimensions, we trained each model and tested each of the 8 classification models with the transformed vectors.
Armed with our \(\Delta _c\) and \(\Delta _l\) distance vectors, we proceeded to apply a brute-force hyperparameter grid search using 5-fold CV during training using the following classification models: Logistic Regression (LR), Ridge Regression (Ridge), Lasso, K-Nearest Neighbors (\(k\)-NN), Support Vector Machine (SVM), Random Forest (RF), Linear Discriminant Analysis (LDA), and Quadratic Discriminant Analysis (QDA).
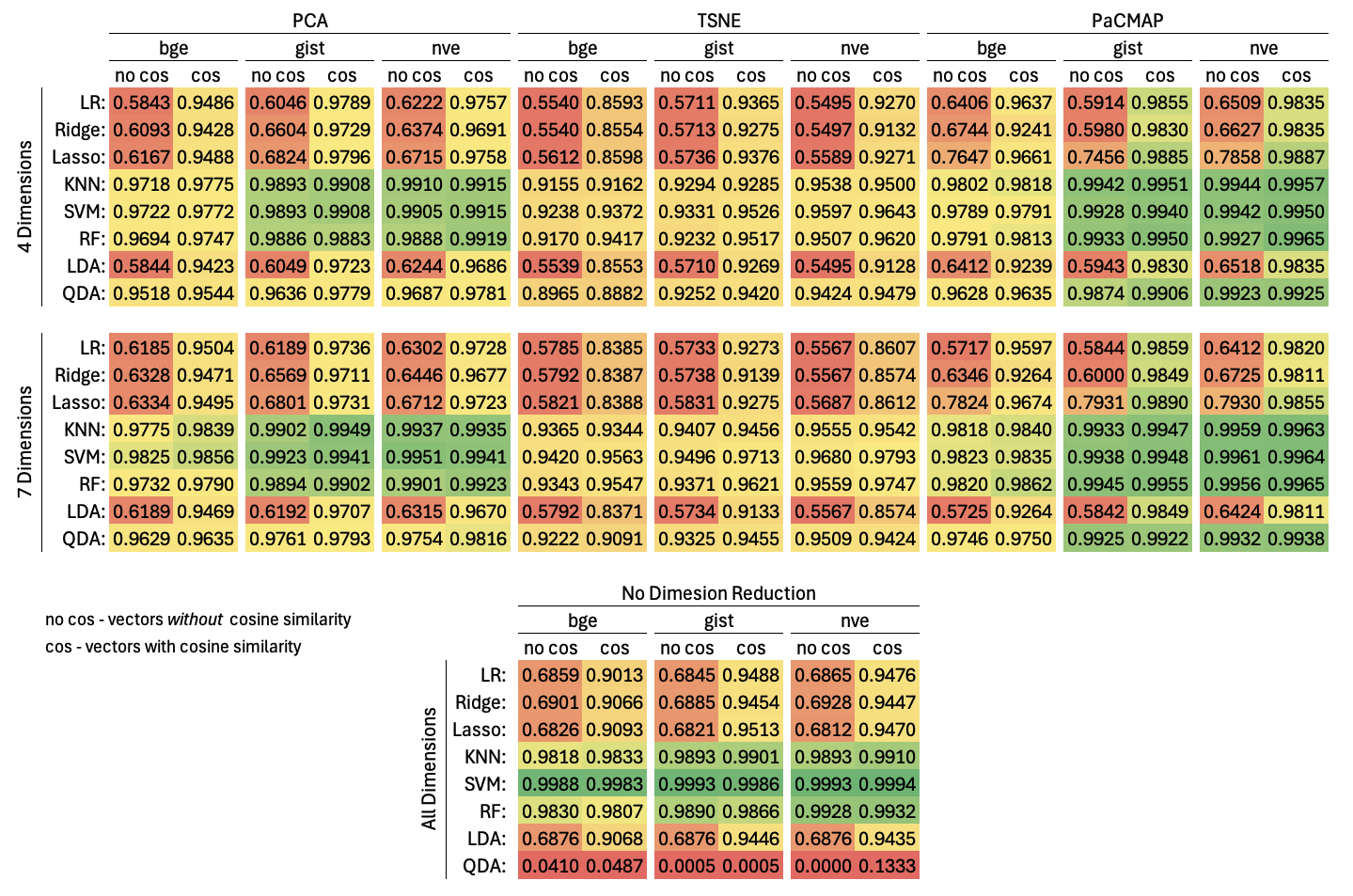
4. RESULTS
We begin by reviewing the performance of linear models. In Figure 2, we show that all linear models (LR, Ridge, Lasso, and LDA) benefitted significantly from the inclusion of cosine similarity in the distance metrics (\(p\textrm {-val} \in [7.71\times 10^{-16}, 6.92\times 10^{-15}]\)). Whether dimensionality reduction made a significant difference depends on your choice of \(p\textrm {-val}\) threshold (\(p\textrm {-val} \in [0.062, 0.096]\)), but the models suffered an overall reduction in performance when t-SNE was applied (\(p\textrm {-val} \in [1.63\times 10^{-12}, 1.63\times 10^{-12}]\)).
Non-linear models (\(k\)-NN, SVM, RF, and QDA), on the other hand, generally fared better than the linear models (\(p\textrm {-val} \in [1.11\times 10^{-5}, 0.053]\)), and were not significantly influenced by the inclusion or omission of cosine similarity (\(p\textrm {-val} \in [0.315, 0.962]\)). Unlike the linear models, dimensionality reduction generally impacted performance negatively (\(p\textrm {-val} \in [0.0014, 0.012]\)), with QDA clearly being positively impacted by dimensionality reduction. Nevertheless, the QDA results look suspicious and warrant further examination.
Out of all the traditional machine learning classification models, we found the most success with \(k\)-NN, SVM, and RF. These three models boasted \(F_1\)-scores ranging between \(0.916\) at the worst to \(0.999\) at the best, with SVM yielding the most impressive classification performance of the three (Figure 2). There are computation, memory, outlier sensitivity, dimensionality, and training factors to consider for each model [8], but the balance afforded by \(k\)-NN and RF suggests that they are the most suitable choices for future research in this application.
5. LIMITATIONS & FUTURE WORK
Despite promising results, the dataset used is limited and only contains a small set of courses articulated to SFSU. In addition, the assumption of symmetry and transitivity likely does not hold in the real world. For example, a business Calculus course will likely not be sufficient to satisfy an engineering-focused Calculus course, but the reverse would. Another set of cases that were omitted from this dataset were many-to-many and many-to-one course equivalency relations. We have obtained an expanded dataset that includes many more campuses and disciplines, so the dataset limitation will be addressed soon. Another area to explore would be various distance measures beyond our chosen one; the effectiveness at simply concatenating cosine similarity to the embeddings produced significant improvements with linear classifiers, so exploring other methods of measuring differences between embeddings could prove fruitful. One final area of investigation to be completed is exploring task-optimized fine-tuning of embedding models to evaluate whether such optimized models may produce even better results than those produced so far.
6. DISCUSSION
Applying traditional machine learning techniques with semantic embeddings as feature sets may provide an alternative to computationally expensive foundation models. In addition, embeddings can be stored, reducing the redundancy of repeated computation, which facilitates more efficient last-mile classification. Beyond just pairwise course equivalency evaluation, the flexibility of embeddings promotes other applications such as semantic search and retrieval augmented generation. Thus, finding courses by subject matter, general education requirement attributes, and many more applications could be unlocked with the use of semantic embeddings.
Small task-optimized embedding models could perform as well as (or better than) the larger embedding models used in this study. For example, as shown in Figure 1, the smallest embedding model (BGE) exhibits similar and sometimes better performance when compared with the two larger models. Although large language models are extremely powerful and have been shown to exhibit surprising reasoning capabilities, it is important to select and use the right model for the right task. Applying such models arbitrarily require tremendous amounts of compute and energy to run it. By carefully choosing our methods, we can benefit from the state-of-the-art discoveries without brute-forcing technologies best suited for more complicated tasks.
7. ACKNOWLEDGMENTS
Special thanks go to the Program Pathways Mapper team, which includes representatives from the Kern Community College District, the Foundation for California Community Colleges, and the California Community Colleges Chancellor’s Office.
8. REFERENCES
- Frequently Asked Questions — resource.assist.org. https://resource.assist.org/FAQ. [Accessed 18-03-2025].
- L. Barbeiro, A. Gomes, F. B. Correia, and J. Bernardino. A review of educational data mining trends. Procedia Computer Science, 237:88–95, 2024. International Conference on Industry Sciences and Computer Science Innovation.
- California Community Colleges Chancellor’s Office. Management Information Systems Data Mart, 2024.
- California State University Office of the Chancellor. Enrollment, 2024.
- B. Chandrasekaran and A. Jain. Quantization complexity and independent measurements. IEEE Transactions on Computers, C-23(1):102–106, 1974.
- K. Cook. California’s higher education system, 2024.
- A. Esteban, A. Zafra, and C. Romero. A hybrid multi-criteria approach using a genetic algorithm for recommending courses to university students. In International Educational Data Mining Society, 2018, 2018.
- T. Hastie, R. Tibshirani, and J. Friedman. The Elements of Statistical Learning. Springer Series in Statistics. Springer New York Inc., New York, NY, USA, 2001.
- G. James, D. Witten, T. Hastie, R. Tibshirani, and J. Taylor. An Introduction to Statistical Learning: With Applications in Python. Springer Nature, Cham, Switzerland, June 2023.
- W. Jiang and Z. A. Pardos. Evaluating sources of course information and models of representation on a variety of institutional prediction tasks. International Educational Data Mining Society, 2020.
- V. Karpukhin, B. Oğuz, S. Min, P. Lewis, L. Wu, S. Edunov, D. Chen, and W. tau Yih. Dense passage retrieval for open-domain question answering, 2020.
- M. Kim, A. Puder, C. Hayward, and H. Yang. Foundation models for course equivalency evaluation. In 2024 IEEE International Conference on Data Mining Workshops (ICDMW), pages 300–306, 2024.
- B. Li, H. Zhou, J. He, M. Wang, Y. Yang, and L. Li. On the sentence embeddings from pre-trained language models, 2020.
- Q. Liu, M. J. Kusner, and P. Blunsom. A survey on contextual embeddings, 2020.
- B. Loo. Education in the United States of America, 2018.
- H. Ma, X. Wang, J. Hou, and Y. Lu. Course recommendation based on semantic similarity analysis. In 2017 3rd IEEE International Conference on Control Science and Systems Engineering, pages 638–641, 2017.
- G. McLachan. Discriminant Analysis and Statistical Pattern Recognition. Probability & Mathematical Statistics S. John Wiley & Sons, Nashville, TN, May 1992.
- R. Morsomme and S. V. Alferez. Content-based course recommender system for liberal arts education. In Proceedings of The 12th International Conference on Educational Data Mining, volume 748, page 753, 2019.
- P. Previde, C. Graterol, M. Love, and H. Yang. A data mining approach to understanding curriculum-level factors that help students persist and graduate. In 2019 IEEE Frontiers in Education Conference (FIE), 2019, pages 1–9, 2019.
- Regents of the University of California, The. Fall enrollment at a glance, 2024.
- H. Steck, C. Ekanadham, and N. Kallus. Is cosine-similarity of embeddings really about similarity? In Companion Proceedings of the ACM Web Conference 2024, WWW ’24, page 887–890. ACM, May 2024.
- E. Tang, B. Yang, and X. Song. Understanding llm embeddings for regression, 2025.
- G. V. Trunk. A problem of dimensionality: A simple example. IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-1(3):306–307, 1979.
- Y. Wang, H. Huang, C. Rudin, and Y. Shaposhnik. Understanding how dimension reduction tools work: An empirical approach to deciphering t-sne, umap, trimap, and pacmap for data visualization, 2020.
- H. Yang, T. Olson, and A. Puder. Analyzing computer science students’ performance data to identify impactful curricular changes. In 2021 IEEE Frontiers in Education Conference (FIE), 2021, pages 1–9, 2021.
- H. Yang, A. D. Pimparkar, C. Graterol, R. A. Kased, and M. B. Love. Analyzing college students’ advising records to improve retention and graduation outcome. In 2021 IEEE Frontiers in Education Conference (FIE), pages 1–8, 2021.
- W. X. Zhao, K. Zhou, J. Li, T. Tang, X. Wang, Y. Hou, Y. Min, B. Zhang, J. Zhang, Z. Dong, Y. Du, C. Yang, Y. Chen, Z. Chen, J. Jiang, R. Ren, Y. Li, X. Tang, Z. Liu, P. Liu, J.-Y. Nie, and J.-R. Wen. A survey of large language models, 2025.
© 2025 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.