ABSTRACT
Previous studies suggest that Deep Knowledge Tracing (or DKT) has fundamental limitations that prevent it from supporting mastery learning on multi-step problems [15, 17]. Although DKT is quite accurate at predicting observed correctness in offline knowledge tracing settings, it often generates inconsistent predictions for knowledge components when used online. We believe this issue arises because DKT’s loss function does not evaluate predictions for skills and steps that do not have an observed ground truth value. To address this problem and enable DKT to better support online knowledge tracing, we propose the use of a novel loss function for training DKT. In addition to evaluating predictions that have ground truth observations, our new loss function also evaluates predictions for skills that do not have observations by using the ground truth label from the next observation of correctness for that skill. This approach ensures the model makes more consistent predictions for steps without observations, which are exactly the predictions that are needed to support mastery learning. We evaluated a DKT model that was trained using this updated loss by visualizing its predictions for a sample student learning sequence. Our analysis shows that the modified loss function produced improvements in the consistency of DKT model’s predictions.
Keywords
1. INTRODUCTION
Intelligent tutoring systems are widely used in K-12 education and online learning platforms to enhance learning. Knowledge tracing algorithms are embedded in such intelligent tutoring systems to support automatic selection of the problems a learner should work on next based on their mastery of different skills. There are multiple popular knowledge tracing algorithms that are frequently used to predict students’ performance in offline settings. While these approaches have all achieved satisfactory performance in these settings, there is only limited work investigating the use of knowledge tracing algorithms in online settings [11, 17].
Deep Knowledge Tracing (DKT) is a knowledge tracing approach that has gained in popularity in recent years. It employs a recurrent neural netwok (RNN) [16] to predict student’s correctness on problem-solving steps that use particular skills. Though some studies demonstrated that DKT outperforms other knowledge tracing models such as Bayesian Knowledge Tracing [1] and Performance Factors Analysis (PFA) [10], it has some fundamental limitations and drawbacks. For example, DKT’s neural network representation is not easily interpretable, making it difficult for people to understand DKT’s predictions. Additionally, Yeung and Yeung [15] identified two problems with DKT—the model fails to reconstruct the observed input, and the DKT predictions are inconsistent and fluctuate over time.
In this paper, we investigate the issue of inconsistent predictions. Our work explores the hypothesis that DKT’s inconsistent behavior is primarily due to its loss function. We propose a novel modification to the DKT loss functions designed to produce more consistent behavior. Multiple authors have proposed ways of modifying the loss function by adding regularization terms [7, 8, 15]. However, our research explores a novel modification that evaluates predictions for each skill that does not have an observed ground truth value by using the next observed correctness for that skill.
We use the “Fraction Addition and Multiplication, Blocked vs. Interleaved” dataset accessed via DataShop [5] to evaluate a DKT model generated through training with this new loss function by visualizing its predicted correctness for each skill at each time step in a heatmap. We then compare these results with the predictions generated by a DKT model trained using the original loss function. Our results indicate that training with the revised loss function produces a DKT model that generates more consistent predictions than one produced by training with the original loss function.
2. BACKGROUND
2.1 Knowledge Tracing
Knowledge tracing approaches model a student’s knowledge over time and predict their performance on future problem-solving steps. Knowledge tracing algorithms are embedded in Intelligent Tutoring Systems to support automatic selection of the next problem a student will practice [13]. Much of the research on knowledge tracing has explored its use in offline settings; however, little work has explored the use of knowledge tracing in online settings. In offline settings, knowledge tracing models are fit to existing data sets, typically to evaluate different knowledge component models to identify those that better fit the data. In contrast, the objective of online knowledge tracing is to keep track of the student’s level of mastery for each skill (or knowledge component) and/or predict the student’s future performance based on their past activity. In a nutshell, knowledge tracing seeks to observe, depict, and quantify a student’s knowledge state, such as the level of mastery of skills underlying the educational materials [6]. The outputs of knowledge tracing support mastery learning and intelligent selection of which problems a student should work on next.
2.2 Deep Knowledge Tracing
Pieche et al. [12] proposed the Deep Knowledge Tracing (DKT) approach, makes use of a Long Short-Term Memory (LSTM) [4] architecture (complex variant of Recurrent Neural Network, or RNN) to represent latent knowledge. The use of an LSTM has become increasingly popular because it reduces the effect of vanishing gradients. It employs cell states and three gates to determine how much information to remember from previous time-steps and also how to combine that memory with information from the current time-step.
The DKT model accept an input matrix , which is constructed by one-hot encoding two pieces of information for each step: , which represents the knowledge components, and , which represents whether the question was answered correctly. The information at each time step is packed into a tuple denoted as . represent the initial state at time 0 (where t = 0). The network outputs the prediction based on the input and previous state. is a matrix that represents the probability of each KC being correctly answered at each step by a given student. is the predicted probability at time .
The objective of DKT is to predict performance at the next iteration (given the data from time to , predict ). To optimize next iteration results, a dot product of the output vector and the one-hot encoded vector of the next practiced KC is calculated. We take the cross entropy (denoted as ) of the dot product, average over number of steps and number of students. All together, the original loss function of DKT can be expressed as:
(1)where is the number of students, and is the length of the interaction sequence for student .
When the size of a dataset increases, deep knowledge tracing generally has an edge over the classical statistical models, such as Bayesian Knowledge Tracing, Streak Model or Performance Factor Analysis, when it comes to predicting learner performance. The original DKT work [12] demonstrated that it can produce tremendous gains in AUC (e.g., 25%) when compared to prior results obtained from other knowledge tracing models. However, subsequent work suggests that the gains are not as large as originally anticipated [14]. One of the key advantages of DKT over classical knowledge tracing methods, such as BKT, is that it has access to more precise information about the temporal order of interactions as well as information about KCs not involved in the current step [2]. We intend to leverage these advantages of DKT to support online knowledge tracing [17] and explore whether it is possible to get better mastery learning behavior when using DKT rather than classical knowledge tracing approaches, such as BKT.
2.3 Challenges with DKT
Even though DKT has many advantages over other knowledge tracing models like Bayesian Knowledge Tracing (BKT) [1], Streak Model [3] and Performance Factor Analysis (PFA) [10], the model still has several limitations. Specifically, DKT models are difficult to interpret [14], make inconsistent predictions [15], and only consider the correctness of skills that are observed on each time step [7].

Yeung and Yeung [15] identified that the DKT predictions are not consistent and fluctuate over time. They also showed that the DKT model fails to reconstruct the input information in its predictions. For example, DKT may predict lower correctness on steps tagged with a particular skill even when the student correctly performs steps that contain the skill. Figure 1 is an example of this effect. From the first to the third steps, the student did not answer the problem correctly, but DKT predicted the third step would have a 100% chance of being correct. From the fourth to the sixth steps, the student correctly answered the question while DKT’s predictions dropped. Upon closer investigation of the DKT model, we believe that this unexpected behavior is due to the way that the loss is computed.
Our previous work [17] highlighted DKT’s shortcoming with respect of giving reliable predictions of correctness on steps tagged with each skill during online knowledge tracing. We want to further investigate the issues that prevent DKT from giving consistent predictions in the scenario of multi-step problem solving and online knowledge tracing. In this paper, we propose a novel revision of DKT’s loss function. We will discuss our approach in Section 3.1.
3. METHODOLOGY
We propose a novel approach to make the DKT model predictions more consistent by modifying the loss function used during training. We trained and tested on the “Fraction Addition and Multiplication, Blocked vs. Interleaved” dataset accessed via DataShop [5] with 80% training data and 20% testing data. This data was collected from a study presented in [9], the students solved problems by interacting with a fraction arithmetic tutor and solved three different types of problems. The three problem types are: Add Different (AD), add fractions with different denominators; Add Same (AS), add fractions with same denominators; Multiplication (M), multiply two fractions.
We created two DKT models: one trained using the original DKT loss function and another trained using the modified loss function. We then used the two models to make predictions on the same student sequence. Lastly, we visualized the predictions for each knowledge component (KC) as heat maps and evaluated the prediction consistency by comparing the heat maps generated using the different DKT models.
All DKT models in this paper consists of a input layer, a hidden layer, and a output layer with size 28, 200, and 14, respectively. The number of knowledge components determines the size of the input and output layers. The LSTM (long short-term memory) contained 200 hidden units. We trained the model over 1000 epochs, with a learning rate of 0.0025, a dropout rate of 0.4, and a batch size of 5. The only difference between the original DKT approach and our approach is the loss function used during training.
3.1 Revision of DKT Loss Function
As outlined in Section 2.3, DKT’s original loss function only evaluates the DKT predictions that have observed ground truth values. To overcome this challenge, we propose a revision to the loss function. Rather than using the original ground truth values typically provided to DKT’s loss function, our revised approach uses modified ground truth data that fills in steps without any observations by taking the next observation of that skill (see Figure 2).
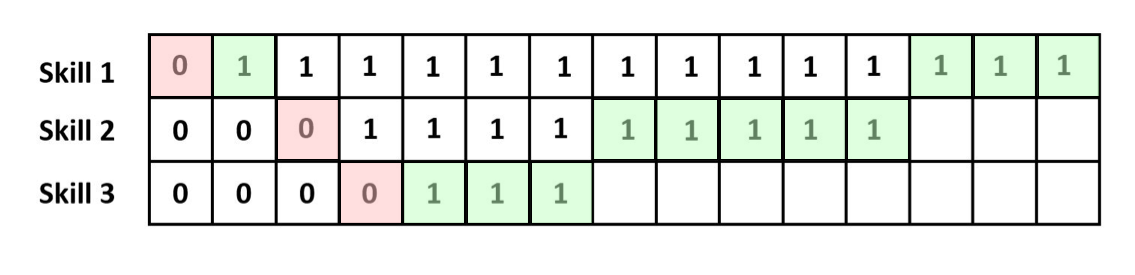
Mathematically, we use to represent the updated ground truth values that populate missing cells using the value from the next observation of each skill, see Figure 2. For example, for a specific knowledge component, if there is no ground truth at and the next ground truth is at , then the contains an entry at that has the same value as the entry at . As a result, the entries from to would share the same ground truth with .


Next, we updated the loss function so that it evaluates the model’s predictions for all entries that have a value in the updated ground truth values (). Here is the mathematical representation of this new loss function:
(2)This updated loss function will evaluate most of the DKT predictions that did not originally have observed ground truth values. Note, some predictions are still not evaluated (those that occur near the end and do not have a next observation to use for evaluation). Because this new loss function evaluates more of DKT’s predictions in between observations, we believe it will result in more stable predictions.
4. MODEL EVALUATION
To evaluate the performance of DKT model after revising the loss function, we took a complete student sequence and generated correctness predictions for each skill using the DKT model. We have 14 skills (knowledge components) and three types of problems as introduced in Section 3. There are 8 steps for an Add Different (AD) problem, 3 steps for an Add Same (AS) problem, and 3 steps for a Multiplication (M) problem. Figure 3 is a comparison of the student’s predicted mastery of each KC at each step when solving a problem (problem type shown on the x-axis). We use the color to represent DKT’s prediction, with green indicating the student mastering a skill and red indicating not mastering a skill. We use the numbers to represent the ground truth where 1 equals correct and 0 equals incorrect. Figure 2b shows a substantial improvement in prediction consistency over Figure 2a.
In Figure 2a, the DKT predictions fluctuate over time. There is also a pattern of inconsistent predictions on the “AD Right Convert Numerator”, “AD Answer Numerator” and “AD Done” skill even though the ground truth values for these skills are 1 during the series of problems practiced. Initially, the DKT model trained using the original loss predicts that the student masters this skill after a few practices. However, we see that for certain repeating periods over the remainder of the sequence, the model predicts the student will get steps with these skills wrong. The student mastered these three skills initially. As the student starts solving additional steps, however, the DKT model alternates between correct and incorrect predictions over the remainder of the sequence. These behaviors are unexpected and contrary to the typical assumption that students will not forget skills once they obtain mastery.
In Figure 2b, the problem of wavy DKT predictions (alternating correct and incorrect predictions for different skills) is largely addressed. The DKT model with the revised loss predicts that the student obtains mastery on all the AD skills and retains this mastery through the end of training. The DKT predictions are consistent with the ground truth in this case.
These results suggest that our revised loss function produces more consistent DKT model predictions. Besides the improvement, we noticed a common issue that occurred in both the original and the revised DKT model. The student started with 10 AS problems but both DKT models predict improvement of mastery in M and AD skills even before M and AD problems were given to the student. We believe that more work is needed to better understand how DKT relates the corresponding skills in a multi-step problem.
5. RELATED WORKS
Multiple authors have discussed the limitations of DKT in handling multi-skill sequences and possible modifications to the loss function to improve model behavior. Yeung and Yeung [15] proposed regularization terms to address the reconstruction problem (where model predictions move opposite to student performance) and the wavy prediction transition problem (where skill predictions cycle between high and low). Inspired by their study, we believe that revising the loss function is the key to enhancing the consistency of DKT model predictions. Rather than addressing these two problems separately using regularization terms, our approach modifies the loss function so that it evaluates predictions that lack ground truth observations.
Beyond modifying the loss function, Pan and Tezuka [8] proposed pre-training regularization, which incorporates prior knowledge by including synthetic sequences to the neural network before training DKT with real student data. Their motivation is similar to ours—their goal is also to solve the inverted prediction problem (referred to as the reconstruction problem by Yeung and Yeung). They added synthetic data to a baseline model trained with student data and then introduced two regularization measures to measure the severity of the inverted prediction problem. This approach is different from ours as we are using the ground truth value of each skill to populate skills and steps that do not have observations.
6. CONCLUSIONS AND FUTURE WORK
We revised DKT’s loss function to improve prediction consistency across all KCs over time. Our main contribution is that we propose a novel way of modifying the DKT loss function by evaluating skill predictions at the time steps that lack ground truth observations. Instead of only addressing DKT’s consistency issues, our ultimate goal is to use DKT as an approach to keep track of student performance in online learning environments and recommend problems to support personalized learning.
Through our heat map analysis, we demonstrated that a DKT model trained with our improved loss function generates more consistent predictions than a DKT model trained with the original loss. Our analysis showed that predictions for certain skills would cycle between high and low for a DKT model trained with the original loss function; i.e., generated inconsistent predictions over time. In contrast, the DKT model trained with the revised loss function showed much smoother, more consistent predictions that started lower and improved steadily over the course of training.
Moving forward, we have a number of additional future directions that we would like to explore to improve DKT’s stability and accuracy. In our current work, we propose an updated loss function that evaluates the DKT predictions for each skill in terms of the next observation of that skill. In future work, we instead want to evaluate each prediction in terms of all future predictions. Further, we plan to weight each evaluation by a decay factor as Yeung & Yeung [15] proposed in their future direction. Finally, we should move online and evaluate how well the revised DKT operates in an online mastery learning context.
7. ACKNOWLEDGMENTS
This work was funded by NSF award #2112532. The views, opinions, and/or findings expressed are those of the authors and should not be interpreted as representing the official view or policies of the funding agency.
8. REFERENCES
- A. T. Corbett and J. R. Anderson. Knowledge tracing: Modeling the acquisition of procedural knowledge. User modeling and user-adapted interaction, 4(4):253–278, 1994.
- T. Gervet, K. Koedinger, J. Schneider, T. Mitchell, et al. When is deep learning the best approach to knowledge tracing? Journal of Educational Data Mining, 12(3):31–54, 2020.
- N. T. Heffernan and C. L. Heffernan. The assistments ecosystem: Building a platform that brings scientists and teachers together for minimally invasive research on human learning and teaching. International Journal of Artificial Intelligence in Education, 24(4):470–497, 2014.
- S. Hochreiter and J. Schmidhuber. Long short-term memory. Neural computation, 9(8):1735–1780, 1997.
- K. R. Koedinger, R. S. Baker, K. Cunningham, A. Skogsholm, B. Leber, and J. Stamper. A data repository for the edm community: The pslc datashop. Handbook of educational data mining, 43:43–56, 2010.
- Q. Liu, S. Shen, Z. Huang, E. Chen, and Y. Zheng. A survey of knowledge tracing. arXiv preprint arXiv:2105.15106, 2021.
- Q. Pan and T. Tezuka. Accuracy-aware deep knowledge tracing with knowledge state vector loss. pages 90–92, 2020.
- Q. Pan and T. Tezuka. Prior knowledge on the dynamics of skill acquisition improves deep knowledge tracing. In Proceedings of the 29th International Conference on Computers in Education, pages 201–211, 2021.
- R. Patel, R. Liu, and K. R. Koedinger. When to block versus interleave practice? evidence against teaching fraction addition before fraction multiplication. In Proceedings of Cognitive Science Conference, pages 2069–2074, 2016.
- P. I. Pavlik, H. Cen, and K. R. Koedinger. Performance factors analysis–a new alternative to knowledge tracing. In Proceedings of the 2009 conference on Artificial Intelligence in Education: Building Learning Systems that Care: From Knowledge Representation to Affective Modelling, pages 531–538, 2009.
- R. Pelánek. Bayesian knowledge tracing, logistic models, and beyond: an overview of learner modeling techniques. User Modeling and User-Adapted Interaction, 27(3):313–350, 2017.
- C. Piech, J. Bassen, J. Huang, S. Ganguli, M. Sahami, L. J. Guibas, and J. Sohl-Dickstein. Deep knowledge tracing. In C. Cortes, N. Lawrence, D. Lee, M. Sugiyama, and R. Garnett, editors, Advances in Neural Information Processing Systems, volume 28. Curran Associates, Inc., 2015.
- J. Rollinson and E. Brunskill. From predictive models to instructional policies. Proceedings of the 8th International Conference on Educational Data Mining, EDM 2015, pages 179–186, 2015.
- X. Xiong, S. Zhao, E. G. Van Inwegen, and J. E. Beck. Going deeper with deep knowledge tracing. International Educational Data Mining Society, 2016.
- C.-K. Yeung and D.-Y. Yeung. Addressing two problems in deep knowledge tracing via prediction-consistent regularization. In Proceedings of the Fifth Annual ACM Conference on Learning at Scale, pages 1–10, 2018.
- W. Zaremba, I. Sutskever, and O. Vinyals. Recurrent neural network regularization. arXiv preprint arXiv:1409.2329, 2014.
- Q. Zhang and C. J. Maclellan. Going online: A simulated student approach for evaluating knowledge tracing in the context of mastery learning. International Educational Data Mining Society, 2021.
© 2022 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.