A deep reinforcement learning approach to automatic formative feedback
Aubrey Condor
University of California Berkeley
aubrey_condor@berkeley.edu
Zachary Pardos
University of California Berkeley
pardos@berkeley.edu

ABSTRACT

Receiving formative feedback about open-ended responses can facilitate the progression of learning. However, educators cannot often provide immediate feedback and thus for students, learning may be slowed. In this paper, we will explore how an automatic grading model can be coupled with deep Reinforcement Learning (RL) to create a system of automatic formative feedback on students’ open-ended responses. We use batch (offline) learning with a double Deep Q Network (DQN) to simulate a learning environment, such as an open-source, online tutoring system, where students are prompted to answer open-ended questions. An auto-grader is used to provide a rating of the student’s response, and until the response is scored at the highest category, an RL agent iteratively provides suggestions to the student to revise the previous version of their answer. The automated suggestion can include either a key idea to consider adding to the response, or a recommendation to delete a specific part of the response. Our experiments are based on a simulated environment, within which we anticipate a how a real student might revise their answer based on the agent’s chosen hint. Preliminary results show that in such environment, the agent is able to learn the best suggestions to provide a student in order to improve the student’s response in the least number of revisions.

Keywords

Formative Feedback, Deep Reinforcement Learning, Automatic Short Answer Grading

1. INTRODUCTION

It has been shown that the use of open-ended (OE) items is beneficial for student learning by self-explanation [2], or information recall [1]. Additionally, receiving formative feedback – information communicated to the learner intended to modify his or her thinking/behavior to improve learning - about OE responses may also contribute to the progression of learning for students [16]. However, assessing OE items and subsequently providing formative feedback is time consuming for teachers [6] and consequently, feedback to students can be delayed.

We suggest the use of educational technology to help mitigate this issue. Technologies like online learning platforms or intelligent tutoring systems can enable students to take a proactive role in assessing their own abilities. In addition, they can help promote equitable learning for students who do not have the resources to receive quick and individualized feedback from a human tutor, parent, or private educator. Such platforms have the capability to provide instant feedback, allowing for students, of all types, to take control of their own learning through real-time formative self-assessment [11]. However, items that elicit instant feedback necessitate a structure for automatic grading, and the creation of useful feedback. While implementing automatic grading and producing related feedback for multiple choice items is seamless, as a student’s response is limited to a small number of choices, it is not so simple for OE questions that elicit an infinite number of potential student responses.

In this paper, we explore how an Automatic Short Answer Grading (ASAG) model can be coupled with deep Reinforcement Learning (RL) to create a system that provides automatic formative feedback for students’ OE responses. We will use batch (offline) learning to simulate an environment, such as an open source tutoring system, where students are prompted to answer OE questions. Once the ASAG model provides a rating of the response, the RL agent will give a hint to the user by suggesting either a key phrase that the user might consider adding to the response, or a portion of the response that the user might want to delete when revising their answer. The student’s revision will be simulated by either the key phrase being added to the previous response at the agent’s chosen index within the response, or the portion to consider removing deleted completely. The new response will be once again sent to the auto grader to be classified. This process will continue until the automated rating has reached some defined threshold (as a function of the reward), or a maximum number of hints has been provided.

The key idea of our work is to train an RL agent to choose the best sequence of revisions for an OE response, in order to arrive at an exemplary response in the least number of revisions. Although the space of student responses to a given question is infinite, we hypothesize that the agent can learn which of a finite set of revisions will be most useful to improve a student’s answer.

The main contribution of this work is to explore a real-world application of deep RL. There has been little work so far studying the use of deep RL in educational contexts, and in addition, coupling deep RL with language models (the auto grader) has not been extensively investigated. In this paper, we will briefly describe the ASAG, but will mainly focus on the implementation of the deep RL algorithm.

2. RELATED WORK

Several works have focused on the use of RL for applications in education. Reddy et. al (2017) created a model-free review scheduling algorithm to learn a policy that operates on raw observations of a student’s study history, as opposed to explicitly modeling the student as employed by other scheduling algorithms [13]. Iglesias et. al (2009) used RL within a pedagogical module of an education system such that the system would automatically learn which pedagogical policy was best for a particular student [7]. Dorça et. al (2013) presented an automatic probabilistic approach for modeling student’s learning styles based on reinforcement learning [5]. They show that because of the dynamic aspects of detecting learning styles, the RL agent is able to constantly adjust to a student’s performance. Park et. al (2019) introduced an RL “social robot” for personalized and adaptive education [12]. They illustrate how the agent can utilize children’s verbal and nonverbal affective cues to exert influence over the student’s engagement, in order to maximize long-term learning gains. Rowe et. al (2015) employ modular RL, a multi-goal extension of classic RL, to dynamically tailor narrative-centered learning to particular students’ needs [14]. They show that including a data-driven, planning approach can enhance student learning. Finally, Shawky & Badawi (2018) use RL to build an intelligent environment that provides a method to account for the continuously-changing states of student learners [15].

3. BACKGROUND

In this section we will provide a brief overview of the methods used in our work necessary to understand the results, including the ASAG model, offline (batch) learning, Q-learning and Epsilon-greedy sampling.

3.1 Deep Reinforcement Learning

Reinforcement learning (RL) employs learning to control a dynamical system by providing feedback to an agent, via a reward system, in order to choose an action to take in a given state. The action consists of what the agent can do in the state, where the state represents the current condition of the agent. When the agent takes an action, it receives a reward (either positive or negative) as feedback from the environment. Thus, the agent learns a policy to maximize its total expected sum of rewards. The system can be defined as a fully or partially-observed Markov decision process (MDP) [17].

Deep RL utilizes high-capacity function approximators - deep neural networks - as the policy, in conjunction with RL. The incorporation of deep networks has improved performance for applications of RL in many domains [8]. With deep RL, the agent can make decisions from unstructured data without any manual engineering of the state space and the algorithms can handle very large amounts of data for learning an optimal policy.

3.2 The ASAG model

The Automatic Short Answer Grading (ASAG) model that we use to provide an initial rating of student responses, as well as feedback to the agent through a reward function about the chosen action (response revision), is a BERT-base multi-class classification model. The BERT transformer language model, introduced in [4], is pre-trained on large amounts of natural language text from Wikipedia and BooksCorpus, and can be fine-tuned for downstream tasks such as classification. We use a compressed version of the model called BERT-base, and fine-tune the model as a supervised classifier using human ratings of the OE question(s) as ground-truth ratings.

3.3 Offline (batch) learning

Traditionally, RL algorithms employ online learning by iteratively collecting experiences, i.e. data, while actively interacting with the environment. The collected experiences are used by the model to improve the policy [17]. For some applications, however, using online data collection can be resource heavy or dangerous or impractical for settings that necessitate a large dataset [8]. In contrast, offline RL algorithms utilize previously collected data. Data is stored in a replay buffer and is not altered during training, allowing for the incorporation of very large, or pre-existing datasets. Issues posed by fully offline-learning algorithms include, most prominently, a vulnerability to distributional shift.

3.4 Deep Q Learning

Q-learning is categorized as a model-free reinforcement learning algorithm - i.e. it does not use the transition probability distribution or the reward function associated with the MDP. Essentially, the model-free algorithm is based on trial-and-error. For any finite MDP, the Q-learning algorithm will find an optimal policy that maximizes the expected total reward over all steps in the sequence, starting from the current state [9]. The Q-function determines the value of a state-action pair through the given reward. Deep Q-learning is a variant of Q-learning where a nonlinear function approximator - a neural network - represents Q.

4. TRAINING THE RL AGENT

In this section, we describe the dataset used for initial results as well as the RL formulation consisting of the state, reward, and action set.

4.1 The Dataset

To evaluate our proposed methods, we take the most simple approach and use only one OE science question from an open-source data set called the Automatic Student Assessment Prize, Short Answer Scoring data (ASAP-SAS). The data was used in a 2012 Kaggle competition1 sponsored by the Hewlett Foundation, and consists of almost 13,000 short answer responses to 10 science and English questions. The questions were scored from 0 (most incorrect) to 3 (most correct), and each question includes a scoring rubric. We chose the question that achieved the highest validation accuracy, evaluated with a Cohen’s Kappa Metric, with the automatic grading model. We did so such that the reward signal, as it is a function of the autograder, would be strong and consistent, rather than using a question that the autograder has a difficult time scoring and may subsequently provide inconsistent reward feedback to the agent.

The question prompt asks students to "List and describe three processes used by cells to control the movement of substances across the cell membrane." And the rubric states that an answer rated at the highest level will include three correct processes, down to the lowest level which will include zero correct processes. Examples of key statements that can/should be included in an answer, according to the rubric, include: "Selective permeability is used by the cell membrane to allow certain substances to move across", or "Osmosis is the diffusion of water across the cell membrane". The list of key statements include in the rubric drove the action space selection of phrases that the RL agent can add to a response (to simulate suggesting that a student consider the information in their revision).

4.2 The Algorithm

An overview of the proposed algorithm is as follows. For each episode, we will first initialize by randomly sampling one of the student’s short answers. The student answer text will be vectorized and fed to the agent. Based on this state input, the agent will choose an action to take, i.e., either adding a key phrase or deleting a portion of the response. This simulates the student taking the hint into account when revising their answer. Next, we send the new student response to our language model classifier, and receive a probability distribution of rating categories as output. Then we will calculate our reward as a function of the difference in class probabilities from the previous response, to the newly revised response, such that an increased probability of the highest rating category for the revised response would correspond to a higher reward. If the response has reached a high rating, the episode will terminate. Otherwise, the process is repeated with the revised student response (the original response plus the hint phrase, or minus the deleted portion) as the new state, and the agent will choose another action until the highest rating is achieved, or we reach a pre-defined maximum number of revisions. Details of the process are described below.

4.2.1 The State

The state is primarily represented by a student’s response. As our RL agent will not take in words as input, we vectorize the student responses using a Word2Vec [10] model, with embeddings of size 8, and a vocabulary specific to our dataset. Word2Vec produces an embedding for each word in the vocabulary, so in order to create one embedding for the entire response, we concatenate the individual word embeddings. W2V mbeddings of size 8 are particularly small, but we chose to sacrifice some information within the word embeddings in order to keep our state space at a reasonable size. Additionally, we concatenate each word embedding instead of averaging them, which is a common method for producing sentence embeddings because we want the agent to have a capacity to interpret the response at the word level, and not only as an aggregate response.

4.2.2 The Reward

The reward is a function of the difference in the ASAG model’s classification probability distribution of ratings between the old response and the revised response, with a penalty for each revision the agent makes. We include the penalty (subtracting 1) because we want the agent to learn how to revise the student’s response in the least number of revision steps. Additionally, we more heavily weighted the higher rating category probability changes because we care more about a change in the highest rating probabilities, as it is the ultimate goal to achieve the highest level rating. Finally, we multiply the weighted difference in probabilities by three, because the overall difference tended to be small, and we needed to send a stronger signal to the agent. The Reward formula is as such, where Δp0 represents the difference in probability of the 0 rating category between the new and old response:

3 ⋅ (0 ⋅Δp0 + 1 ⋅Δp1 + 2 ⋅Δp2 + 3 ⋅Δp3) − 1

4.2.3 The Action Space

The action space consists of both adding key phrases to the response or deleting a portion of the response. The agent can choose only one revision (one addition, or one deletion) in each step. The key phrases the agent can add must be pre-defined by either a subject-matter-expert or created based on a detailed scoring rubric, in order to determine what is necessary for a student to include in their explanation to achieve a high rating. For the question in our initial experiment, "List and describe three processes used by cells to control the movement of substances across the cell membrane.", the list of 10 key phrases that the agent can choose from are shown below.

[’energy to move’], [’across cell membrane’], [’diffusion substance across’], [’active transport requires’], [’osmosis water across’], [’passive transport requires’], [’no energy move’], [’from high concentration’], [’to low concentration’], [’with concentration gradient’]

The phrases are vectorized with Word2Vec the same way the response is for the state space. The phrase can be added to the response at any index in increments of 3 (i.e., the phrase can be added to the very beginning of the response at index 0, or three words in at index 3, etc.). We hypothesized that it is necessary that the agent chooses where, within the response, the phrase will be added. Additionally, the action space includes removing any one trigram within the response. We limited the flexibility of the agent removing text to trigrams to keep the action space at a reasonable size. With a larger action space, it is reasonable to assume that the agent will take much longer to learn.

4.2.4 The Q Network

The Q-Network consists of a fully connected neural network with two hidden layers of size 300 and 200. The final layer corresponds to the dimension of the action space. In addition, both hidden layers use an Rectified Linear Unit (ReLU) activation function. As input, the network takes in the state space (vectorized student response) and outputs an estimate of the expected future sum of rewards of each action in the action space. Thus, the agent chooses the action that has the maximum Q Network output. Our algorithm is optimized using Adam stochastic optimization [3]. The size of the replay buffer for the Q-Network is 10,000. In addition, the Q-Network is trained with a batch size of 32, a discount factor of 0.99, and a learning rate of 5e-4. We update the target network every 4 episodes.

5. RESULTS

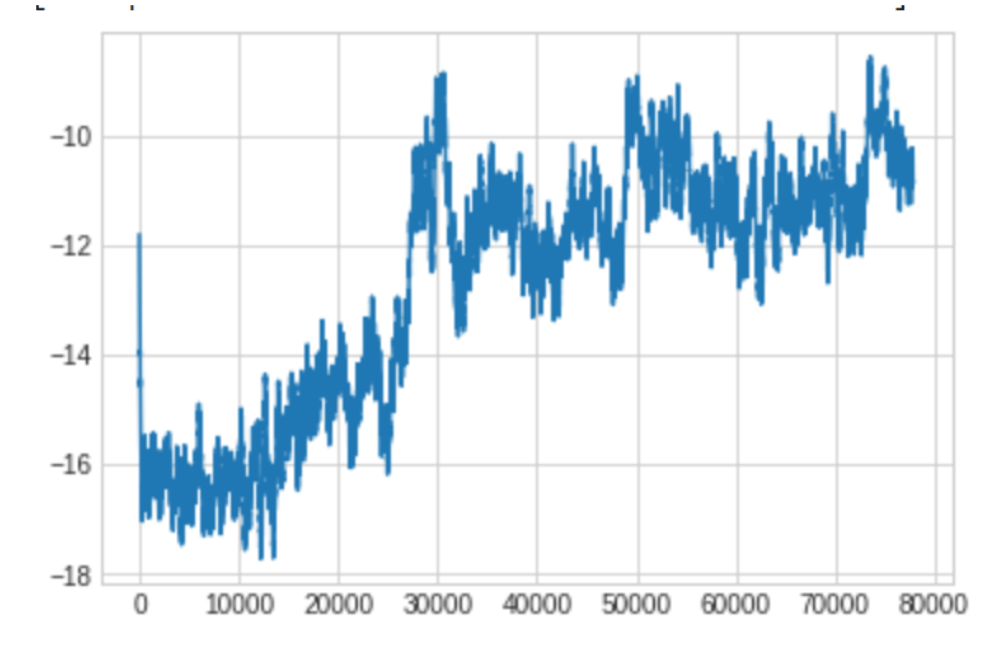
Preliminary results shown in Figure 1 imply that the agent is indeed able to learn which revisions to make to a response in order to achieve a higher rating from the autograding model. Figure 1 shows the sum of rewards in an episode on the y-axis, and the episode number along the x-axis. The scale or number of the y-axis is not necessarily meaningful, as our reward function is only created as a means to give signal to the agent about the goodness of its sequence of decisions. Rather, the overall pattern of the reward becoming less negative, i.e. greater, as the training episodes increase shows us that the agent can learn, over many episodes of trial and error, an optimal policy to choose which actions to take, in order to maximize its future sum of rewards. It is worth noting that with limited computational resources, training the agent over 80,000 episodes is not quick, so future work will indeed include training over a greater number of episodes, to see if the agent can achieve a somewhat convergence to a higher total episodic reward than is shown in Figure 1.

The sum of rewards increases, although not linearly, over 80 thousand training episodes, indicating that the agent has learned.
Figure 1: Sum of rewards over 80K training episodes.

6. DISCUSSION

We emphasize that this project is a work in progress and acknowledge that there is much more effort needed to explore the agent’s capacity to revise a students response. We believe that it is an important and successful first step to observe that the RL agent is indeed able to learn the task that we proposed, as there exist many sequential tasks that may not be appropriate for the RL formulation, or are too complicated for an RL agent to learn. Using a reward that is a function of a language model poses a unique challenge as we adopt the limitations of the autograding model itself into our reward formulation. Additionally, using concatenated word vectors as a state space adds an additional layer of complexity because the variability in the state space is infinite, as any student may use an infinite combination of words in their response.

More importantly, we note that there are several practical application of an RL agent revising a student’s response. Our results are from a simulated environment that is meant to represent a real-life student interaction, but does not do so perfectly. When thinking forward to the real-life application of implementing the algorithm in the context of a real student revising their answer, many unanswered questions arise. Firstly, we assume that a student will take into account the RL agent’s revision suggestion directly in our simulation (the agent automatically adds the key phrase or deletes the segment), but a real student will have the choice to consider the suggestion or ignore it and make a different revision. This may pose confusing signals to the agent about whether or not the suggestion was the best one. Further, we must investigate how exactly to provide the hints, as formative feedback, such that the student actively learns from their revision.

7. REFERENCES

  1. S. Bertsch, B. J. Pesta, R. Wiscott, and M. A. McDaniel. The generation effect: A meta-analytic review. Memory & cognition, 35(2):201–210, 2007.
  2. M. T. Chi, N. De Leeuw, M.-H. Chiu, and C. LaVancher. Eliciting self-explanations improves understanding. Cognitive science, 18(3):439–477, 1994.
  3. K. Da. A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
  4. J. Devlin, M.-W. Chang, K. Lee, and K. Toutanova. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805, 2018.
  5. F. A. Dorça, L. V. Lima, M. A. Fernandes, and C. R. Lopes. Comparing strategies for modeling students learning styles through reinforcement learning in adaptive and intelligent educational systems: An experimental analysis. Expert Systems with Applications, 40(6):2092–2101, 2013.
  6. C. L. Hancock. Implementing the assessment standards for school mathematics: Enhancing mathematics learning with open-ended questions. The Mathematics Teacher, 88(6):496–499, 1995.
  7. A. Iglesias, P. Martínez, R. Aler, and F. Fernández. Learning teaching strategies in an adaptive and intelligent educational system through reinforcement learning. Applied Intelligence, 31(1):89–106, 2009.
  8. S. Levine, A. Kumar, G. Tucker, and J. Fu. Offline reinforcement learning: Tutorial, review, and perspectives on open problems. arXiv preprint arXiv:2005.01643, 2020.
  9. F. S. Melo. Convergence of q-learning: A simple proof. Institute Of Systems and Robotics, Tech. Rep, pages 1–4, 2001.
  10. T. Mikolov, K. Chen, G. Corrado, and J. Dean. Efficient estimation of word representations in vector space. arXiv preprint arXiv:1301.3781, 2013.
  11. D. J. Nicol and D. Macfarlane-Dick. Formative assessment and self-regulated learning: A model and seven principles of good feedback practice. Studies in higher education, 31(2):199–218, 2006.
  12. H. W. Park, I. Grover, S. Spaulding, L. Gomez, and C. Breazeal. A model-free affective reinforcement learning approach to personalization of an autonomous social robot companion for early literacy education. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 33, pages 687–694, 2019.
  13. S. Reddy, S. Levine, and A. Dragan. Accelerating human learning with deep reinforcement learning. In NIPS’17 Workshop: Teaching Machines, Robots, and Humans, pages 5–9, 2017.
  14. J. P. Rowe and J. C. Lester. Improving student problem solving in narrative-centered learning environments: A modular reinforcement learning framework. In International conference on artificial intelligence in education, pages 419–428. Springer, 2015.
  15. D. Shawky and A. Badawi. A reinforcement learning-based adaptive learning system. In International Conference on Advanced Machine Learning Technologies and Applications, pages 221–231. Springer, 2018.
  16. V. J. Shute. Focus on formative feedback. Review of educational research, 78(1):153–189, 2008.
  17. R. S. Sutton and A. G. Barto. Reinforcement learning: An introduction. MIT press, 2018.

1https://www.kaggle.com/c/asap-sas

© 2022 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.