ABSTRACT
Automated Essay Scoring (AES) research efforts primarily focus on feature engineering and the building of machine learning models to attain higher consensus with human graders. In academic grading such as essay scoring, the scores will naturally result in a normal distribution, more commonly referred to as the bell curve. However, the datasets used do not always have such distribution and are often overlooked in most machine learning environments. This paper proposes a Gaussian Multi-Class Synthetic Minority Over-sampling Technique (GMC-SMOTE) for imbalanced datasets. The proposed GMC-SMOTE generates new synthetic data to complement the existing datasets to produce scores that are in a normal distribution. Using several labeled essay sets, some of which already have a substantial agreement between the machine learning model and human graders, learning from normal distribution datasets yields significant improvements. Improvements of 0.038 QWK score (5.8%) over the imbalanced dataset were observed. The experimental result has also shown that naturally occurring distribution in the automated essay scoring domain contributes to the most appropriate training dataset for machine learning purposes.
Keywords
1. INTRODUCTION
In an educational setting, essay compositions are commonly used to evaluate students’ competence in articulation. The task to grade is labourious and is highly biased to the grader, which causes the scoring to lack consistency in the essay scoring process [20]. For this reason, Automated Essay Scoring (AES) systems have been proposed and implemented to solve the traditional human scoring approach problem or act as a complementary mechanism. Research projects in AES have focused on feature engineering, and in the design of the scoring machine learning models to achieve higher agreement with human graders [19, 22]. In building the machine learning models, the quality of the dataset is of utmost importance. In the earlier research projects on AES, the distribution of the scoring in the datasets was not taken into consideration. The datasets for building the AES models are often imbalanced, as the scores assigned by human graders may not be appropriately distributed. A significant level of imbalance in multi-class datasets such as essay scoring datasets is a profound problem [21].
1.1 Dataset Distribution
To visualise the imbalanced dataset issue in essay scoring, the score distribution of a commonly used dataset for AES research is used. The dataset is from the Automated Student Assessment Prize (ASAP) competition1. There are 8 datasets, where sets 1, 2, 7 and 8 are essays of the same genres were chosen and their score distribution is shown in Figure 1, the other sets are not selected as they are of the short letters genre.
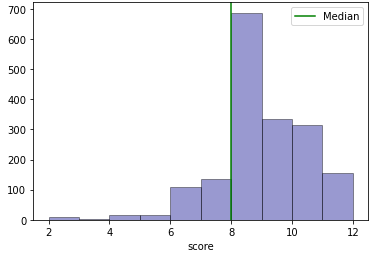
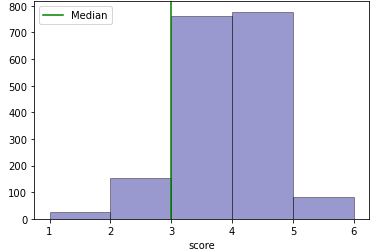
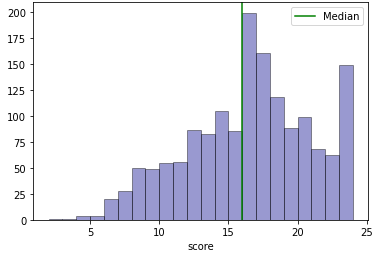
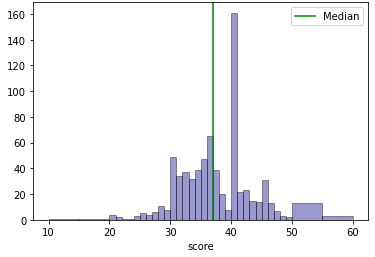
Figure 1a and 1b have fewer classes compared to 1c and 1d. The agreement (accuracy) between the model and the ground truth in a multi-class classifier would generally be better with smaller classes. However, for Essay Set 7 (Figure 1c), the model built for it outperforms that of the smaller number of classes Essay Set 2 (Figure 1b) as shown in Table 0b and 0c. Also, it is observed that Figure 1c has a typical academic scoring distribution that has a Gaussian distribution with a median around the 60% mark. It can also be observed that for Figure 1d, the distribution of the scores does not reflect a Gaussian-like distribution with a trough around the 66% mark. As the scoring range for Figure 1d is larger (0 to 60), this would mean that the dataset quality is poor as there are insufficient data that will result in poor performance of the model by comparing the QWK score of Table 0d with 0a, 0b and 0c. Hence, an appropriate dataset distribution is important for training a model to have better performance.
In automated essay scoring, it is well known that the scoring of academic work such as essays normally falls within a Gaussian distribution curve with the median hovering around the 60 - 70 percentile. Motivated by the understanding that quality training dataset will improve the learned model [10, 3], we propose Gaussian distribution Multi-Class Synthetic Minority Oversampling Technique (GMC-SMOTE) to overcome the issues of imbalanced multi-class data for AES modelling. Instead of implementing SMOTE to provide a uniform distribution of the sampling, GMC-SMOTE is used to oversample the multi-class dataset into a Gaussian distribution. With the improved quality of the training set, the inherent bias of the dataset is kept in the training of the models. To evaluate GMC-SMOTE effectiveness, three type of train sets were generated. In addition, the evaluation was conducted using the same features and modelling algorithm, namely the Bayesian Linear Ridge Regression as proposed by Phandi et al. [19].
2. IMBALANCED DATASET HANDLING
2.1 Imbalanced Data Problem Trends
Researchers worked on the imbalanced data problem from two distinctive approaches; modifications on the attributes at the algorithmic level for the training model to fit the imbalanced data, or augmentation at the data level. These two approaches are summarised as follows.
2.1.1 Algorithmic level
Most of the imbalanced data solutions are targeted on the minority class due to the common high cost of misclassifications on a minority class [18]. Hence, numerous cost-sensitive learning approaches are introduced to balance the classes based on the ratio to each classes’ costs [17]. The most popular approach of cost-sensitive learning is to assign different weights for each class in the training models that are based on the costs of misclassifications [8]. Other than assigning weights, cost-sensitive learning can be done differently, such as changing the models’ threshold based on its own misclassification costs [8]. However, in most real-world cases, the cost matrix is not easily identified.
2.1.2 Data level
Random undersampling (RU) and oversampling (RO) are the first few methods introduced to deal with imbalanced data. Both of the methods replicate random samples to reduce the imbalance ratio. However, the RU might eliminate some significant samples, and RO might cause the model to overfit. There are several extensions based on random undersampling and oversampling such as one-sided selection [15] and Edited Nearest Neighbour rule (ENN) [25]. Synthetic Minority Oversampling Technique (SMOTE) was introduced by Chawla et al. [6] to address the problem in random oversampling. Instead of randomly replicating the minority samples, SMOTE creates new minority class samples by using the interpolation between minority class samples’ neighbourhood. Several extension and hybrid methods based on SMOTE were introduced such as Borderline-SMOTE, SMOTE with Tomek-links and SMOTE with ENN. Eventually, many extensions of SMOTE are proposed such as Borderline-SMOTE [11], ADASYN [13] and MWMOTE [2].
2.2 SMOTE and Multi-Class SMOTE variations
2.2.1 SMOTE
The SMOTE algorithm [6] records the interpolations between minority class instances within a defined neighbourhood to create new synthetic samples. To do so, SMOTE measures the difference between the selected feature vector and its nearest neighbour. SMOTE multiplies the calculated difference by a random number between 0 and 1, then adds it to the selected feature vector. For this reason, the synthetic sample will be at a random point between two specific feature vectors. This method effectively forces the decision making areas for minority class instances to become more generic. However, SMOTE cannot be applied to multi-class problems (such as for AES modeling) directly as SMOTE works on dataset with two classes, the minority, and the majority only. For multi-class problems, there are a few notable multi-class oversampling approaches.
2.2.2 One-versus-All with SMOTE
As multi-class classification implies additional complexity to data mining algorithms, due to the overlapping boundaries, it will lead to a drop in the resulting performance [5]. One of the approaches to tackle this problem is through implementation of class binarization techniques [1]. One-versus-All (OvA), also known as One-versus-Rest (OvR), is a binary classification algorithm for multi-class datasets. The combination of OvA and SMOTE is one of the most popular methods to implement SMOTE for multi-class datasets [10, 3]. OvA is implemented to split the multi-class dataset into multiple binary classification problems. Next, each binary classification problem are trained on a binary classifier based on the samples of selected class as positive and the rest of samples as negative [4]. After obtaining the binary class problems sets from OvA/OvR, SMOTE is implemented for each set to oversample the minority class instances. The output of SMOTE will be merged back into the multi-class dataset for the training of the selected model.
2.2.3 One-versus-One + SMOTE
One-versus-one (OvO) [12] is another approach of binary classification algorithms for multi-class datasets. Similar to OvA/OvR, OvO binarizes multi-class datasets by splitting a multi-class dataset into binary classification problems [9]. However, OvO deals with the datasets differs in that it splits them into single datasets for each class against every other class.
3. PROPOSED GMC-SMOTE
We propose Gaussian Multi-Class Synthetic Minority Oversampling Technique (GMC-SMOTE) to enhance the quality of the dataset in AES by introducing new synthetic samples for improved performance of the models. Instead of creating synthetic new samples uniformly, GMC-SMOTE individually processes each class to form a Gaussian-like distribution. The implementation of SMOTE in a multi-class dataset is not directly applicable. To implement SMOTE in a multi-class dataset, we selected OvA with SMOTE to perform the SMOTE for each class in the multi-class dataset as it has the superior performance over oversampling for multi-class dataset [10, 3]. It is one of the techniques suggested for multi-class oversampling by the author of SMOTE [9].
The default SMOTE algorithm requires six samples for each class, which can be reduced to two. In our proposed GMC-SMOTE algorithm, we propose to replicate classes with fewer than six samples to at least six samples. This ensures SMOTE has sufficient samples to generate synthetic samples and inherit the bias from the original dataset. Also, six samples per class are the minimum requirement to train a model [14].
3.1 GMC-SMOTE Algorithm
2: = Dataset classes and its counts
3: = Dataset
4: Algorithms:
5:
6:
7: for class in C do
8: if then
9:
10: else
11:
12: if then
13:
14: else
15:
16: end if
17: end if
18: end for
19:
20: return
GMC-SMOTE is implemented based on the bell curve symmetric theory [24] for Gaussian distribution. The bell curves symmetric theory means the distribution is symmetric comparing the left distribution and right distribution from the value at the peak of the curve. Algorithm 1 describes our implementation of the GMC-SMOTE. In line 4-7, C represents unique classes and M represents the mode class in D. Then, each unique class C in D is iterated through. The mode class of the dataset is kept constant. The mode class will be the class with the most occurrences.
(1)The Equation 1 is to calculate the new frequency, for the rest of the classes where posAway represents position away from the mode, and is stored in Frequency Dictionary . This equation is motivated by how the distribution is scaled away from the mode in the bell-curved symmetric. The author of SMOTE, Chawla et al. [6] have proven that between 200% and 300% oversampling rate is proven to be the most robust oversample ratio in SMOTE. Hence, we limit the amount to be oversample at 250% of the original frequency. With this, we can keep the naturally occurring distribution of the datasets and inherit the bias for training the models.
4. METHODOLOGY
4.1 Experimental Datasets
We use the same dataset from Figure 1. The selected datasets metadata can refer to [19]. To extract features for learning algorithms, we implement the Enhanced AI Scoring Engine (EASE) 2. We selected EASE as it is a robust feature engineering method for AES that several researchers have implemented in recent years [19, 16]. The EASE system will generate 14 features refer to [19]. Five-fold cross-validation is implemented to generate the train and test set due to unreleased test data from the ASAP competition. We redistributed the data into five-fold, where four-fold will be the train set and one-fold will be the test set in each round. Three different types of train set will be generated for the learning algorithms to train the models:
- (a)
-
Default. The train set with original distribution.
- (b)
-
Uniform Distribution. The train set is oversampled by SMOTE that makes the frequencies all classes to be uniformly same as the frequency of the mode class.
- (c)
-
GMC-SMOTE. The train set is oversampled by GMC-SMOTE to generate Gaussian-like distribution of the classes.
4.2 Learning Algorithm
The Bayesian Linear Ridge Regression (BLRR) algorithm is chosen among the other prospective methods such as Naive Bayes (NB) and Support Vector Machines (SVM) based on the results from Phandi et al. [19]. It allows a natural language processing tasks to deal with insufficient data by create linear regression through probability distributors instead of point estimate. Also, it is robust and has often delivers good results in natural language processing projects.
4.3 Evaluation Metric
We implement Quadratic Weighted Kappa (QWK) to calculate the rate of agreement among two graders; the human graders, and the scoring by the trained model. It varies from 0 to 1, where 0 represents no agreement, 0.01-0.20 as slight, 0.21-0.40 as fair, 0.41-0.60 as moderate, 0.61-0.80 as substantial, and 0.81-1.00 as almost perfect agreement [7]. QWK is proven to be robust since it takes into consideration the odds of accidental agreement [23]. Also, it is a common evaluation metric for AES models [19, 16].
5. RESULT AND DISCUSSION
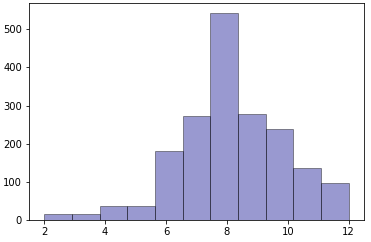
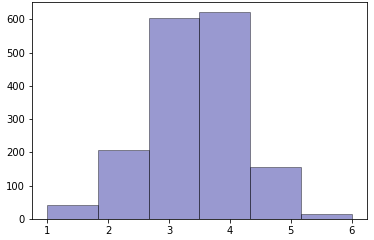
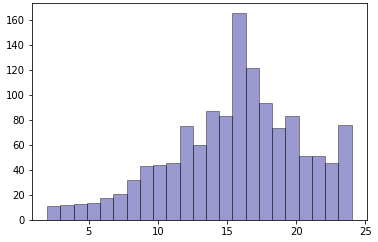
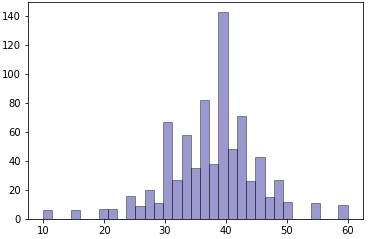
New samples for each essay set using the proposed GMC-SMOTE are generated. A sample of the GMC-SMOTE distribution histograms are plotted in Figure 2. From the observation on the Figure 1e and 1f, the new distributions are closer to a Gaussian distribution symmetrical on the left and right of the mode value. For the Figure 1g, the histogram is much flatter than the default distribution. As for Figure 1h, the data quality remains of concern due to missing data for many classes and low data samples. From all these observations, the nature of default distribution is inherited into the new distribution, which brings the inherent bias of default distribution to the new distribution.
We calculate the mean QWK scores for each trained model using the one-fold of test in five rounds. The results are shown in Table 1. The best result is bold-faced and the second best is underlined. Overall, the BLRR scores for GMC-SMOTE datasets are better than all the default datasets and GMC-SMOTE performs the best in essay sets 1, 2, and 8.
- Essay Set 1: An increase in QWK by 0.015 even though it has an almost perfect agreement using the default dataset.
- Essay Set 2: A more modest increase in QWK by 0.038, which is expected as the dataset distribution is similar and the number of classes are few.
- Essay Set 7: The GMC-SMOTE’s QWK is better than the default dataset but slight poorer than Uniform distribution dataset produced by the default SMOTE algorithm.
- Essay Set 8: A significant increase in QWK by 0.032 even though it has many missing classes and several classes with one to five frequency counts.
With the exception of essay set 7, the uniformly distributed datasets have poor results. This shows that simply applying SMOTE to the datasets has probably removed the inherent bias in an essay scoring situation. The proposed GMC-SMOTE has shown that with proper oversampling, maintaining the inherent scoring biasness in an academic setting can improve the automatic essay scoring agreement with the human graders. For essay set 7, although the GMC-SMOTE improved the QWK scores over the default dataset, the uniform distributed dataset has the best result. This can be attributed to the fact that the default dataset is relatively platykurtic with negative skewness. This encompasses the majority of the samples (scores of 15 or greater from Figure 1). Hence, applying a uniform distribution will enhance the sample and does not significantly impact the human scoring biasness. It will also mean that if there are sufficient sampling sizes, the naturally occurring distribution is the optimal distribution. This can be observed in Figure 2, for essay set 7, where the histogram is plotted for the new data distribution generated by GMC-SMOTE. Comparing the GMC-SMOTE distribution (Figure 2) with the default distribution (Figure 1), the naturally occurring distribution is kept in the new distribution while new samples are generated.
6. CONCLUSION
The results show that the GMC-SMOTE is an effective oversampling method for situations with some imbalance in the dataset. The proposed GMC-SMOTE method can be applied for training datasets for other classifications domains where the naturally occurring distribution is Gaussian (normal). Kurtosis and skewness can be used to assess the type of naturally occurring distribution of the respective dataset distribution. As observed in our evaluation (essay set 7), it is also important to first assess whether the kurtosis is much lesser than the normal distribution (platykurtic), which may require a uniformly distributed dataset. The assessment can be conducted prior to deciding whether to use Multi-Class SMOTE or the proposed GMC-SMOTE for imbalanced datasets.
7. REFERENCES
- E. L. Allwein, R. E. Schapire, and Y. Singer. Reducing multiclass to binary: A unifying approach for margin classifiers. Journal of machine learning research, 1(Dec):113–141, 2000.
- S. Barua, M. M. Islam, X. Yao, and K. Murase. Mwmote–majority weighted minority oversampling technique for imbalanced data set learning. IEEE Transactions on knowledge and data engineering, 26(2):405–425, 2012.
- R. C. Bhagat and S. S. Patil. Enhanced smote algorithm for classification of imbalanced big-data using random forest. In 2015 IEEE International Advance Computing Conference (IACC), pages 403–408. IEEE, 2015.
- C. M. Bishop. Pattern recognition. Machine learning, 128(9), 2006.
- F. Charte, M. J. del Jesus, and A. J. Rivera. Multilabel classification: problem analysis, metrics and techniques. Springer, 2016.
- N. V. Chawla, K. W. Bowyer, L. O. Hall, and W. P. Kegelmeyer. Smote: synthetic minority over-sampling technique. Journal of artificial intelligence research, 16:321–357, 2002.
- J. Cohen. A coefficient of agreement for nominal scales. Educational and psychological measurement, 20(1):37–46, 1960.
- C. Elkan. The foundations of cost-sensitive learning. In International joint conference on artificial intelligence, volume 17, pages 973–978. Lawrence Erlbaum Associates Ltd, 2001.
- A. Fernández, S. Garcia, F. Herrera, and N. V. Chawla. Smote for learning from imbalanced data: progress and challenges, marking the 15-year anniversary. Journal of artificial intelligence research, 61:863–905, 2018.
- A. F. Giraldo-Forero, J. A. Jaramillo-Garzón, J. F. Ruiz-Muñoz, and C. G. Castellanos-Domínguez. Managing imbalanced data sets in multi-label problems: a case study with the smote algorithm. In Iberoamerican Congress on Pattern Recognition, pages 334–342. Springer, 2013.
- H. Han, W.-Y. Wang, and B.-H. Mao. Borderline-smote: a new over-sampling method in imbalanced data sets learning. In International conference on intelligent computing, pages 878–887. Springer, 2005.
- T. Hastie, R. Tibshirani, et al. Classification by pairwise coupling. Annals of statistics, 26(2):451–471, 1998.
- H. He, Y. Bai, E. A. Garcia, and S. Li. Adasyn: Adaptive synthetic sampling approach for imbalanced learning. In 2008 IEEE international joint conference on neural networks (IEEE world congress on computational intelligence), pages 1322–1328. IEEE, 2008.
- V. Indira, R. Vasanthakumari, and V. Sugumaran. Minimum sample size determination of vibration signals in machine learning approach to fault diagnosis using power analysis. Expert Systems with Applications, 37(12):8650–8658, 2010.
- M. Kubat, S. Matwin, et al. Addressing the curse of imbalanced training sets: one-sided selection. In Icml, volume 97, pages 179–186. Citeseer, 1997.
- S. Latifi and M. Gierl. Automated scoring of junior and senior high essays using coh-metrix features: Implications for large-scale language testing. Language Testing, 38(1):62–85, 2021.
- X.-Y. Liu and Z.-H. Zhou. The influence of class imbalance on cost-sensitive learning: An empirical study. In Sixth International Conference on Data Mining (ICDM’06), pages 970–974. IEEE, 2006.
- D. Margineantu. When does imbalanced data require more than cost-sensitive learning. In Proceedings of the AAAI’2000 Workshop on Learning from Imbalanced Data Sets, pages 47–50, 2000.
- P. Phandi, K. M. A. Chai, and H. T. Ng. Flexible domain adaptation for automated essay scoring using correlated linear regression. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, pages 431–439, 2015.
- M. D. Shermis and J. C. Burstein. Automated essay scoring: A cross-disciplinary perspective. Routledge, 2003.
- M. A. Tahir, J. Kittler, and A. Bouridane. Multilabel classification using heterogeneous ensemble of multi-label classifiers. Pattern Recognition Letters, 33(5):513–523, 2012.
- J. S. Tan and I. K. Tan. Feature group importance for automated essay scoring. In International Conference on Multi-disciplinary Trends in Artificial Intelligence, pages 58–70. Springer, 2021.
- S. Vanbelle and A. Albert. A note on the linearly weighted kappa coefficient for ordinal scales. Statistical Methodology, 6(2):157–163, 2009.
- T. Wang, H. Li, Z. Li, and Z. Wang. A fast parameter estimation of generalized gaussian distribution. In 2006 8th international Conference on Signal Processing, volume 1. IEEE, 2006.
- D. L. Wilson. Asymptotic properties of nearest neighbor rules using edited data. IEEE Transactions on Systems, Man, and Cybernetics, (3):408–421, 1972.
© 2022 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.