ABSTRACT
Deep learning architectures such as RNN and pure-attention based models have shown state-of-the-art performance in modeling student performance, yet the sources of the predictive power of such models remain an open question. In this paper, we investigate the predictive power of aspects of LSTM and pure attention-based architectures that model sequentiality. We design a knowledge tracing model based on a general transformer encoder architecture to explore the predictive power of sequentiality for attention-based models. For the LSTM-based Deep Knowledge Tracing model, we manipulate the state transition coefficient matrix to turn sequential modeling on and off. All models are evaluated on four public tutoring datasets from ASSISTments and Cognitive Tutor. Experimental results show that DKT and pure-attention based models are overall insensitive towards removing major sequential signals by disabling their sequential modeling parts but with the attention-based model about four times more sensitive. Lastly, we shed light on benefits and challenges of sequential modeling in student performance prediction.
Keywords
1. INTRODUCTION
Bayesian and Deep Knowledge Tracing models use machine learning architectures with explicit representation of time slices that capture sequentiality. A new generation of models have emerged based on self-attention that have outperformed both BKT and DKT on the knowledge tracing task [9, 11, 19, 17, 7]. Interestingly, the transformer-based architecture that these models rely on has relatively weak modeling of the concept of a time-slice and subsequently of sequence. This prompts us to ask the question of what role sequentiality plays in the predictive performance of the latest generations of neural knowledge tracing models. Some of the better performing self-attention models adopt a combination of transformer and LSTM architectures, raising the question of if the LSTM is superior for capturing sequence-based signals. To investigate the role of sequentiality in the predictive power of the RNN-based DKT and transformer-based self-attention, or "contextual" models, we design experiments that compare two variants of each model; the original, a version in which time-components of the architecture are systematically disabled. Using four public datasets, we report each model’s sensitivity to removing signals of sequence. Our major contributions in this work are:
-
A simple, yet theoretically effective way of disabling attention-based models’ sequential modeling components.
-
A novel way of insulating DKT’s sequential modeling components to study it’s sequential modeling ability.
-
We find that DKT and BertKT are exceptionally robust to losing sequential modeling components in terms of performance.
2. RELATED WORK
For studying sequence effects for student performance prediction, Ding and Larson [4] showed that relative ordering of skills have negative effects on the performance of DKT. Kim et al. [10] studied DKT’s behavior by conducting a series of perturbation experiments on Monotonicity, Robustness and Convergence etc. Work prior to DKT has also studied sequencing effects, Pardos and Heffernan [13] used a modification of the BKT model to capture learning rates of ordered item pairs, finding that while statistically separable learning rates could be fit, this extra modeling of order did not significantly improve performance prediction accuracy.
Pure-attention based models such as Transformer [18] and Bidirectional Encoder Representations from Transformers (BERT) [3] were first introduced in the NLP field and achieved state of the art performance on major NLP tasks. These models, compared to LSTM predecessors, have the added advantage of enabling parallel training for computational efficiency [18] [2] and being better able to capture long term dependencies. Adapting these strengths to the knowledge tracing task, Self Attentive Knowledge Tracing (SAKT) [12] introduces the earlier attention-based models to solve student performance prediction. SAINT+ [14], which leverages various input features embeddings to assist tutoring on massive online learning platforms, and AKT [7] further improves the attention-based architecture by introducing monotonic attention and context-aware distance measure.
Hybrid sequential-contextual models have shown success. Last Query transformer RNN model [9] LSTM-SAKT [11] and MUSE [19] utilize the combination of transformer encoder and LSTM/GRU and achieved top-5 performance in a Kaggle AIEd Prediction Challenge 20201.
3. METHODOLOGY
3.1 Problem Restatement
Our study on sequential effects is based on the task of student performance prediction. We define this task as follows. Definition 1. Given a student ’s past interactive sequence from time step to that contains problem marked by required skill ids and their correctness of responses , performance prediction of problem of student at time step is defined as:
where and
3.2 The BertKT Architecture
To study the positional effect of transformer family of models,
we design a simple, general architecture named
Bidirectional encoder representations from transformers for
Knowledge Tracing, or BertKT. We design this model
instead of utilizing previously proposed models for several
reasons:
-
It does not contain redundant structures other than transformer encoder layers and an output layer for our downstream task. This helps us isolate the impact of sequential effects for attention-based models.
-
It adopts the most widely used sine-cosine positional encoding with easy enabling/disabling, which facilitates generalization of our results.
-
This architecture is flexible due to its simplicity to accommodate additional settings for future research.
In this work, we conduct student performance prediction in an auto-regressive fashion supported by an upper-triangular attention masks. We do not utilize the bi-directionality here, but such functionality could be enabled for future use such as for bi-directional pre-training tasks. Thus, we keep here the naming convention "bi-directional" as is.
3.2.1 Knowledge and Positional Encoding
In transformer models, scaled-dot-product self-attention which runs in [18]. Thus we adopt word embedding [1] in stead of one-hot encoding in the field of NLP to obtain a learnable knowledge encoding with higher computational efficiency. In this work, we only use skill and responses as input features. Embeddings of such features are element-wise-summed together to form a unified representation named combined embedding.
The transformer model is permutation-invariant [18, 5] without positional encoding, making it suffer from not being able to capture original sequence order. A wide varieties of positional encodings are introduced for better performance or interpretability[8, 7]. To study the effect of positionality in this type of model, we completely remove the sine-cosine positional encoding of our model introduced in section 3.2 and compare the model’s performance with the baseline model (positional encoding on).
3.2.2 BertKT encoder
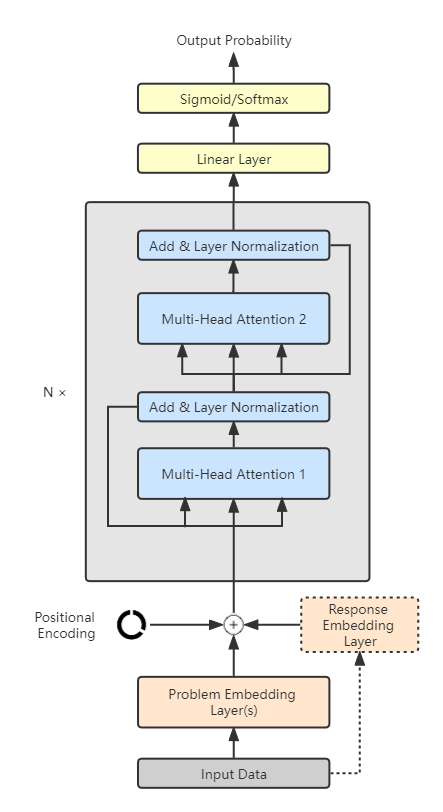
In section 3.2.1, we have introduced our element-wise-summed embedding. On top of that, we add a canonical transformer encoder to form the integrated BertKT Architecture. For computation flow, the skill embedding layer and the response embedding layer first take in skill ids and responses to compute their raw embeddings. These two embeddings together with positional encoding are summed element-wise to form a combined embedding. Secondly, the combined embedding goes through BertKT encoder to learn rich contextualized representations. Such contextualized embedding is further processed by linear output layers followed by sigmoid/softmax activation to output response predictions. The entire BertKT architecture can be viewed in Figure 1.
3.3 Manipulations of Sequential Factors
We manipulate the model structures to control the intensity of sequential signals learned in the hidden space. In terms of naming, we add the prefix static- to the resulting models with sequential signals modeling disabled.
3.3.1 Static BertKT
In this section, we describe a modification to BertKT’s positional encoding to explore sequential influences of the produced hidden space on the models’ performance. Specifically, we remove completely the sine-cosine positional encoding of BertKT and name it static-BertKT. For any position in a sequence ranging from attending to other items, the model can not distinguish the order of those items even if they are manually arranged in the correct order. This is because all other items are treated the same when computing attention regardless of their position. In such a sense, disabling the positional encoding is equivalent to disabling the exclusive indication for the model to capture explicit positionality. We compare the performance of BertKT and static BertKT in section 6.1.
3.3.2 Static DKT
In this section, we describe our modification to the sequential LSTM structures in DKT to observe performance changes due to effectively disabling weights associated with sequentiality modeling.
Static DKT Experiment
For DKT and all its variants we utilize in this work we employ
an LSTM as the core computational structure. The formula for
a canonical LSTM structure is as follows.
where
: input vector
of time step
:
forget gate
:
input gate
:
output gate
: hidden state
vector of time step
: cell
input
: cell
state
,
and
: learnable
weight and bias;
and
are the dimension of input features and that of hidden
states.
Concretely, the hidden state of time step is dependent on that of , the current input item at , but not on any future time step ranging from , where is the ending time step. Here we would like to disable the sequential, hidden-state transitioning dynamics to compare results with the original DKT model. Concretely, we set each of to an identity matrix . Obviously for any hidden state , an identity matrix multiplication equal to no transformation exerted at all. Also the could be combined with the bias term . However, we still keep matrix here for 2 reasons:
-
For the completeness of math formulation as this is a special case of the dynamic LSTM with learnable .
-
In terms of implementation, could be changed easily from a placeholder to other values for future research experiments.
In the end, we have the following static-LSTM as the new component of the corresponding DKT model we refer to as static-DKT.
where each gate update function remains the same but the explicit hidden state update is disabled.
Note that we do not hamper the sequential update format of cell state and hidden state , as they are part of the nature of a classic LSTM model. The hidden state is still sequentially updated but only implicitly through , , and . In summary, this experiment is to explore to what extent that sequential modeling factor of DKT contributes to its total predictive power in terms of evaluations metrics we introduce in section 5.2.
4. COMPARISON MODELS
In this section, we provide a reference table 1 to summarize the name of each model and their corresponding settings.
5. EXPERIMENTAL SETUP
5.1 Datasets
We evaluate the performance of BertKT and other comparison models based on four benchmark datasets: ASSISTments 2009-20102 [6], ASSISTments 2012-20133, Cognitive Tutor Bridge to Algebra 2006-20074 and Cognitive Tutor Bridge to Algebra 2008-20095 [15]. Among these benchmarks, ASSISTments datasets are collected from ASSISTments online tutoring system primarily for secondary school mathematics. Cognitive Tutor (now MATHia) is an intelligent tutoring system and the datasets we used are from its Algebra curricula. The two Cognitive Tutor datasets we use were used as the official development/competition dataset for the KDD Cup 2010 Challenge [16].
For all the above datasets, we follow a series of conventional pre-processing procedures such as removing all problems not associated with a concept/skill and using correct on first attempt responses only.
5.2 Models and Evaluation Metrics
We compare BertKT and DKT with their sequentiality-weakened counterparts. Differences and features of these model have been discussed in section 4; We evaluate each model across four metrics: BCE (Binary cross entropy loss), AUC (Area under the receiver operating characteristic curve), ACC (Accuracy as the proportion of correct classification with threshold 0.5) and RMSE (Root-mean-square error).
5.3 Training and Testing
We take out 20% of the entire data as the development set to conduct hyper-parameter tuning. For training and testing, We perform student-level -fold cross validation (with ) on each model, meaning each student will appear exclusively in training, validation or test set. In each phase of the cross validation, 60% of the dataset is used as the training set, 20% as the validation set to perform early stopping, and the rest 20% as the test set.
We fix a sequence length of 100 for computational efficiency with longer sequences split to subsequences of length 100 and trailing subsequence padded. We use Adam optimizer to update parameters for all models trained on two NVIDIA GeForce RTX 2080 Ti (11 GB) or TITAN Xp GPU (12 GB). All models are implemented using PyTorch with fixed random seeds for reproducibility.
6. EXPERIMENTAL RESULTS
In this section, we compare evaluations results of BertKT and DKT with their variants introduced in section 3. We report evaluation metrics per each model per metrics defined in section 5.2 as well as the relative percentage increase of these metrics between comparison models. Models with the best metrics are in bold. Specifically, we report the percentage increase by the "performance increase/decrease", meaning that increase in {BCE, RMSE} is marked by "-" and that increase in {AUC, ACC} is marked by "+". Decrease means the opposite way.
6.1 BertKT Model Results
Table 2 shows the evaluations metrics for BertKT and static-BertKT. The best performances by metric are in bold. We have explained the meanings of these variant models in table 1. Overall, the baseline BertKT performs better, with 10 bolded cells, than its sequentially disrupted variants. However, the percentage performance differences averaged over the four dataset benchmarks of static-BertKT from BertKT are -0.64%, -0.19%, -0.02%, -0.24% for BCE, AUC, ACC and RMSE, respectively (’+’ indicates a performance improvement for the metric, while ’-’ represents a performance decrease). This suggests that BertKT is insensitive towards sequential permutation even without positional encoding.
6.2 DKT Model Results
In this section, we compare in table 3 DKT with its sequentially weakened counterpart, namely, DKT and static-DKT. Naming conventions have been introduced in table 1 in section 4.
Surprisingly, the static-DKT model was the best performing model on all datasets for all but one metric of one dataset (ASSISTments 2009-AUC). The average percentage performance differences averaged over the four dataset benchmarks of static-DKT from DKT are +0.13%, +0.04%, +0.07%, +0.09% for BCE, AUC, ACC and RMSE, respectively (’+’ indicates a performance improvement for the metric, while ’-’ represents a performance decrease). Even after disabling weights associated with time-slice transitions, the model performs closely to the baseline model and even with a slight increase. This suggests that the embedding weights for input X , , and are still sufficient to capture signals that support the model’s original performance.
Across the four metrics and four datasets, DKT improves 0.08% due to a static hidden state transition, while the performance of BertKT decreases by 0.27% due to no positional encoding (static). The average percentage performance loss of BertKT due to being static is -4.3340x larger than that of DKT. This suggests BertKT’s positional encoding is more sensitive in modeling the sequence order than DKT in terms of performance.
7. CONCLUSIONS AND DISCUSSION
While our motivating observation was that transformer-based models have weaker explicit modeling of time than LSTM-based models, we find that BertKT is more dependent on its positional encoding than DKT is on its time-slice transition weights. Such sensitivity may be an indication that there is room for improvement for positional encodings to better leverage input sequence order. This improvement is perhaps seen in the performance of AKT [7], which outperforms DKT and employs additional modeling of sequentiality in the form of imposed monotonicity of attention weights with respect to time.
Our results raise the question of why DKT is not negatively affected by disabling its transition weights. Potentially, the temporal signal is being pushed down into the embedding . Is student growth better captured in the interactions between input embeddings than it is by a generalized recurrent hidden state transition? This may speak to the powerful but simple assumption of the original knowledge tracing model, that learning is a function of opportunity count, growth rate, and prior.
8. REFERENCES
- Y. Bengio, R. Ducharme, P. Vincent, and C. Janvin. A neural probabilistic language model. The journal of machine learning research, 3:1137–1155, 2003.
- C. Chen and Z. Pardos. Applying recent innovations from nlp to mooc student course trajectory modeling. In Proceedings of the 13th International Conference on Educational Data Mining, 2020.
- J. Devlin, M.-W. Chang, K. Lee, and K. Toutanova. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805, 2018.
- X. Ding and E. C. Larson. Why deep knowledge tracing has less depth than anticipated. In Proceedings of the 12th International Conference on Educational Data Mining, 2019.
- P. Dufter, M. Schmitt, and H. Schütze. Position information in transformers: An overview. arXiv preprint arXiv:2102.11090, 2021.
- M. Feng, N. Heffernan, and K. Koedinger. Addressing the assessment challenge with an online system that tutors as it assesses. User Modeling and User-Adapted Interaction, 19(3):243–266, 2009.
- A. Ghosh, N. Heffernan, and A. S. Lan. Context-aware attentive knowledge tracing. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pages 2330–2339, 2020.
- Z. Huang, D. Liang, P. Xu, and B. Xiang. Improve transformer models with better relative position embeddings. In Findings of Empirical Methods in Natural Language Processing, 2020.
- S. Jeon. Last query transformer rnn for knowledge tracing. In Workshop on AI Education@35th AAAI Conference on Artificial Intelligence, 2021.
- M. Kim, Y. Shim, S. Lee, H. Loh, and J. Park. Behavioral testing of deep neural network knowledge tracing models. In Proceedings of the 14th International Conference on Educational Data Mining, 2021.
- T. Oya and S. Morishima. Lstm-sakt: Lstm-encoded sakt-like transformer for knowledge tracing. In Workshop on AI Education@35th AAAI Conference on Artificial Intelligence, 2021.
- S. Pandey and G. Karypis. A self-attentive model for knowledge tracing. In Proceedings of the 12th International Conference on Educational Data Mining, 2019.
- Z. A. Pardos and N. T. Heffernan. Determining the significance of item order in randomized problem sets. In T. Barnes, M. C. Desmarais, C. Romero, and S. Ventura, editors, Educational Data Mining - EDM 2009, Cordoba, Spain, July 1-3, 2009. Proceedings of the 2nd International Conference on Educational Data Mining, pages 111–120. www.educationaldatamining.org, 2009.
- D. Shin, Y. Shim, H. Yu, S. Lee, B. Kim, and Y. Choi. Saint+: Integrating temporal features for ednet correctness prediction. In Proceedings of the 11th International Learning Analysis and Knowledge Conference, 2021.
- J. Stamper, A. Niculescu-Mizil, S. Ritter, G. Gordon, and K. Koedinger. Bridge to algebra 2008-2009. challenge data set. In KDD Cup 2010 Educational Data Mining Challenge, 2010.
- J. Stamper and Z. A. Pardos. The 2010 kdd cup competition dataset: Engaging the machine learning community in predictive learning analytics. Journal of Learning Analytics, 3(2):312–316, 2016.
- D. K. L. Tran. Riiid! answer correctness prediction kaggle challenge: 4th place solution summary. In Workshop on AI Education@35th AAAI Conference on Artificial Intelligence, 2021.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, and I. Polosukhin. Attention is all you need. In Advances in neural information processing systems, pages 5998–6008, 2017.
- C. Zhang, Y. Jiang, W. Zhang, and C. Gu. Muse: Multi-scale temporal features evolution for knowledge tracing. In Workshop on AI Education@35th AAAI Conference on Artificial Intelligence, 2021.
1https://www.kaggle.com/c/riiid-test-answer-prediction
2https://drive.google.com/file/d/1NNXHFRxcArrU0ZJSb9BIL56vmUt5FhlE/view?usp=sharing
3https://drive.google.com/file/d/1cU6Ft4R3hLqA7G1rIGArVfelSZvc6RxY/view?usp=sharing
© 2022 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.