ABSTRACT
Knowledge Tracing (KT), the task of tracing students’ knowledge state, has attracted attention in the field of artificial intelligence. Recently, many researchers have proposed KT methods using deep learning to predict student performance on unknown tasks based on learning history data. Especially, the latest DeepIRT reportedly has high predictive accuracy and parameter interpretability. Nevertheless, some room remains for improvement of its prediction accuracy because it does not optimize the degree of forgetting of past data. Specifically, although its forgetting parameters are optimized solely using current input data, it should use both current input and past data to optimize them. Therefore, for better parameter estimation to improve accuracy, this study proposes a new DeepIRT that optimizes the degree of forgetting of past data. The proposed method has a hypernetwork to balance both the current and the past data in memory, which stores a student’s knowledge states. Results of experiments demonstrate that the proposed method improves the prediction accuracy compared to earlier KT methods.
Keywords
1. INTRODUCTION
Recently, with the development of online education [24, 25, 26], Knowledge Tracing (KT) has attracted broad attention for helping students to learn effectively by presenting optimal problems and a teacher’s support. [3, 7, 10, 15, 16, 17, 28, 29, 33, 34, 35]. Important tasks of KT are tracing the student’s evolving knowledge state and discovering concepts that the student has not mastered based on the student’s past learning history data. Furthermore, accurate prediction of a student’s performance (correct or incorrect response to an unknown item) is important for adaptive learning. Although KT methods have been proposed as probabilistic approaches [3, 7, 28, 29, 34] and deep-learning-based approaches [17, 28, 29, 33, 35], the latter have been studied more actively in recent years because they reportedly have high prediction accuracies.
Various deep-learning-based approaches have been proposed to improve the prediction accuracy of a student’s performance[1, 20, 21, 32]. Most recently, Ghosh et al. (2020) proposed attentive knowledge tracing (AKT) [6], which incorporates a forgetting function of past data to attention mechanisms: the Transformer method [27]. In addition, AKT optimizes the parameters to weight the data necessary for student performance prediction from past learning data. Therefore, AKT has the best performance for predicting a student’s responses among earlier KT methods. However, the interpretability of the parameters is limited because it cannot express a student’s ability transition of each skill [6, 14, 22].
On the other hand, to express a student’s the knowledge state transition for deep-learning-based approaches, Zhang proposed the dynamic key-value memory network (DKVMN) [35]. DKVMN traces the knowledge state transition using a Memory-Augmented Neural Network and attention mechanisms. It can estimate the relations between underlying skills and items addressed by students. In addition, DKVMN has a memory updating component to allow forgetting and updating of the latent variable memory, which stores the students’ knowledge states in the learning process [35]. For interpretability of the parameters, the memory updating component in DKVMN is more effective than the forgetting function of AKT because it updates the current latent variable memory, which stores the students’ skills and abilities, using only the immediately preceding values.
To improve the interpretability of the parameters of DKVMN, DeepIRT was proposed by combining DKVMN with an Item Response Theory (IRT) [2, 11, 30] module [33]. It includes the students’ ability parameters and the items’ difficulty parameters. However, it was insufficient to improve the interpretability because a student’s ability of DeepIRT depends on each item characteristic. To resolve this shortcoming, Tsutsumi et al. proposed DeepIRT methods with independent redundant student and item networks [22, 23]. They can learn the student’s ability and item difficulty independently to avoid impairing the predictive accuracy. For DeepIRT [23], a student’s ability is constant throughout a learning process because it is structured for test theory. Therefore, it can not be applied to KT. To apply DeepIRT to KT, DeepIRT [22] was proposed using architecture of DKVMN. In DeepIRT [22], a student network employs memory network architecture to reflect dynamic changes of student abilities as DKVMN does. Because the student’s ability parameters of the DeepIRT [22] are independent of each item characteristic, it has higher interpretability than the earlier method has [33]. Furthermore, the DeepIRT [22] can express a student’s ability transition for each skill by estimating relations among the multidimensional skills. Consequently, the DeepIRT provides high interpretability without impairing the predictive accuracy.
However, room for improvement of prediction accuracy of the DeepIRT remains [22] because it does not optimize the degree of forgetting the past data. Specifically, in DKVMN and DeepIRT methods, the forgetting parameters which control the degree of forgetting the past data are optimized from only the current input data: the student’s latest response to an item. As a result, it might degrade the prediction accuracy of the DeepIRT because the value memory insufficiently reflects the past learning history data. Namely, it might be difficult to reflect the past data accurately in a long learning process. It should use not only the current input data but also past data to optimize the forgetting parameters.
In this study, we propose the new DeepIRT with a hypernetwork to optimize the forgetting parameters. The hypernetwork [5, 4, 8, 9, 12, 13, 19, 31] balances both current and the past data in the latent variable memory, which stores a student’s knowledge state data. Before the model updates the latent variable memory, it optimizes not only the weights of the forgetting parameters but also the past latent variable memory. Experiments were conducted to compare the performances of the proposed method and those of the earlier KT methods. The results demonstrate that the proposed method improves the prediction accuracy of the DeepIRT [22]. They also indicate the proposed method as effective, especially for tasks with a long-term learning process.
2. DKVMN AND DEEP-IRT METHODS
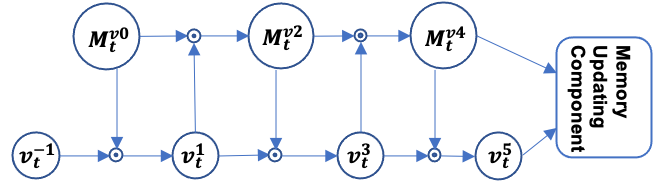
DKVMN and DeepIRT methods [22, 33, 35] have the same memory updating component to update and forget the students’ knowledge states in the learning process [35]. The value memory , which traces the process of student ability growth, is updated in this memory updating component. They use based on input , which reflects a latest student’s response data to item at time .
(1)Here, is a zero vector consisting of zero values. They updated the value memory as
and
where and are the weight matrices, and and are the bias vectors. Furthermore, signifies the degree of strength of the relations between the underlying skill and skill tags addressed by a student at time . It is noteworthy that , and are forgetting parameters, which adjust the degrees of forgetting the past data and reflecting the current input data. influences how much the value memory forgets (remembers) the past ability. Additionally, controls how much the value memory reflects the current input data.
For the interpretability of the parameters, this memory updating component is more effective than the forgetting function of AKT because it updates the current latent variable memory which stores the student’s skills and abilities using only the immediately preceding values. However, the forgetting parameters are optimized only from current input data. It should use not only the current input data but also past data to optimize them. Additionally, the weights are fixed values and are not optimized for each time point. As a result, DKVMN and DeepIRT might degrade the prediction accuracies because of value memory which only insufficiently reflects past learning history data. Especially, it might be difficult to reflect past data accurately in a long learning process.
3. PROPOSED METHOD
The preceding section described that the forgetting parameters of DeepIRT are not optimized using both current input data and past data. However, when using both current input data and past data, it is difficult to optimize the weight parameters directly because the number of parameters increases dynamically.
Recent studies in the field of Natural Language Processing (NLP) proposed the extension components to LSTM [18] in the form of mutual gating of the current input data and the previous output hidden variables [4]. These extension components are called hypernetworks. A hypernetwork supports the main recurrent neural network by optimizing the non-shared weights for each time point in the hidden layers [4]. In standard LSTM [18], the hidden variables change with time, but the weights used to update them are fixed values and are not optimized for each time point. To resolve this difficulty, various hypernetworks have been proposed to optimize the non-shared weights in the LSTM at each time point. [5, 4, 8, 9, 12, 13, 31]. Their results demonstrate that LSTM with a hypernetwork works better than the standard LSTM [18].
Melis et al. earlier proposed the "Mogrifier component" which is a kind of hypernetwork for LSTM in the field of NLP [12]. Mogrifier also scales the weights and the hidden variables using not only the current inputs but also the output of the hidden variable at the previous point in time. They reported that the LSTM with Mogrifier component outperforms the other methods for a long input data length. Inspired by those studies, this study proposes a new hypernetwork that optimizes the degree of forgetting of past data in the DeepIRT [22] to improve prediction accuracy with the parameter interpretability. We incorporate the proposed hypernetwork in the memory updating component, which updates the latent variable , to avoid greatly increasing number of parameters. Before the model updates the latent variable , the proposed hypernetwork optimizes not only the weights of the forgetting parameters but also the past latent variable . The proposed hypernetwork estimates the optimal forgetting parameters by balancing both the current input data and the past latent variable. In adition, the Mogrifier component [12] used constant values as the tuning parameters in the hypernetwork. For this study, we optimize the tuning parameters to adjust the hypernetwork for each dataset. No report of the relevant literature has described a study of the use of the hypernetworks for KT methods. Figure 1 presents the architecture of the proposed method. The right side of Figure 1 presents the hypernetworks and the memory updating component. The left side of Figure 1 shows the independent student and item networks.
3.1 Hypernetwork
To optimize the forgetting parameters at time , the proposed hypernetwork balances the current input data and the past value memory to store sufficient information of the learning history data before calculating the latent variables . The proposed hypernetwork structure is located at the beginning of the Memory Updating Component on the right side of Figure 1 (shown in red).
Figure 2 shows the structure of the proposed hypernetwork. The inputs of the hypernetwork are the past value memory and current input data when a student responds to item of skill . Therein, represents the number of skills. The embedding vector of denoted as . Because of the repeating multiplications as shown in Figure 2, this hypernetwork balances current data and past value memory . For the proposed methods, we optimize the number of rounds for each learning dataset.
3.2 Memory Updating Component
Next, we estimate the forgetting parameters and using the optimized and in the hypernetwork. These forgetting parameters are important to update the latest value memory optimally. The earlier memory updating component of DKVMN and DeepIRT methods calculates the forgetting parameters from with only current input information in equation (3), (4). By contrast, we calculate them using the optimized current input data and the past latent value . Therefore, the forgetting parameters , and are also be estimated as optimizing the degree of forgetting of past data and as reflecting the current input data. Furthermore, the proposed method can capture the student knowledge state changes accurately because the latent knowledge state has sufficient information of the past learning history data.
4. EXPERIMENTATION
4.1 Datasets and Experiment Setting
This section presents comparisons of the prediction accuracies of the proposed method with those of earlier methods (Tsutsumi et al. and AKT) [6, 22]. We use two standard benchmark datasets ASSISTments2009 and ASSISTments2017 collected from an online tutoring system. Table 1 presents the number of students (No. Students), the number of skills (No. Skills), the number of items (No. Items), the rate of correct responses (Rate Correct), and the average length of the items which students addressed (Learning length).
We used five-fold cross-validation to evaluate the prediction accuracies of the methods. The item parameters and hyperparameters are trained by 70% of each dataset. Given the estimated parameters, the students’ abilities are estimated at each time using the remaining 30% of each dataset according to an earlier study [22]. We employ Adam optimization with a learning rate of 0.003 and batch-size 32. Additionally, 200 items was set as the upper limit of the input length according to the earlier studies [22, 33, 35]. For this study, we leverage three metrics for prediction accuracy: Accuracy (Acc) score, AUC score, and Loss score.
4.2 Prediction Accuracy
The respective values of Acc, AUC, and Loss for ASSISTments2009 and ASSISTments2017 datasets [6, 22] are presented in Table 2. We compared the performances of the proposed method with those of DeepIRT [22] and AKT for each dataset with item and skill tag inputs according to [6]. Additionally, this report describes the standard deviations across five test folds.
Results indicate that the proposed method, which optimizes the forgetting parameters, provides the best average scores for all metrics. Especially, the proposed method outperforms the Tsutsumi el al. [22] and AKT for ASSISTments2017. ASSISTments2017 has a long learning length. By contrast, the proposed method tends to have lower prediction accuracies for ASSISTments2009 with a shorter learning length than AKT has. Results suggest that the proposed hypernetwork functions effectively, especially for datasets with long learning lengths.
| Dataset | No. students | No. skills | No. Items | Rate Correct | Learning length |
|---|---|---|---|---|---|
| ASSISTments2009 | 4151 | 111 | 26684 | 63.6% | 52.1 |
| ASSISTments2017 | 1709 | 102 | 3162 | 39.0% | 551.0 |
| Dataset | metrics | Tsutsumi et al. | AKT | Proposed |
|---|---|---|---|---|
| AUC | 80.70 +/- 0.56 | 82.20 +/- 0.25 | 81.57 +/- 0.39 | |
| ASSISTments2009 | Acc | 76.13 +/- 0.58 | 77.30 +/- 0.55 | 76.85 +/- 0.56 |
| Loss | 0.54 +/- 0.10 | 0.49 +/- 0.10 | 0.53 +/- 0.13 | |
| AUC | 74.15+/- 0.27 | 74.54+/- 0.21 | 76.85 +/- 0.39 | |
| ASSISTments2017 | Acc | 68.73+/- 0.11 | 69.83+/- 0.15 | 71.08 +/- 0.50 |
| Loss | 0.57+/- 0.06 | 0.58+/- 0.06 | 0.55 +/- 0.06 | |
| AUC | 77.42 | 78.37 | 79.21 | |
| Average | Acc | 72.43 | 73.56 | 74.00 |
| Loss | 0.56 | 0.54 | 0.54 |
5. CONCLUSIONS
Recently, to express a student’s the knowledge state transition for deep-learning-based approaches, DKVMN and Deep-IRT methods have been proposed. Tsutsumi et al. (2021) proposed a DeepIRT with independent redundant student and item networks [22]. It can learn the student’s ability and item difficulty independently to avoid impairing the predictive accuracy. Furthermore, the DeepIRT [22] can express a student’s ability transition for each skill by estimating relations among the multidimensional skills. the DeepIRT [22] has a memory updating component to allow forgetting and updating of the latent variable memory, which stores the students’ knowledge states in the learning process. However, the forgetting parameters which control the degree of forgetting the past data are optimized from only the current input data. It might degrade the prediction accuracy of the DeepIRT because the value memory insufficiently reflects the past learning history data. It should use not only the current input data but also past data to optimize the forgetting parameters.
This study proposed a new DeepIRT with a hypernetwork that optimizes the degree of forgetting of the past data for parameter estimation to improve prediction accuracy with the parameter interpretability. In the proposed method, the hypernetwork balances the current input data and the past value memory to store sufficient information of the learning history data before calculating the latent variables. Specifically, it scales not only the weights of the forgetting parameters but also the hidden variables using the current inputs and the output of the hidden variable at the previous point in time.
Experiments conducted with the benchmark datasets demonstrated that the proposed method improves the prediction accuracies of the earlier KT methods. Especially, results showed that the proposed method is effective for tasks with a long-term learning process. As future work, we will evaluate the interpretability of the ability parameters of the proposed method by comparing the parameter estimates with those of the earlier DeepIRTs [22, 33]. Furthermore, we will clarify the mechanism of how the proposed hypernetwork functions to increase the predictive accuracy.
6. ACKNOWLEDGMENTS
This research was supported by JSPS KAKENHI Grant Numbers JP19H05663, JP19K21751 and JP22J15279.
7. REFERENCES
- F. Ai, Y. Chen, Y. Guo, Y. Zhao, Z. Wang, G. Fu, and G. Wang. Concept-aware deep knowledge tracing and exercise recommendation in an online learning system. In EDM, 2019.
- F. Baker and S. Kim. Item Response Theory: Parameter Estimation Techniques, Second Edition. Statistics: A Series of Textbooks and Monographs. Taylor & Francis, 2004.
- A. T. Corbett and J. R. Anderson. Knowledge tracing: Modeling the acquisition of procedural knowledge. User Model. User-Adapt. Interact., 4(4):253–278, Dec 1995.
- H. David, D. Andrew, and V. L. Quoc. Hypernetworks. arXiv preprint arXiv:1609.09106, 2016.
- C. Fernando, D. Banarse, M. Reynolds, F. Besse, D. Pfau, M. Jaderberg, M. Lanctot, and D. Wierstra. Convolution by evolution: Differentiable pattern producing networks. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO), pages 109–116, 07 2016.
- A. Ghosh, N. Heffernan, and A. S. Lan. Context-aware attentive knowledge tracing. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2020.
- M. Khajah, Y. Huang, J. Gonzalez-Brenes, M. Mozer, and P. Brusilovsky. Integrating knowledge tracing and item response theory: A tale of two frameworks. Personalization Approaches in Learning Environments, 1181:5–17, 2014.
- J. Koutník, F. Gomez, and J. Schmidhuber. Evolving neural networks in compressed weight space. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO), pages 619–626, 01 2010.
- B. Krause, L. Lu, I. Murray, and S. Renals. Multiplicative lstm for sequence modelling. Workshop Track in ICLR, 2017.
- J. Lee and E. Brunskill. The impact on individualizing student models on necessary practice opportunities. In Proceedings of the Fifth International Conference on Educational Data Mining, pages 118–125, 01 2012.
- F. Lord and M. Novick. Statistical Theories of Mental Test Scores. Addison-Wesley, 1968.
- G. Melis, K. Tomáš, and B. Phil. Mogrifier lstm. In Proceedings of ICLR 2020, 2020.
- M. Moczulski, M. Denil, J. Appleyard, and N. Freitas. Acdc: A structured efficient linear layer. In ICLR, 2016.
- S. Pandey and G. Karypis. A self-attentive model for knowledge tracing. In Proceedings of International Conference on Education Data Mining, 2019.
- Z. Pardos and N. Heffernan. T.: Modeling individualization in a bayesian networks implementation of knowledge tracing. In In Proceedings of the 18th International Conference on User Modeling, Adaption, and Personalization, pages 255–266, 06 2010.
- Z. Pardos and N. Heffernan. Kt-idem: Introducing item difficulty to the knowledge tracing model. In Proceedings of 19th International Conference on User Modeling, Adaptation and Personalization (UMAP 2011), pages 243–254, 01 2011.
- C. Piech, J. Bassen, J. Huang, S. Ganguli, M. Sahami, L. J. Guibas, and J. Sohl-Dickstein. Deep knowledge tracing. In C. Cortes, N. D. Lawrence, D. D. Lee, M. Sugiyama, and R. Garnett, editors, Advances in Neural Information Processing Systems 28, pages 505–513. Curran Associates, Inc., 2015.
- H. Sepp and S. Jurgen. Long short-term memory. Neural Computation, 14:1735–1780, 1997.
- K. Stanley, D. D’Ambrosio, and J. Gauci. A hypercube-based encoding for evolving large-scale neural networks. Artificial life, 15:185–212, 02 2009.
- Y. Su, Q. Liu, Q. Liu, Z. Huang, Y. Yin, E. Chen, C. H. Q. Ding, S. Wei, and G. Hu. Exercise-enhanced sequential modeling for student performance prediction. In AAAI, pages 2435–2443, 2018.
- X. Sun, X. Zhao, Y. Ma, X. Yuan, F. He, and J. Feng. Multi-behavior features based knowledge tracking using decision tree improved dkvmn. In Proceedings of the ACM Turing Celebration Conference – China, New York, NY, USA, 2019. Association for Computing Machinery.
- E. Tsutsumi, R. Kinoshita, and M. Ueno. Deep-irt with independent student and item networks. In Proceedings of the 14th International Conference on Educational Data Mining (EDM), 2021.
- E. Tsutsumi, R. Kinoshita, and M. Ueno. Deep item response theory as a novel test theory based on deep learning. Electronics, 10(9), 2021.
- M. Ueno. Data mining and text mining technologies for collaborative learning in an ILMS "samurai". In Proceedings of the IEEE International Conference on Advanced Learning Technologies, ICALT 2004, pages 1052–1053, 2004.
- M. Ueno and Y. Miyazawa. Probability based scaffolding system with fading. In Proceedings of Artificial Intelligence in Education – 17th International Conference, AIED, pages 237–246, 2015.
- M. Ueno and Y. Miyazawa. IRT-based adaptive hints to scaffold learning in programming. IEEE Transactions on Learning Technologies, 11:415–428, 10 2018.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser, and I. Polosukhin. Attention is all you need. pages 5998–6008, 2017.
- X. Wang, J. Berger, and D. Burdick. Bayesian analysis of dynamic item response models in educational testing. The Annals of Applied Statistics, 7(1):126–153, 2013.
- R. Weng and D. Coad. Real-time bayesian parameter estimation for item response models. Bayesian Analysis, 13, 12 2016.
- W.J. van der Linden. Handbook of Item Response Theory, Volume Two: Statistical Tools. Chapman and Hall/ CRC Statistics in the Social and Behavioral Sciences. Chapman and Hall/ CRC, 2016.
- Y. Wu, S. Zhang, Y. Zhang, Y. Bengio, and R. Salakhutdinov. On multiplicative integration with recurrent neural networks. In Advances in neural information processing systems, pages 2856–2864, 2016.
- X. Xiong, S. Zhao, V. Inwegen, E. G., and J. E. Beck. Going deeper with deep knowledge tracing. In Proceedings of International Conference on Education Data Mining, 2016.
- C. Yeung. Deep-irt: Make deep learning based knowledge tracing explainable using item response theory. In Proceedings of the 12th International Conference on Educational Data Mining, EDM, 2019.
- M. V. Yudelson, K. R. Koedinger, and G. J. Gordon. Individualized bayesian knowledge tracing models. In Artificial Intelligence in Education, pages 171–180, Berlin, Heidelberg, 2013. Springer Berlin Heidelberg.
- J. Zhang, X. Shi, I. King, and D.-Y. Yeung. Dynamic key-value memory network for knowledge tracing. In Proceedings of the 26th International Conference on World Wide Web, WWW ’17, pages 765–774, Republic and Canton of Geneva, CHE, 2017. International World Wide Web Conferences Steering Committee.
© 2022 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.