ABSTRACT
Working collaboratively in groups can positively impact performance and student engagement. Intelligent social agents can provide a source of personalized support for students, and their benefits likely extend to collaborative settings, but it is difficult to determine how these agents should interact with students. Reinforcement learning (RL) offers an opportunity for adapting the interactions between the social agent and the students to better support collaboration and learning. However, using RL in education with social agents typically involves training using real students. In this work, we train an RL agent in a high-quality simulated environment to learn how to improve students’ collaboration. Data was collected during a pilot study with dyads of students who worked together to tutor an intelligent teachable robot. We explore the process of building an environment from the data, training a policy, and the impact of the policy on different students, compared to various baselines.
Keywords
1. INTRODUCTION
Pedagogical agents have demonstrated the potential to positively impact student learning and motivation in an educational setting [38, 39]. They are commonly characterized as either physical robots or virtual agents and provide an extra opportunity for students to have a social, interactive, and personalized learning experience. Pedagogical agents can be scaled by deploying multiple instances for students to use. While robots are not as easily deployed as virtual agents, recent research suggests that robots can be more effective than virtual agents in engaging students [32]. There is increasing interest in understanding how robots might play a role in formal and informal learning environments [31, 40].
One potential advantage of a robotic agent over a virtual agent is its ability to physically interact with the students. Some work has explored the use of robots capable of facial expressions and found its behavior increased the learning efficiency of students [51]. It had been observed that the physical embodiment of a robotic agent resulted in a higher level of social influence [46]. Other work has explored using gestures from a humanoid robot to help provide feedback to students about multiplication table problems [30].
Robots can take on multiple roles in interactions with a learner, including a tutor, a peer learner, or a tutee [4]. When robots take on the role of tutee, they are often called teachable robots. There are examples of success with teachable robots and a single student [23, 59, 37]. However, there has been less exploration of the use of teachable robots in a collaborative learning setting [12], with a student dyad [58]. This is a limitation of prior work since student collaboration is a powerful tool for improving learning [8, 14, 41]. Collaboration among peers in a computer-supported group setting can be supported by specially designed tasks that encourage interaction. [13]. Computer-supported group settings can encourage collaboration by targeting specific areas and difficulties of group interaction [57].
There are many ways that pedagogical agents adapt and personalize to students. One standard method is a statistical approach, such as multi-armed-bandit [11, 53], but these approaches have some trade-offs [47]. These systems require task-specific expert-authored rules; this may not be a sustainable approach for multi-disciplinary use. In contrast, a data-driven and automated approach is an exciting new way of understanding how to implement personalization.
Reinforcement learning (RL) is a data-driven approach for learning a policy for interacting with the students [44]. While multi-armed bandit approaches identify one action as the best and only select that action, RL policies use context about their environment to choose the best action for a specific moment1. Traditionally, reinforcement learning uses a virtual environment, which is used to train an initial policy, that is then transferred to the real world.
The RL-controlled robotic tutor described in Park et al. [44] does not involve the use of a virtual environment to train, instead training directly on the students. The experiences collected are always using the latest iteration of the policy, which is continually changing. While real-world RL ensures that the students interact with the most up-to-date policy, it actively uses students to test potentially sub-optimal actions during training, which might lead to confusion and unnatural interactions. With this approach, the policy learns through extensively interacting with students, requiring many months of training and needs to build a profile about each student. Real-world RL is also well-known as being particularly challenging [16].
Learning an RL policy in a virtual environment has two main benefits over real-world reinforcement learning. A policy can be trained in just a few hours by simulating millions of different versions of the environment and their outcomes. Furthermore, by training solely in a simulation, there is no need to train a policy through extensive experimentation on students. However, building such a simulation of the real world is challenging. One solution is offline reinforcement learning, in which an algorithm learns from a set of previously collected data, which obviates the need for a simulated virtual environment. Unfortunately, offline reinforcement learning requires an extensive collection of saved experience data [17], which is infeasible to collect from students.
We, therefore, assume a hybrid approach, using the set of previously collected data to model and build a data-driven simulation, effectively allowing for online reinforcement learning in an offline reinforcement learning setting. We explore the process of building a high-quality data-driven virtual environment, the difficulties in modeling the students, and ensuring environmental continuity.
We aim to see how a pedagogical robot can assist students in a group setting. The humanoid robot interacts with two students concurrently, as a social learning companion. We attempt to use Reinforcement Learning to aid in the decisions made by the teachable robot, to improve student learning outcomes and motivation by supporting students in a personalized manner.
The robot, named Emma, interacts with students via natural language. As the students work out the multi-step problems, they explain their solutions to Emma. Emma responds to the students’ solutions, clarifying the purpose of the most recent step or occasionally asking thought-provoking follow-up questions. These actions are combined with gestures to make interacting with the robot feel more natural.
Student interactions with Emma were collected using an expert-authored natural language dialogue script. We built a simulation describing the interactions between the students and modeled the different types of interactions those students had with Emma. The simulation uses collected data to represent various types of student groups.
Extensive testing of the policies trained and tested in the simulation demonstrates that RL methods outperform the dialogue script baseline in terms of collaboration metrics. Furthermore, in our simulation, we find that the RL methods improve collaboration among all student groups, unlike our baseline method, which fails to improve collaboration for some groups. Our contributions include:
- A hybrid approach to perform offline RL in a robot-student setting using online RL trained in a virtual environment.
- A novel method for building a virtual environment from previously collected data, to simulate student collaboration.
- An early exploration of applying RL for a teachable robotic agent in a collaborative setting with students.
2. BACKGROUND
Reinforcement Learning (RL) has provided recent breakthroughs in solving complex machine learning tasks, highlighted by applications in self-driving vehicles [29], superhuman performance in competitive board and video games [54, 55], and advanced autonomous robotic control [1, 42]. RL allows an agent or policy to sequentially select actions to achieve some (potentially non-differentiable) goal.
Reinforcement Learning differs from the more traditional supervised learning, where a classifier is exposed to a set of labeled examples, with the goal of correctly classifying an unseen example. There is often no label or ground truth for what actions are right or wrong for an RL agent to select in the settings where reinforcement learning is used. Additionally, each action may have cascading effects on the environment’s future, and similar actions may have varying effects that depend on the current state of the environment.
The policy in RL is a function, typically modeled with a neural network, that selects actions to navigate some environment given information about the current state of the environment and a reward that grades the actions. In the described reinforcement learning scenarios above, such as self-driving, competitive gaming, and autonomous robots, an agent is typically trained from scratch in a simulated environment. This policy, trained in the simulation, is then transferred to the real world.
For example, consider the case of autonomous robots. A realistic virtual environment, like those created with video game engines, is used, with an accurate model of the robot and the various motors involved in its control [7]. The policy can then control the motors of the simulated robot to try and attain some reward or goal. Transferring a policy from a simulated space to the real world is easier when the simulation is similar to the real world, emphasizing the quality of the simulated environment to decrease the domain gap [64].
Constructing an environment requires a deep understanding of how actions cause the environment to respond. In some settings, such as competitive chess playing, this is trivial: strict rules define how the pieces move and there is no stochasticity that affects the outcome of each action. In the case of self-driving, the actions and how the environment responds have a measure of stochasticity. While turning the wheel to the left typically turns the vehicle to the left, features of the environment, e.g. a patch of ice on the road, can affect the car’s trajectory in a unintended manner.
In our setting, the effects of a policy’s actions on the simulated environment are not easily defined. For example, similar actions performed by the policy may vary in their outcome due to differences between students. Even when asking two different students the exact same question, their responses will most likely differ. The environment, therefore, must use the collected data to model many potential outcomes for actions taken.
2.1 Education and Reinforcement Learning
Reinforcement learning in education has been a topic of exploration since the early 1960s [24], specifically for the sequencing of instructional activities. Various approaches have been built on this concept over the years [3, 33, 11]. A survey performed by Doroudi et al. found that 21 of 36 studies of RL-sequenced instructional policies determined that the RL policy outperformed baseline policies [15].
Singla et al. present a recent survey of the use of RL in education [56], which identifies five main research directions of RL in education. Singla found RL was used for: personalizing curriculums [15, 48], personalizing hints/scaffolding/ quizzing [2, 62, 45], A/B testing educational methods [34, 63, 49], modeling human students [22, 60, 26], and content generation [28, 27, 20]. Our work combines personalizing constructive feedback and modeling human students. In our setting, where we attempt to maximize collaboration between students, we model the students’ interactions regarding the feedback and hints provided.
2.2 Emma: The Teachable Robot
Our study context involves Emma, a humanoid NAO robot who interacts with a pair of students tasked to solve multiple ratio word problems, using natural language and basic gesture. NAO robots are commonly used and have been effective in social robot student learning settings [25]. The students work together to solve the problem and teach the solution to Emma. This collaboration has two benefits. First, we can obtain more data regarding student thinking, as they must vocalize more between themselves, compared to when working alone. Second, there are known benefits for student collaboration for improving student learning [8, 14].
During a study session, each question is shown to the pair of students, who need to solve the problem and then describe to Emma how to calculate the solution. The problems require multiple steps to solve, and the students need to convey each step to Emma. If one of the steps is wrong, Emma is designed to either ask a question to guide the students in the right direction or make a statement regarding the students’ response. An example interaction between students and Emma is shown below:
- 1.
- Emma: So I know that I need 66 hours worth of batteries and I know how much time I need for one battery.
- 2.
- Student B: So we can tell her 66 hours divided by 3 and three quarter hours.
- 3.
- Student A: Yeah, that’s right
- 4.
- Student B: So you’re going to divide 66 hours by 3 and three quarter hours.
- 5.
- Emma: Since we need to figure out what times 3 and three quarters is 66. So then 66 divided by 3 and three quarters is 17.6 Is that it?
- 6.
- Student B: Yes, that is correct.
- 7.
- Emma: I need 18 batteries because I need more than 17. I will put the answer as 18.
Students use an in-house web interface to see the math problem that the robot was solving, which provides controls to advance to the next step, a button to “push to speak” with the robot, and to see what the robot most recently said (as a backup to hearing it over the video chat service). The video feeds from each session (group) were recorded, along with the audio from each participant. The audio feeds for each participant were transcribed using IBM Watson’s Speech-to-Text system, with word timings maintained.
Our work follows two theoretical frameworks for identifying productive collaboration. First, the interactive-constructive-active-passive (ICAP) framework of cognitive engagement [10] hypothesizes that students collaborate best when actively interacting, taking turns to contribute constructively to the task at hand. In our environment, this would involve the students both working to teach Emma, participating relatively equally and engaging in dialogue with each other rather than pursuing independent parallel work. Second, we draw on the Interactive Alignment Model (IAM), which postulates that in order for two collaborators to align their understanding, they must align their communication [19]. One indication of this alignment is lexical entrainment, which is indeed related to student success in group learning settings [18]. Lexical entrainment measures the similarity between the language used by speakers in a group over time [6], and might be a sign of students converging to a shared mental model [18], which can lead to successful group performance [61]. We are interested in exploring both balance of participation and lexical entrainment as rewards in an RL environment.
2.3 Data Corpus
Due to the COVID-19 pandemic, sessions were held using an online video-chat service to connect the students with Emma. For our pilot studies, we collected data from twenty-eight undergraduate students who interacted with the robot in groups of two (i.e., 14 dyadic sessions; 11% Male, 89% Female; 32% Asian, 14% Black, 46% White, 7% no response; Mean age = 19.4 years, SD = 1.19)2. Each session lasted approximately 30 minutes.
In addition, students were individually tested and surveyed before and after collaboratively interacting with the robot. These assessments were used to determine pre-existing (i.e., pre-collaboration) factors that may impact mid-collaboration interactions and participation and post collaboration learning outcomes. The pre-collaboration measures included: motivation (i.e., interest, utility, efficacy, attainment, and cost), goal orientations (i.e., mastery approach, performance approach, performance-avoidance), attitudes towards robots and collaboration (i.e., work quality, peer support, interdependence), affinity for technology, and prior knowledge (i.e., pretest on ratios). The post-collaboration measures included ratings of rapport with their partner and Emma (i.e., general, positivity, or attentiveness), perceptions of Emma (i.e., anthropomorphism, likeability, animacy, and intelligence) [36, 35], and posttest scores (i.e., counterbalanced with pretest). Given the need to consider the group as the unit of analysis, we used the dyads’ average measures for our analyses, with higher averages representing a larger presence of each construct. In total, 27 metrics were collected from the surveys and assessments. This study was approved by the Institutional Review Board.
3. METHODOLOGY
We construct our simulated environment using real-world data collected from interactions with real students. The environment models the conversational interactions between all participants and uses probabilistic methods to capture the various sources of stochasticity. This allows us to model potential outcomes that could occur when Emma interacts with the students, even when such an interaction was not captured in the pilot study. We then train a set of three RL algorithms using the environment and compare the results of each algorithm with a series of baselines.
3.1 Data and Setup
Building an end-to-end RL environment is highly task-specific but can be generally simplified into two steps. We first extract the data gathered during the student interaction sessions. Next, we use the extracted data to model student interaction and observations in the environment in conjunction with various probabilistic sequence modeling techniques. This process involves identifying reward metrics and modeling how the environment responds to stimuli.
3.1.1 Student Participation Metrics
Our data-driven simulation uses various metrics captured during the data collection studies. Specifically, we capture the change in student participation metrics after Emma performs an action. We observe how these metrics change throughout the study as the students interact with each other and the robot. We use metrics that approximate the balance of interactive participation (following the ICAP framework) and lexical entrainment between the students. For our environment, we use Measure of Participation and Word Co-Occurrence metrics, respectively.
The text transcripts were tokenized at the sentence level using NLTK [5]. The Measure of Participation and Word Co-Occurrence were calculated as shown below, and associated with each sentence. This methodology allows us to estimate the balance of participation and lexical entrainment at intermediate points of the session.
Measure of Participation (MoP) MoP indicates the balance of group participation as proposed by Paletz and Schunn [43]. MoP computes the average level of involvement in the group, scaled between 0 (equal) and 1 (dominated) participation. MoP is defined in Equation 1, where is the average number of people during the session, is the max number of people present (always 2 in our setting), is the total number of utterances said in the session, is the number of people present on utterance K (always 2), is the index representing a student, and is the number of utterances where person is present.
For example, given two utterances and one participant speaks during each, MOP=4*(|1/2-1/2|+|-1/2+1/2|)/[2*(2+2)] =0. If only the first participant speaks during each utterance, MOP=4*(|1/2+1/2|+|-1/2-1/2|)/[2*(2+2)]=4*2/8=1.
This metric is invariant to changes in group size and supports groups of different sizes. In our RL environment, since the agent’s goal is to maximize the reward, we use for the feedback. This, in turn, rewards the agent for achieving equal participation.
Word Co-Occurrence (WCO) WCO provides a simple estimate of lexical entrainment. WCO is defined as the number of lemmas common between both participants. Lemmatization was performed using WordNet in NLTK. To get WCO in the same range as MoP, the value is normalized between and by dividing by the number of unique words said in the session. The size of the shared set of words increases only if both participants are contributing and talking about similar material.
3.2 Overview of the RL Environment
A reinforcement learning environment requires four essential components. The first is the set of potential actions that the agent can take at each step. The second is the set of states that the environment can take . The last is the set of rewards that the agent will be attempting to maximize.
The first step to building an environment is defining each of the required components of the environment and at what level of abstraction these components will be represented. We define how the environment responds when the robot interacts with it, the information provided by the environment to the robot, and the options the robot can take at each step.
3.2.1 States
The environment state is used to describe to the RL policy what is happening at a specific point in time. In this case, we model the environment state as a representation of the sentence said directly to Emma by one of the students - this is what Emma observes and uses to select her next action. For example, a student may tell Emma, “If you use 3/4 of your battery in 1 hour, you multiply that by 3 to figure out how much you use in 3 hours”.
3.2.2 Actions
In the case of determining the action space of the environment, we look at what Emma was capable of during the data collection sessions. As a proof of concept for our reinforcement learning approach, we simplify the action space to include the two general responses – questions and statements. For example, one response from Emma is this question-based reply: “So if I have forty-five hot dogs and I now know how much it costs for one, can I figure out how much it costs for forty-five hot dogs by multiplying?”. For the statement-based reply for the same problem, she says, “With the unit rate, I know it costs two dollars and fifteen cents for each hot dog. I don’t remember what I am supposed to do with that, though.” As we can see, while the responses convey similar information about the problem, they could potentially invoke very different responses in the student participants.
3.2.3 State Transitions
In addition to defining the states and actions of the environment, we need to define how the actions cause the states to transition from one to another. Our state transitions describe how the students react to Emma’s responses. Between Emma’s actions, there are a series of interactions between the students, where they decide what to say to Emma or work on the problem solution. We model the progression of these inter-student interactions probabilistically to describe how the students’ conversations lead to different interactions with Emma.
3.2.4 Reward
The purpose of the reward is to coerce the policy towards performing the actions needed to achieve the required outcome. There are broadly two ways to reward the agent: at constant intervals throughout a session or once at the end, but the latter sparse option is more complex than frequent rewards [21]. Our student participation metrics (Sec. 3.1.1), derived from learning theory hypotheses, can be calculated at intermediate points during the session. To keep the environment simple, we give an intermediate reward after each of the robot’s actions. The value of the reward is the sum of the student participation metrics associated with the current state (MoP + WCO), as observed during data collection.
3.3 Simulation
Now that we have presented a high-level view of the environment that was designed, we will delve into the technical details about how it is implemented. In the sections below, we highlight three difficulties in implementing a data-driven environment from previously collected data. First, the conversations between the students can vary significantly but need to be accurately modeled. Second, with data collection limits, we must handle missing information when simulating the outcome of actions. Third, the simulation must provide a reward to provide feedback for the selected actions.
3.3.1 Simulation Design
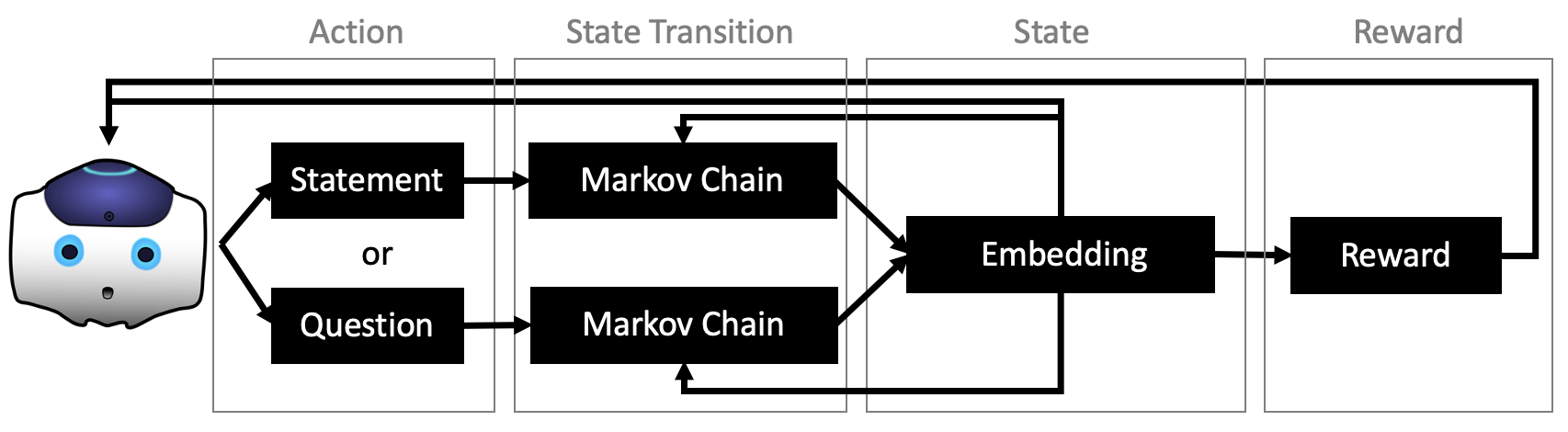
An overview of the environment is shown in Figure 1. Emma is capable of two responses, to either reply with a question or a statement. Each action has a unique Markov chain, which generates a sequence of simulated interactions between students. The generation of the simulated interactions is dependent on the current state of the environment and is used to generate the subsequent state. This subsequent state is associated with a reward for Emma.
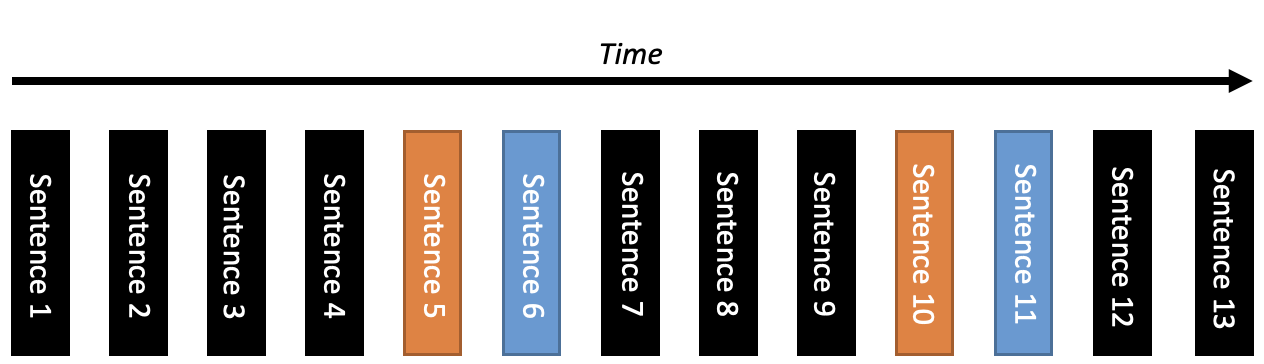
In Figure 2, we depict an example of the structure of the collected data, with time represented on the x-axis. Here, the black blocks signify a sentence said by a student to another student, the orange blocks represent a sentence said to Emma, and the blue blocks indicate Emma’s response to the students. The students say four sentences among themselves before one student says a sentence that is an input to Emma. The 6th block is the reply Emma chooses for the students. The students talk between themselves for three sentences before interacting with Emma again. Emma responds, the students continue talking, and the cycle repeats.
We can see that the interactions between the students have a structured turn-taking nature, which follows a repeated pattern: 1. students converse between themselves, 2. students provide an input to Emma, 3. Emma replies to the student’s input. Using this general structure of interaction, we can define the necessary portions of the environment. The state of the environment, as observed by the RL policy, is the sentence that is said directly to Emma. The actions in the environment are the replies from Emma to the students. The rewards of the environment are the changes in the levels of the Measure of Participation and Word Co-Occurrence scores that occur as the students discuss. The rewards are provided at the end of each sentence. The state transitions occur due to Emma’s responses (actions) to the students - this invokes conversation between the students, resulting in a specific response from the student (state).
3.3.2 State Space ()
The first step in building the environment is setting a level of abstraction to represent the states, . This step is important for modeling the environment input to the RL agent and is necessary in describing how the environment transitions from one state to the next. The interactions between the students and Emma can be modeled using the input sentence tokens, which are the orange blocks in Figure 2.
The tokens are encoded using Google’s pre-trained Universal Sentence Encoder [9]. The Universal Sentence Encoder provides embedding vectors of each token, for the tokens said between the students and the tokens said as input to Emma. Embedding vectors are high-dimensional representations in a semantic space. The embeddings of semantically similar tokens will have a higher cosine similarity score than semantically different tokens.
Let be a sentence in the set of sentence tokens said as input to Emma, collected during data collection, and converts a token to a 512-dimensional embedding with the Universal Sentence Encoder. A state in the environment is defined as , where .
3.3.3 Action Space ()
In Figure 2, Emma’s “actions” are her natural language replies shown as the blue blocks. For simplicity, Emma has the same set of actions that can be taken at each step. The replies to the students are roughly split into two categories: question-based replies and statement-based replies. An action at timestep has an indicator, , to describe the type of action taken. can be one of , i.e. Emma can reply with a question or a statement .
3.3.4 State Transitions
One vital mechanism for an environment is the state-action transition. The state-action transition defines for some state and action at time step , the next state emitted by the environment, at time step . Referring again to Figure 2 (black-colored sentence tokens), we see that an action is followed by dialogue between students, which takes place when transitioning between states.
We model this state-action transition using the Markov chain, a probabilistic sequence model. We choose to use the Markov chain for this simulation due to its simplicity and ability to model time-series data. A Markov chain is a simple model where the probability of the nth event at time , is conditioned and only dependent on the previous event . Here, each event is a sentence uttered by a student, and the chain represents the transitions of the conversation had between the students before they converse with Emma.
To build the Markov chain, we must simplify the events from the continuous space (sentence embeddings) to a countable space. With semantically similar sentences existing close together in the embedding space, unsupervised clustering methods allow for an intelligent way to represent the sentence tokens in a countable space. The embeddings for the transitional sentences are assigned to clusters in an unsupervised manner via KMeans clustering. Each sentence is assigned and represented by a cluster via this method. The set of clusters is the countable space for the Markov chain. We denote here a function which for event embedding , returns the cluster identifier of each embedding, . For simplicity, we extend to support operations on a sequence of events, which it converts to a sequence of cluster identifiers in the same order.
The state-action transition sequences collected from the pilot study are used to build the chains. For each state-action transition sequence, we store the action , the starting state , the transitional sequence of sentence embeddings and ensuing state . The transitional sentences, and ensuing state are combined as a sequence of embeddings . This sequence of embeddings is then transformed to be represented in terms of each sentence’s cluster identifier, . We also define another function, , which randomly samples and returns a sentence (its embedding) from cluster . These sequences of cluster identifiers are used to build a Markov chain. A separate Markov chain is built for each action to separate the state transitions of the two types of actions. These action-specific Markov chains are and , respectively.
State transitions are modeled using a conditional generation of the Markov chains. Sequences generated by Markov chains are typically initialized randomly by selecting a random event as the starting point. Conditional generation involves selecting a specific event as a starting point, which affects the subsequent generation of events in a cascading manner. This conditioning ensures the actions selected by Emma in the virtual environment affect the following simulated interactions between the students. To describe conditional generation, we provide the example , to represent the conditional generation of the next state using the question Markov chain. The output of , is a sequence of cluster identifiers , that starts with cluster identifier .
Mappings, , are extracted from the recorded state-action transitions, to be used for the data-driven conditional generation. For an observed state with action , the Markov chain conditionally generates with starting point , and ends with some cluster identifier . For example, we generate the following sequence of events, , and use the last event to obtain our sampled cluster identifier, . This cluster is used to sample next state, . We denote the set of recorded state-action transition mappings .
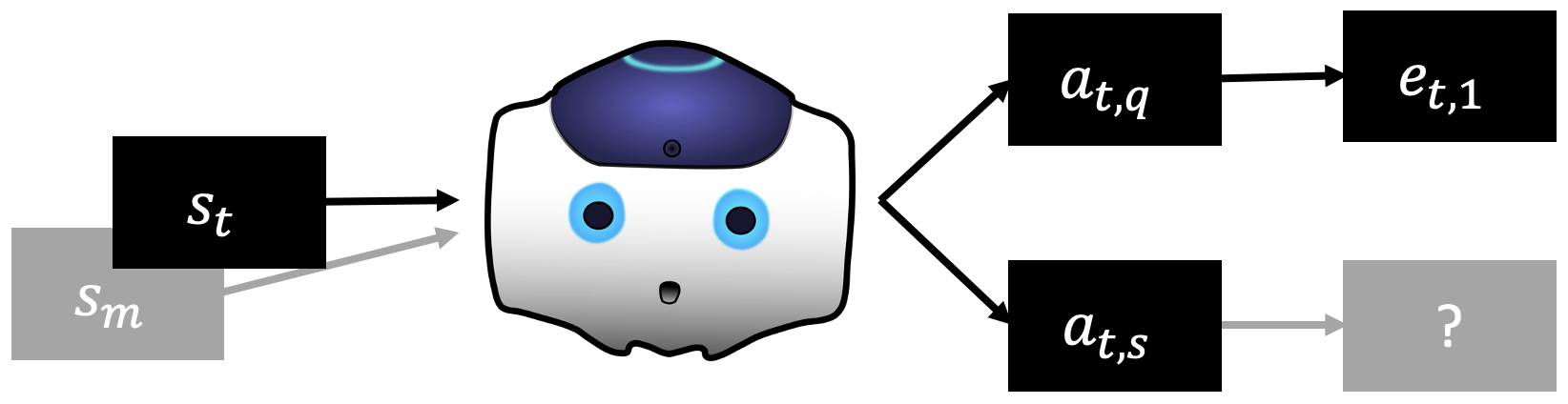
State-Action Map Substitution The data-driven mappings, , are a straightforward way to conditionally generate the next state, for some observed set of state and action, . However, consider the example in Figure 3. During data collection, we observed and recorded the mapping , shown in the top row. However, we may, during the simulation, want to test what happens for the state-action set , for which no recorded mapping exists. With no existing mapping, we need to find a substitute - a recorded mapping with a state that is similar to , that instead contains action .
We propose to find a substitute mapping by filtering the set of all recorded state-action transition mappings . Within , we filter and keep recorded mappings that contain the desired action, in this example. For each mapping in the filtered set, we calculate the cosine similarity score between the current state of the environment, and the state stored in the mapping. This similarity score is used to assign a probability for being selected as the substitute mapping to each mapping in the filtered set. The probabilities are proportional to the similarity score so that the most similar states have the highest probability of being selected. The filtered set is then sampled using the probabilities to find a new mapping, with a similar state , the selected action , and a new substitute event for conditional generation .
3.3.5 Reward ()
The formulation of the environment reward is simple since each entry in the Markov chain has an associated change in WCO and MoP that was observed during data collection. Therefore, during a state transition, we aggregate the WCO and MoP across the sequence generated by the Markov chain while generating the next step. The sum of the rewards over the chain is the reward provided for the action.
As a reminder, each entry in the chain is a specific cluster identifier in which various sentences reside. We use the cluster’s mean reward (using all the sentences in the cluster). As an example, if Emma selects a question as her action, we sample the Markov chain, , to generate the next state . This generates the chain: where . Each entry, , in the chain has an associated reward (WCO + MoP). Let be the average reward for cluster , where . To get an action’s full reward, we compute the sum of the associated rewards along the sampled chain .
Time Constraints To ensure that the environment does not provide rewards that bias policies towards selecting actions that have longer Markov chains, we add a time limit to how long an environment can run. The sentences said during data collection are timestamped, which describes how much time was required to say each sentence. Throughout the simulation, a timer is kept, and if a sentence is sampled by the Markov chain, the timer increments by the amount of time required to say the sentence, using the word timings extracted from the automated Speech-to-Text system. The time limit is a 30-minute cutoff, which mirrors the cap to session length that was in place during data collection. Any reward obtained after the cutoff is excluded.
3.3.6 Additional Implementation Details
Random Student Initialization The environment is designed to create a policy that is capable of handling different types of learners, different styles of student participation, and different levels of student interaction with Emma. To emulate this, during the environment initialization, Emma is blindly assigned to a random student group (one of the 14 from the pilot study); the policy is not provided information about which group was selected. Emma interacts with a version of the environment that uses state, state transition, and reward parameters collected from only the selected student group during that session. For subsequent sessions in the simulation, the student group is blindly and randomly re-assigned, ensuring that the learned policy can generalize to multiple types of students. These parameters differ per group, meaning the environments respond quite differently, depending on the current student group being represented.
Environment Tuning The first step, before training the Reinforcement Learning policy, is to make sure that the environment works as intended given the assumptions we used to model the states, actions, rewards, and state transitions. To do so, we built a deterministic policy for each group, which selects actions exactly as were selected by Emma in the pilot study - we call this deterministic policy the mirror policy. To be specific, in the simulation, she only picks actions that have an observed state-action transition, so no action substitution is used. While there is some stochasticity in the environment that comes from sampling the Markov chains, the environment should respond, on average, similarly to the outcomes that were observed during the pilot study.
To calculate the environment similarity, we directly compare the mirror policy’s action distribution and the action distribution of the studies during data collection. This comparison is made by comparing the ratio of mirror policy’s action distribution and the study action distribution, using mean squared error (MSE). We call this metric the action distribution difference. A low action distribution difference indicates that the environment reacts as expected.
Policy Tuning We tested three standard methods for reinforcement learning, Deep Q-Network (DQN), Proximal Policy Optimization (PPO), and Advantage-Actor Critic (A2C). DQN is a Q-learning method where a neural network learns the value of actions for a particular state. PPO is a policy-gradient method, which estimates the policy gradients directly with respect to the reward. A2C is an actor-critic method, where the critic learns the value of a state, and an actor to learn how to select actions. These policies are implemented using the Stable Baselines package [50].
4. RESULTS
Comparing RL Policy to Observed Decisions Once we identify the best RL policy, we compare the actions and rewards it achieves to those of the deterministic policy used during data collection, as a sanity check for our environment.
Comparing RL Policy to Random Baseline To see the performance of the learned policy against an unbiased policy, we compare the former against a random policy, which selects actions with equal probability. Consistently outperforming a random policy demonstrates that the learned policy learned to navigate the environment and correctly select actions.
Group Equality The amplitude of a policy’s reward in the environment is not the only goal for a successful policy. On top of maximizing the reward, we look to ensure group equality, i.e. positive reward across all groups - to verify that the learned policy helps different types of students.
Correlations of RL Policy Gains with Student Survey and Test Metrics The survey and assessment measures were not used in the environment design or parameters but could impact, or be impacted by, our RL metrics. Thus, we used the Pearson correlation coefficient to determine which dyadic factors (i.e., from the average survey and assessments metrics) were most highly associated with our RL Policy’s improvement in rewards. Doing so provides insight into how pre-existing factors connect to rewards during interactions with the robot and how these interactions connect to post-collaboration perceptions and assessments.
4.1 Evaluating the Environment
The mirror policy is used to tune the environment, and ensure that the environment works as expected. The number of clusters used for the sentence representation affects the level of stochasticity in the environment. This stochasticity is present in the language generated via the Markov Chains. An insufficient amount of clusters can result in a loss of the structure in the environment. With less clusters, the language generation becomes more random, and fails to capture the information from the pilot study. An excessive amount of clusters can cause the environment to respond only as was observed during the pilot study, generating nearly-identical language to what was observed.
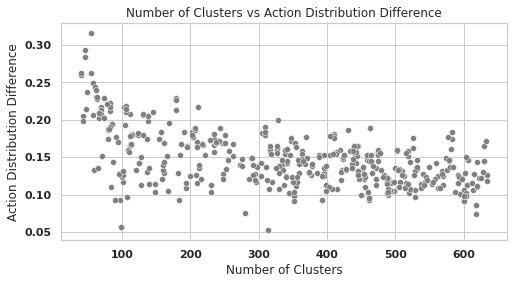
To determine the correct number of clusters, the mirror policy’s action distribution was evaluated while varying the number of clusters compared to the real distribution, as shown in Figure 4. Under 100 clusters, we see a large difference in how the environment responds to the mirror policy’s actions compared to the observed distribution. However, as we increase , we see a decrease in the difference, with little improvement when . For that reason, we set for all further experiments to ensure that there is some variability in the environment without deviating from what was observed in data collection.
In Figure 5, we display the action distribution of the mirror policy in the simulated environment compared to the observed real-world data. We can see the mirror policy acts quite similarly to what was observed in the real world – differences in actions come from the various sources of stochasticity in the environment.
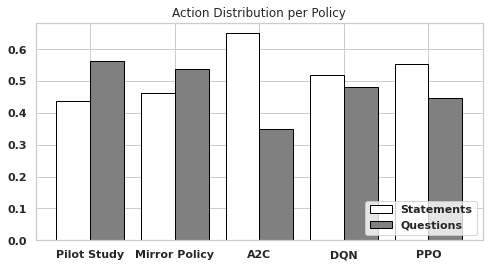
4.2 Evaluating the Policy
Questions are used more often than statements in both the pilot study and the mirror policy, but all RL policies flip the action distribution around - preferring statements over questions, indicating that there may be deficiencies in the deterministic policy used for the pilot study.
Tuning and validating the policy were done via two types of cross-validation. We tested the environment using traditional 5-fold cross-validation, where the 14 groups are separated into five subsets or folds, and each fold is used as a testing set. This methodology models the scenario where Emma is trained then evaluated with multiple unseen groups of students. This setting aims to demonstrate that learned policies provide benefit to more than one group.
To further validate policies learned in the environment, we also test leave-one-out cross-validation, where each student group is used as a testing set. In this scenario, we model the event where Emma is trained in a simulated environment, then evaluated with a single unseen group of students. This setting is to demonstrate that learned policies provide benefit to all groups.
We compared various learning rates in both scenarios and three RL policy optimization algorithms, PPO, DQN, and A2C. In total, 7087 different policies were trained and tested. Cross-validation takes 75W of power and runs for approximately 35 minutes. Training was performed on 2 Nvidia GTX 1080ti ($699 MSRP each). Data collection was performed with one NAO Robot ($12990 MSRP).
4.2.1 RL Method Performance Differences
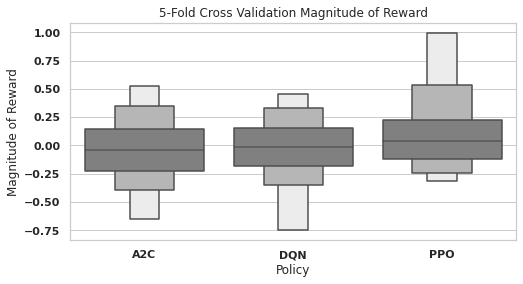
We refer to the difference in reward between an RL method and the mirror policy baseline as the Magnitude of Reward. In 5-fold cross-validation (Figure 6), the mirror policy outperformed the median A2C and DQN policies, as demonstrated by the slightly negative magnitude of reward. A2C’s magnitude of reward distribution is roughly normal, while DQN’s is negatively skewed. The median PPO policy outperformed the mirror policy, with a positive magnitude of reward. Furthermore, the PPO magnitude of reward distribution is positively skewed. PPO has an average magnitude of reward of , while A2C and DQN both have an average magnitude of reward of and , respectively.
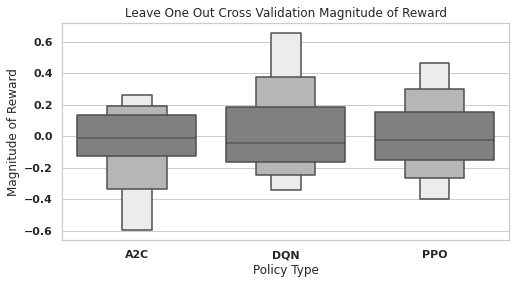
In leave-one-out cross-validation (Figure 7), we see that the median magnitude of rewards for all RL policies is slightly negative. However, while A2C is negatively skewed, DQN is positively skewed - the average DQN magnitude of reward is slightly positive. The mean rewards of A2C, DQN, and PPO are , and , respectively. In both settings a higher learning rate resulted in an increase in the policy’s reward on average.
A2C under-performed the mirror policy in both cross-validation settings, indicating that it does not work well in this environment. While DQN outperformed PPO in leave-one-out cross-validation, it under-performed the mirror policy in 5-fold cross-validation, indicating a lack of stability between settings. PPO outperformed the mirror policy in both settings, demonstrating positive and stable performance.
4.2.2 Gains for Individual Groups
The magnitude of reward of the policy is not the only goal of using an RL policy. We also aim to help improve groups that performed poorly during the diagnostic testing so that there is equal performance and improvement among all groups. Gains among low-performing groups mean that the policy may potentially aid students who learn in non-standard ways.
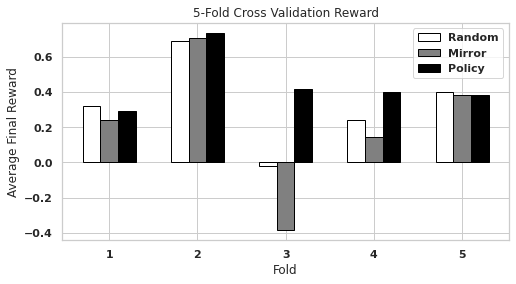
Figure 8 shows that the learned PPO RL policies achieve a consistent and positive average final reward in cross-validation among all folds. Here, the mirror policy achieves very inconsistent results among folds and a negative reward for Fold 3. The random-action baseline outperforms the mirror policy here but achieves approximately reward for Fold 3.
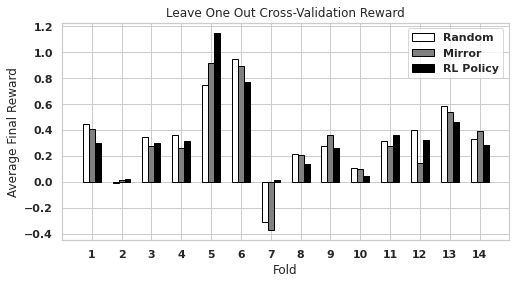
We see similar trends in leave-one-out cross-validation (Figure 9) but slightly more variation. Here, the PPO RL policies again achieve a positive reward, while the mirror policy and random-action baseline do not. The mirror policy and random baseline both achieved a negative reward for Fold 7, and the random baseline achieved a slightly negative reward for Fold 2. We note that Fold 2 generally did not respond significantly to any method, but the PPO RL policies achieved the highest average reward.
4.3 Correlations with Diagnostic Metrics
To determine the connections of our simulated environment to different dyadic factors, we calculated correlations between the Magnitude of Reward and metrics obtained by the questionnaire and assessments administered to students. These correlations may reveal which students are most positively affected by the boost in MoP and WCO that the learned policies can achieve in the simulated environment. We select the three diagnostic metrics with the highest Pearson correlation coefficients (in amplitude).
First, the large positive Pearson correlation between the dyads’ average self-reported values for quality of work in groups and the Magnitude of Reward suggests that students who more highly value the quality of work in collaborative settings may have benefited more from the actions of the learned policies. We would expect to see this correlation, given the overlapping nature of the group-work quality construct and key components of Magnitude of Reward (i.e., balance of participation and entrainment).
Furthermore, the high negative correlation between the dyads’ average pretest scores and the Magnitude of Reward of the policy may suggest that the groups with lower prior knowledge before the activity would likely have benefited more (i.e., better entrainment and balance of participation) from a policy that was trained in the reinforcement learning environment. Similarly, the high correlation between Magnitude of Reward and the dyadic-average understanding of ratios at posttest implies that the groups who performed worse, on average, than their counterparts could have been benefited by the improved balance of participation and word co-occurrence from the reinforcement learning policies.
5. DISCUSSION AND CONCLUSION
Our tests show that our environment exhibits a similar behavior under the mirror policy as was observed during the pilot study, in terms of action distribution (Figure 5). Notably, the policies learned in the environment differ significantly from the pilot study and the mirror policy, heavily favoring statements over questions, opposite to the rule-based approach used for the mirror policy. One explanation is that a question occasionally resulted in a direct response from the student who originally spoke to Emma. We observed that statements more often resulted in the students reconvening and then discussing how to reply to Emma.
This assignment of actions may have its merits, based on its improvements in both the amplitude and consistency of environment reward. In both forms of cross-validation, the policies trained with PPO outperform the mirror policy. We note that other RL methods had inconsistent performance across different types of cross-validation. In the Proximal Policy Optimization algorithm paper [52], the author finds a improvement in performance and sample efficiency using PPO over DQN and A2C. In our setting, we are limited in our number of data-driven samples, and therefore PPO’s strong performance may be from this data efficiency.
When looking at the results of the individual folds for both forms of cross-validation, we see that the PPO RL policies consistently achieve a net positive reward. In 5-fold cross-validation, RL’s rewards are consistent across folds, while the mirror policy and random baselines were inconsistent and even resulted in a significant decrease in one fold’s average reward. This trend extends to leave-one-out cross-validation, where the PPO RL policies again achieved a positive reward on all folds. From our testing, we believe that the PPO RL policies may benefit all students and demonstrate performance equity among groups.
These findings are further highlighted by the connections between the learned policies’ Magnitude of Reward and the metrics obtained by the questionnaire and students’ diagnostic tests. The Pearson correlations may reveal which students are most positively affected by the additional MoP and WCO that the learned policies can achieve in the simulated environment. The actions of the learned policies may help the most for students who care highly about their quality of work in a group setting and may provide the most benefit for underperforming students. Further empirical investigation into these links might reveal new understanding of how interventions under the ICAP and IAM frameworks interact with individual differences to improve collaboration.
However, the policies trained in this environment have not yet been validated in a real-world setting with students. Additionally, the pilot study was performed using a hand-crafted and deterministic script for interacting with the students. The data collected by the script’s actions may have biases, which could affect the accuracy of the environment. Furthermore, the pilot study data collection was performed with undergraduate school students, held virtually. We aim to test this system in-person and with middle-school students. We expect some of our findings in this study may not carry over to this new setting. In addition, our investigation only looked at one modality. In the future, we aim to extend this work, adding additional actions such as verbal references towards particular students and adding physical gestures and gaze to the robot.
The framework presented here provides a hybrid approach for using RL in a robot-student setting, by building a environment from collected student interaction data. This environment can be adapted to any number of actions and students without requiring extensive training in the real world.
Acknowledgements: This work was supported by Grant No. 2024645 from the National Science Foundation, Grant No. 220020483 from the James S. McDonnell Foundation, and a University of Pittsburgh Learning Research and Development Center internal award. We would also like to thank Mike Diamond for his help with the pilot study.
6. REFERENCES
- F. Agostinelli, S. McAleer, A. Shmakov, and P. Baldi. Solving the Rubik’s cube with deep reinforcement learning and search. Nature Machine Intelligence, 1(8):356–363, Aug. 2019. Number: 8 Publisher: Nature Publishing Group.
- V. Aleven, E. A. McLaughlin, A. Glenn, and K. Koedinger. Instruction Based on Adaptive Learning Technologies. 2016.
- R. Atkinson. Optimizing the Learning of a Second-Language Vocabulary. Journal of Experimental Psychology, Vol.96(No 1):124–129, 1972.
- T. Belpaeme, J. Kennedy, A. Ramachandran, B. Scassellati, and F. Tanaka. Social robots for education: A review. Science Robotics, 2018.
- S. Bird, E. Klein, and E. Loper. Natural Language Processing with Python: Analyzing Text with the Natural Language Toolkit, 2009. original-date: 2009-09-07T10:53:58Z.
- S. Brennan. Lexical Entrainment In Spontaneous Dialog, 1996.
- G. Brockman, V. Cheung, L. Pettersson, J. Schneider, J. Schulman, J. Tang, and W. Zaremba. OpenAI Gym. June 2016.
- A. L. Brown and A. S. Palincsar. Guided, cooperative learning and individual knowledge acquisition. In Knowing, learning, and instruction: Essays in honor of Robert Glaser, pages 393–451. Lawrence Erlbaum Associates, Inc, Hillsdale, NJ, US, 1989.
- D. Cer, Y. Yang, S.-y. Kong, N. Hua, N. Limtiaco, R. St. John, N. Constant, M. Guajardo-Cespedes, S. Yuan, C. Tar, B. Strope, and R. Kurzweil. Universal Sentence Encoder for English. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing: System Demonstrations, pages 169–174, Brussels, Belgium, Nov. 2018. Association for Computational Linguistics.
- M. T. H. Chi and R. Wylie. The ICAP Framework: Linking Cognitive Engagement to Active Learning Outcomes. Educational Psychologist, 49(4):219–243, Oct. 2014.
- B. Clement, D. Roy, P.-Y. Oudeyer, and M. Lopes. Multi-Armed Bandits for Intelligent Tutoring Systems. Journal of Educational Data Mining, 7(2):20–48, June 2015. Number: 2.
- P. Dillenbourg. Chapter 1 (Introduction) What do you mean by ’collaborative learning’? Collaborative-learning: Cognitive and Computational Approaches, Vol. 1, Jan. 1999.
- P. Dillenbourg, S. Järvelä, and F. Fischer. The evolution of research on computer-supported collaborative learning. In Technology-enhanced learning, pages 3–19. Springer, 2009.
- W. Doise, G. Mugny, and A.-N. Perret-Clermont. Social interaction and the development of cognitive operations. European Journal of Social Psychology, 5(3):367–383, 1975. Place: US Publisher: John Wiley & Sons.
- S. Doroudi, V. Aleven, and E. Brunskill. Where’s the Reward?: A Review of Reinforcement Learning for Instructional Sequencing. International Journal of Artificial Intelligence in Education, 29(4):568–620, Dec. 2019.
- G. Dulac-Arnold, N. Levine, D. J. Mankowitz, J. Li, C. Paduraru, S. Gowal, and T. Hester. Challenges of real-world reinforcement learning: definitions, benchmarks and analysis. Machine Learning, 110(9):2419–2468, Sept. 2021.
- D. J. Foster, A. Krishnamurthy, D. Simchi-Levi, and Y. Xu. Offline Reinforcement Learning: Fundamental Barriers for Value Function Approximation. Nov. 2021.
- H. Friedberg, D. Litman, and S. B. F. Paletz. Lexical entrainment and success in student engineering groups. In 2012 IEEE Spoken Language Technology Workshop (SLT), pages 404–409, Miami, FL, USA, Dec. 2012. IEEE.
- S. Garrod and M. J. Pickering. Joint Action, Interactive Alignment, and Dialog. Topics in Cognitive Science, 1(2):292–304, 2009. _eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1111/j.1756-8765.2009.01020.x.
- L. Gisslen, A. Eakins, C. Gordillo, J. Bergdahl, and K. Tollmar. Adversarial Reinforcement Learning for Procedural Content Generation. In 2021 IEEE Conference on Games (CoG), pages 1–8, Copenhagen, Denmark, Aug. 2021. IEEE.
- J. Hare. Dealing with Sparse Rewards in Reinforcement Learning. arXiv:1910.09281 [cs, stat], Nov. 2019. arXiv: 1910.09281.
- L. Haug, S. Tschiatschek, and A. Singla. Teaching Inverse Reinforcement Learners via Features and Demonstrations. In Advances in Neural Information Processing Systems, volume 31. Curran Associates, Inc., 2018.
- D. Hood, S. Lemaignan, and P. Dillenbourg. When Children Teach a Robot to Write: An Autonomous Teachable Humanoid Which Uses Simulated Handwriting. In Proceedings of the Tenth Annual ACM/IEEE International Conference on Human-Robot Interaction, HRI ’15, pages 83–90, New York, NY, USA, Mar. 2015. Association for Computing Machinery.
- R. A. Howard. Dynamic programming and Markov processes. Technology Press of Massachusetts Institute of Technology, Cambridge, 1960.
- W. Johal. Research Trends in Social Robots for Learning. Current Robotics Reports, 1(3):75–83, Sept. 2020.
- P. Kamalaruban, R. Devidze, V. Cevher, and A. Singla. Interactive Teaching Algorithms for Inverse Reinforcement Learning. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, pages 2692–2700, Macao, China, Aug. 2019. International Joint Conferences on Artificial Intelligence Organization.
- B. Kartal, N. Sohre, and S. J. Guy. Data driven sokoban puzzle generation with monte carlo tree search. In Twelfth Artificial Intelligence and Interactive Digital Entertainment Conference, 2016.
- A. Khalifa, P. Bontrager, S. Earle, and J. Togelius. PCGRL: procedural content generation via reinforcement learning. In Proceedings of the Sixteenth AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment, AIIDE’20, pages 95–101. AAAI Press, Oct. 2020.
- B. R. Kiran, I. Sobh, V. Talpaert, P. Mannion, A. A. A. Sallab, S. Yogamani, and P. Pérez. Deep Reinforcement Learning for Autonomous Driving: A Survey. IEEE Transactions on Intelligent Transportation Systems, pages 1–18, 2021. Conference Name: IEEE Transactions on Intelligent Transportation Systems.
- E. Konijn and J. Hoorn. Robot tutor and pupils’ educational ability: Teaching the times tables. Computers & Education, 157:103970, July 2020.
- M. Lanz, R. Pieters, and R. Ghabcheloo. Learning environment for robotics education and industry-academia collaboration. Procedia Manufacturing, 31:79–84, Jan. 2019.
- J. Li. The benefit of being physically present: A survey of experimental works comparing copresent robots, telepresent robots and virtual agents. International Journal of Human-Computer Studies, 77:23–37, May 2015.
- R. V. Lindsey, M. C. Mozer, W. J. Huggins, and H. Pashler. Optimizing Instructional Policies. In Advances in Neural Information Processing Systems, volume 26. Curran Associates, Inc., 2013.
- C. Liu, R. Fang, and J. Chai. Towards Mediating Shared Perceptual Basis in Situated Dialogue. page 10.
- N. G. Lobczowski. Bridging gaps and moving forward: Building a new model for socioemotional formation and regulation. Educational Psychologist, 55(2):53–68, Apr. 2020. Publisher: Routledge _eprint: https://doi.org/10.1080/00461520.2019.1670064.
- N. Lubold, E. Walker, H. Pon-Barry, Y. Flores, and A. Ogan. Using Iterative Design to Create Efficacy-Building Social Experiences with a Teachable Robot. July 2018. Publisher: International Society of the Learning Sciences, Inc. [ISLS].
- S. Matsuzoe, H. Kuzuoka, and F. Tanaka. Learning English words with the aid of an autonomous care-receiving robot in a children’s group activity. The 23rd IEEE International Symposium on Robot and Human Interactive Communication, 2014.
- D. Miller, I. Nourbakhsh, and R. Siegwart. Robots for Education. In Springer Handbook of Robotics. Jan. 2008. Journal Abbreviation: Springer Handbook of Robotics.
- R. Mitnik, M. Nussbaum, and A. Soto. An autonomous educational mobile robot mediator. Autonomous Robots, 25:367, Nov. 2008.
- D. P. Newton and L. D. Newton. Humanoid Robots as Teachers and a Proposed Code of Practice. Frontiers in Education, 4, 2019.
- T. J. Nokes-Malach, J. E. Richey, and S. Gadgil. When is it better to learn together? Insights from research on collaborative learning. Educational Psychology Review, 27(4):645–656, 2015. Place: Germany Publisher: Springer.
- OpenAI, I. Akkaya, M. Andrychowicz, M. Chociej, M. Litwin, B. McGrew, A. Petron, A. Paino, M. Plappert, G. Powell, R. Ribas, J. Schneider, N. Tezak, J. Tworek, P. Welinder, L. Weng, Q. Yuan, W. Zaremba, and L. Zhang. Solving Rubik’s Cube with a Robot Hand. Oct. 2019.
- S. B. F. Paletz and C. D. Schunn. Assessing group-level participation in fluid teams: Testing a new metric. Behavior Research Methods, 43(2):522–536, June 2011.
- H. W. Park, I. Grover, S. Spaulding, L. Gomez, and C. Breazeal. A Model-Free Affective Reinforcement Learning Approach to Personalization of an Autonomous Social Robot Companion for Early Literacy Education. Proceedings of the AAAI Conference on Artificial Intelligence, 33:687–694, July 2019.
- T. Patikorn and N. T. Heffernan. Effectiveness of Crowd-Sourcing On-Demand Assistance from Teachers in Online Learning Platforms. In Proceedings of the Seventh ACM Conference on Learning @ Scale, L@S ’20, pages 115–124, New York, NY, USA, Aug. 2020. Association for Computing Machinery.
- A. Powers, S. Kiesler, S. Fussell, and C. Torrey. Comparing a computer agent with a humanoid robot. In Proceedings of the ACM/IEEE international conference on Human-robot interaction, pages 145–152, 2007.
- A. Rafferty, H. Ying, and J. Williams. Statistical Consequences of using Multi-armed Bandits to Conduct Adaptive Educational Experiments. Journal of Educational Data Mining, 11(1):47–79, June 2019. Number: 1.
- A. N. Rafferty, E. Brunskill, T. L. Griffiths, and P. Shafto. Faster Teaching via POMDP Planning. Cognitive Science, 40(6):1290–1332, Aug. 2016.
- A. N. Rafferty, H. Ying, and J. J. Williams. Bandit assignment for educational experiments: Benefits to students versus statistical power. In International Conference on Artificial Intelligence in Education, pages 286–290. Springer, 2018.
- A. Raffin, A. Hill, A. Gleave, A. Kanervisto, M. Ernestus, and N. Dormann. Stable-Baselines3: Reliable Reinforcement Learning Implementations.
- M. Saerbeck, T. Schut, C. Bartneck, and M. Janse. Expressive Robots in Education Varying the Degree of Social Supportive Behavior of a Robotic Tutor. volume 3, pages 1613–1622, Jan. 2010.
- J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov. Proximal Policy Optimization Algorithms. arXiv:1707.06347 [cs], Aug. 2017. arXiv: 1707.06347.
- A. Segal, Y. B. David, J. J. Williams, Y. Gal, and Y. Shalom. Combining Difficulty Ranking with Multi-Armed Bandits to Sequence Educational Content. In AIED, 2018.
- D. Silver, A. Huang, C. J. Maddison, A. Guez, L. Sifre, G. van den Driessche, J. Schrittwieser, I. Antonoglou, V. Panneershelvam, M. Lanctot, S. Dieleman, D. Grewe, J. Nham, N. Kalchbrenner, I. Sutskever, T. Lillicrap, M. Leach, K. Kavukcuoglu, T. Graepel, and D. Hassabis. Mastering the game of Go with deep neural networks and tree search. Nature, 529(7587):484–489, Jan. 2016. Number: 7587 Publisher: Nature Publishing Group.
- D. Silver, T. Hubert, J. Schrittwieser, I. Antonoglou, M. Lai, A. Guez, M. Lanctot, L. Sifre, D. Kumaran, T. Graepel, T. Lillicrap, K. Simonyan, and D. Hassabis. Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm. arXiv:1712.01815 [cs], Dec. 2017. arXiv: 1712.01815.
- A. Singla, A. N. Rafferty, G. Radanovic, and N. T. Heffernan. Reinforcement Learning for Education: Opportunities and Challenges. July 2021.
- A. Soller. Supporting Social Interaction in an Intelligent Collaborative Learning System. page 24.
- F. Tanaka, K. Isshiki, F. Takahashi, M. Uekusa, R. Sei, and K. Hayashi. Pepper learns together with children: Development of an educational application. 2015 IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), 2015.
- F. Tanaka and S. Matsuzoe. Children teach a care-receiving robot to promote their learning. HRI 2012, 2012.
- S. Tschiatschek, A. Ghosh, L. Haug, R. Devidze, and A. Singla. Learner-aware Teaching: Inverse Reinforcement Learning with Preferences and Constraints. In Advances in Neural Information Processing Systems, volume 32. Curran Associates, Inc., 2019.
- P. Van den Bossche, W. Gijselaers, M. Segers, G. Woltjer, and P. Kirschner. Team learning: building shared mental models. Instructional Science, 39(3):283–301, May 2011.
- J. J. Williams, J. Kim, A. Rafferty, S. Maldonado, K. Z. Gajos, W. S. Lasecki, and N. Heffernan. AXIS: Generating Explanations at Scale with Learnersourcing and Machine Learning. In Proceedings of the Third (2016) ACM Conference on Learning @ Scale, L@S ’16, pages 379–388, New York, NY, USA, Apr. 2016. Association for Computing Machinery.
- J. J. Williams, A. N. Rafferty, D. Tingley, A. Ang, W. S. Lasecki, and J. Kim. Enhancing Online Problems Through Instructor-Centered Tools for Randomized Experiments. In Proceedings of the 2018 CHI Conference on Human Factors in Computing Systems, pages 1–12. Association for Computing Machinery, New York, NY, USA, Apr. 2018.
- W. Zhao, J. P. Queralta, and T. Westerlund. Sim-to-Real Transfer in Deep Reinforcement Learning for Robotics: a Survey. In 2020 IEEE Symposium Series on Computational Intelligence (SSCI), pages 737–744, Dec. 2020.
1We note that contextual multi-armed bandits exist. However, they make the assumption that the actions picked have no effect on the environment (in this case, the students). We aim to model how the students’ behaviors change over time in response to the actions selected, and thus a contextual multi-armed bandit does not fit this problem.
2This data is part of a more extensive study that includes another condition in which individuals taught Emma. For the purposes of the current work, we focus on the dyads.
© 2022 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.