Neural Recall Network: A Neural Network Solution to Low Recall Problem in Regex-based Qualitative Coding

Cai, Zhiqiang; Marquart, Cody; Shaffer, David

doi:10.5281/zenodo.6853047

Zhiqiang Cai

University of

Wisconsin-Madison

zhiqiang.cai@wisc.edu

Cody Marquart

University of

Wisconsin-Madison

cody.marquart@wisc.edu

David W. Shaffer

University of

Wisconsin-Madison

dws@education.wisc.edu

ABSTRACT

Regular expression (regex) coding has advantages for text analysis. Humans are often able to quickly construct intelligible coding rules with high precision. That is, researchers can identify words and word patterns that correctly classify examples of a particular concept. And, it is often easy to identify false positives and improve the regex classifier so that the positive items are accurately captured. However, ensuring that a regex list is complete is a bigger challenge, because the concepts to be identified in data are often sparsely distributed, which makes it difficult to identify examples of false negatives. For this reason, regex-based classifiers suffer by having low recall. That is, it often misses items that should be classified as positive. In this paper, we provide a neural network solution to this problem by identifying a negative reversion set, in which false negative items occur much more frequently than in the data set as a whole. Thus, the regex classifier can be more quickly improved by adding missing regexes based on the false negatives found from the negative reversion set. This study used an existing data set collected from a simulation-based learning environment for which researchers had previously defined six codes and developed classifiers with validated regex lists. We randomly constructed incomplete (partial) regex lists and used neural network models to identify negative reversion sets in which the frequency of false negatives increased from a range of 3%-8% in the full data set to a range of 12%-52% in the negative reversion set. Based on this finding, we propose an interactive coding mechanism in which human-developed regex classifiers provide input for training machine learning algorithms and machine learning algorithms “smartly" select highly suspected false negative items for human to more quickly develop regex classifiers.

Keywords

Qualitative coding, Regex, text classification, neural network, recall, false negative density, negative reversion set

1. INTRODUCTION

Data mining, as Baker (2010) described, is the “field of discovering novel and potentially useful information from large amounts of data"[2]. A critical challenge in educational data mining (EDM) is extracting information from text data. In education settings, text data might come from team chats in collaborative learning environments[4], conversations between computer agents and human learners[12], team discussions, notes, essays and reports in virtual internship[8, 10], etc. Traditionally, qualitative coding is the first and most important step in analyzing text data[11, 6]. But as the size of data increases, manual coding becomes expensive and in some cases impossible. Machine learning (ML) based text classification methods thus play an important role in EDM.

1.1 Challenges in Automated Text Classification

Unsupervised ML, such as topic modeling, can automatically extract collections of words that might serve as topics in text data[3, 5]. Supervised ML, such as neural network text classification algorithms[13, 1] can be trained on a subset of manually coded data to predict coding for the remainder of the data. While such ML algorithms can quickly code large data sets, they have disadvantages that may lead to biased classification. For example, unsupervised ML algorithms often generate topics that occur with high frequency. Codes with relatively low frequency are often missed or vaguely represented[7]. Supervised ML algorithms, on the other hand, rely on human coded data, thus bias in training data will be inherited by machine learning models. Moreover, in some circumstances, the amount of human-coded data required to produce a reliable classifier using supervised ML methods can be prohibitive.

A third approach to automated coding is to use human-developed regular expressions (regex). Humans are often able to quickly construct intelligible coding rules with high precision. That is, researchers can identify words and word patterns that correctly classify examples of a particular concept. It is often easy to identify false positives and improve the regex classifier so that the positive items are accurately captured. However, ensuring that a regex list is complete is a bigger challenge. Because the concepts to be identified in data are often sparsely distributed, examples of false negatives are difficult to identify. This causes the low-recall problem in regex based classifiers. That is, the regex based classifiers often miss items that should be classified as positive.

In this paper, we explore the possibility of constructing an interactive coding mechanism in which human-developed regex classifiers provide input for training machine learning algorithms and machine learning algorithms provide cues for human to construct better unbiased regex classifiers.

2. OVERVIEW OF CODING PROCESSES

2.1 Manual Coding

Manual coding of text data is a complex process. Done well, it requires researchers to intensively read their data to discover and construct appropriate theories and develop codes that reflect those theoretical machinery [11, 16, 15]. Hand coding typically begins when text data is segmented into meaningful units, or items of data. Codes are then induced by sorting and interpreting observations item by item. A grounded coding process iterates through three coding phases: open coding, axial coding and selective coding. In open coding, a researcher goes through the data to identify preliminary concepts. The concepts are then compared and categorized in axial coding. Once a conceptual framework is established, the researcher focuses on a fixed set of codes in the selective coding phase and identifies which items each code occurs.

Key to the process of manual coding is identifying a precise definition for each code (usually accompanied by examples from the data). However, coding depends on how individual researchers understand each code: there are no rules specified that convert text into code in a deterministic way.

To address this concern, manual codes are validated, either through a process of social moderation (sometimes call dual coding) in which two or more coders come to agreement about each code for each observation in the data, or using some form of interrater reliability (IRR) that quantifies the rate of agreement between two coders.

Because manual coding requires that at least one human rater codes each item of the data and includes triangulation with at least one more human rater, the results from manual coding are considered the most accurate (compared with machine coding methods) and often serves as the gold standard orground truth to which other coding methods are compared.

Despite this advantage in terms of coding validity, manual coding can only be applied to data sets with relatively small size. Thus researchers turn to a variety of machine-based or machine-augmented coding techniques.

2.2 Keyword/Regex-based Coding

In the selective coding phase, when the size of a data set is too large for manual coding, researchers may turn to rule-based automatic coding [9]. Rules can be expressed in terms of text patterns described by regexes [14]. The simplest form of regex is a word, such as “teach". If this word is used to represent a code “Education", then the code “Education" occurs if and only if the text contains the string “teach". Thus, if a text contains the words “teacher",“teachers",“teaches" or “teaching", the code occurs, because “teach" is a sub-string of all these words. Regexes use a set of operators to specify complex patterns. The most frequently used operators include the pipe symbol “|", period “.", brackets “[]", and star “*". The pipe symbol “|" is used to compose alternative strings. For example, the regex “teach|student|school" matches a text containing any of the strings “teach", “student" or “school". A period “." indicates an arbitrary text character and brackets “[]" indicate a range of characters (e.g., [aeiouy] indicates any vowel in English), and the star “*" indicates an arbitrary repetition of the previous character. So the regex “my favorite vowel.*[aeiouy]" would code for the text “my favorite vowel" followed anywhere in the text string by a vowel. In this way, very complicated patterns can be represented by a single regex(see, e.g., https://www.regular-expressions.info/tutorial.html).

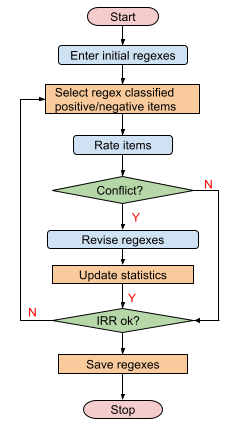
One powerful publicly available tool for regex-based coding is nCoder (https://app.n-coder.org/). nCoder uses an active machine learning approach to generating a regex-based classifier. Figure 1 shows the typical work flow of nCoder. A researcher starts from an initial regex list. nCoder uses that regex list to select a set of items to present to the researcher for rating. The set may proportionally include items that the regex list classified as positive or negative. nCoder then allows the researcher to rate the items and compares the researcher’s rating with the regex classification. When conflict occurs, the researcher may revise the regex list, change his or her rating, or leave the conflict unresolved. Inter-rater reliability (IRR) between the researcher and the regex classifier is then computed based on hypothesis testing. nCoder may present another set of items and repeat the rating-testing process. The process continues until the researcher and regex classifier reach a satisfactory level of agreement. The developed regexes are saved before the process terminates.[16].

The convergence of the above procedure depends on what data items are presented to the researcher. If a presented item is one that the human and regex classifier have agreement, no information is provided to the human to improve the regex list. Rather, it is the items where the two ratings conflict that help improve the regex list. This conflict may occur in two ways: one is false positive, in which the regex coded positive but the human coded negative; the other is false negative, in which the regex coded as negative but the human coded as positive.

Conceptually, we can partition a data set $D$ into two sets: a positive set $\tilde{P} \subset D$ of the items that would be coded as positive by current regex, and a negative set $Ñ = D - \tilde{P}$ that would be coded as negative by the regex list. False positive items are a subset of the positive set $\tilde{P}$ (because a false positive requires that the regex codes an item as positive); and false negative items are only in the negative set $Ñ$ (by similar reasoning).

Notice, however, when the frequency of a code is low (that is, there are few items that should be coded positive), the probability of sampling a false positive item from the positive set $\tilde{P}$ may be much higher than sampling a false negative item from the negative set $Ñ$ . Thus, it is more difficult for the active machine learning system to present users with false negatives, potentially allowing the regex development procedure to converge on a regex list with high precision but potentially lower recall (see the definition of precision and recall in section 3.4).

2.3 Machine learning-based Coding

Machine learning algorithms can be applied to both code discovery and selective coding. In the domain of code discovery, unsupervised machine learning algorithms, such as topic modeling, can automatically extract from a data set lists of related words that might potentially serve as codes. However, research shows that in most cases these word lists do not produce codes of interest to qualitative researchers without further refinement. But topic modeling can help identify missing codes by providing potential keywords for coding[5].

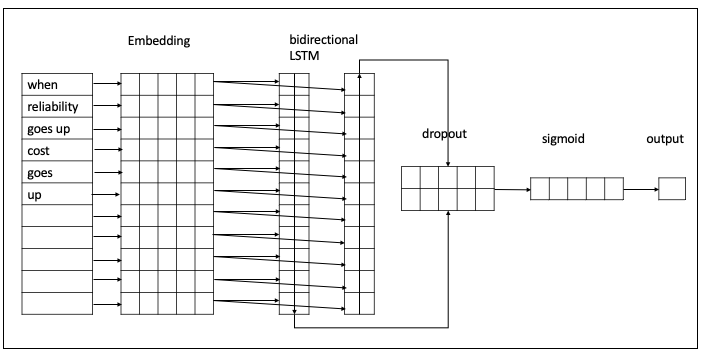
LSTM model for text classification — Figure 2: LSTM neural network model for text classification

One popular approach to using ML for selective coding is LSTM (Long Short Term Memory) neural network models. These models take as input a set of coded data items, and return an algorithm that can predict coding for the rest of the data. Figure 2 shows the model used in this study. A text data item enters from the input layer as an ordered word list. The embedding layer represents each unique word by a vector. The ordered vectors are input to a bidirectional LSTM layer that creates two vector representations of the input data line. The two vectors are merged into a single vector representation and 50% of the nodes are removed in the dropout layer to control over-fitting. The sigmoid layer converts the vector into a class probability output, which indicates for each item how likely the model thinks it should be coded positive. The probability values are then converted to a binary coding value using a cutoff threshold, say, 0.5. That is, when the probability is greater than 0.5, the item is coded as 1, otherwise 0. (Readers interested in more details about LSTM models can find more information in neural network publications such as [13].)

This kind of neural network model can represent very complicated patterns of words that serve as indicators for a code. However, it usually requires a large number of coded data items to train a neural network model to reach an acceptable accuracy; thus preparing the training data for the neural network model could be expensive. Moreover, like many other machine learning models, neural network models are a black box: the output is hard to interpret. When a neural network model flags the occurrence of a code in a data item, it can be hard (and often impossible) for a researcher to determine what specific evidence the algorithm used to make its decision. This makes it difficult for qualitative researchers to establish a theory with clear interpretation. In addition, it makes it difficult for researchers to understand potential biases in the codes and to warrant to end users that the result of the coding is fair.

2.4 Combining manual, regex and ML coding

Table 1 summarizes the advantages and disadvantages of the three coding methods we have discussed so far. In what follows, we construct and test an approach to coding that integrates these three methods together into a single process, in which we iterate between manual coding and regex coding to train a regex list. Then we use the data coded by the regex list to train the neural network model. The disagreements between regex coding and neural network coding are presented back to the researcher to further refine the regex coding. We will show that this combination helps solve the low recall problem in regex coding.

Table 1: Manual, Regex and ML Coding
	Manual	Regex	ML
Evidence	Explicit	Explicit	Implicit
Precision	High	High	Medium
Recall	High	Low	Medium
Coding size	Limited	Unlimited	Unlimited
Cost	High	Low	Medium

2.5 Approach

For a given data set $D$ and and a code $c$ , let a human rater’s classification be $D = P + N$ , where $P$ is the set of positive items (i.e., items in which code $c$ occurs) and $N$ is the set of negative items. The plus sign “ $+$ " denotes the union of two sets. In practice, the number of items in $P$ is usually much smaller than in $N$ (i.e., $| P | ≪ | N |$ ), because researchers are often interested in codes that do not occur with high frequency.

Of course, for a given item $x \in D$ , the coding algorithm cannot determine whether $x \in P$ or $x \in N$ without asking the human rater. Therefore, it is impossible for an algorithm to sample a new item from $P$ (or $N$ ) unless they have already been classified by the human rater. In this sense, the sets $P$ and $N$ are unsamplable, while the set $D$ is samplable. That is, a machine algorithm can choose an item $x \in D$ but it cannot choose with certainty whether sample $x \in P$ or $x \in N$ .

Consider a regex classifier that classifies the data set $D = \tilde{P} + Ñ$ . Since the machine knows the classification of all items in $D$ , the sets $\tilde{P}$ and $Ñ$ are samplable. The regex classifier is perfect if $P = \tilde{P}$ . In reality, however, this is rarely the case.

The data set $D$ thus can be decomposed as the union of four sets (from now on we use the notion $XY$ to denote the intersection of the sets $X$ and $Y$ ):

D = P \tilde{P} + PÑ + N \tilde{P} + NÑ

where

$P \tilde{P}$ : true positive set of the regex classifier relative to human;
$PÑ$ : false negative set of the regex classifier relative to human;
$N \tilde{P}$ : false positive set of the regex classifier relative to human; and
$NÑ$ : true negative set of the regex classifier relative to human.

Notice that, since $P$ and $N$ are unsamplable, none of the above sets ( $P \tilde{P}$ , $PÑ$ , $N \tilde{P}$ , or $NÑ$ ) is samplable.

As described above, the performance of the regex classifier development process depends on its ability to present users with false positives $N \tilde{P}$ and false negatives $PÑ$ . When $\tilde{P} ≪ Ñ$ , the false negative items are less recoverable, in the sense that the probability of sampling a false negative item is much smaller than false positive.

Let us use an example to show this. Suppose the data size is $| D | = 10, 000$ and a regex classifier identified 1000 positive items $| \tilde{P} | = 1000$ with 500 false positive and 500 false negative: $| N \tilde{P} | = 500$ and $| PÑ | = 500$ . Since the false positive items are in the samplable set $\tilde{P}$ , we can sample from $\tilde{P}$ to find false positive items. The probability of sampling a false positive item from $\tilde{P}$ is $500 ∕ 1000 = 0.5$ . On the other hand, false negative items are in the samplable set $Ñ$ , which contains $10000 - 1000 = 9000$ items. The probability of sampling a false negative item from $Ñ$ is $500 ∕ 9000 \approx 0.056$ .

The above example shows that, when developing a regex classifier, it is hard for the machine to find false negatives — that is, to find examples of items that the human would classify as positive but the regex classifier does not. This means that positive cases outside of the scope of the current regular expression list are difficult for the regex classifier to identify, which causes the low recall problem.

Here we ask whether it is possible to use a neural network model trained from the regex coded data to identify false negative items. For example, if a regex list for the code “education" contains “teach", “student" and “school", a neural network model may be able to tell that the items containing “class", “book" should be included in the positives. Thus, if we sample items that the regex classified as negative but neural network model classified as positive, we may be able to increase the probability of finding examples that the human rater would code as positive but the regex classifier would not.

Consider a neural network model that classifies $D = \tilde{\tilde{P}} + \tilde{Ñ}$ . The regex false negative set $PÑ$ is decomposed by the neural network classifier as

PÑ = PÑ \tilde{\tilde{P}} + PÑ \tilde{Ñ} .

We are mostly interested in the items that regex classifies as negative but neural network model classifies as positive. We call the set of such items Negative Reversion Set, which can be written as

Ñ \tilde{\tilde{P}} = PÑ \tilde{\tilde{P}} + NÑ \tilde{\tilde{P}} .

Notice that the negative reversion set $Ñ \tilde{\tilde{P}}$ is the intersection of the regex negative set (items coded negative by the regex) $Ñ$ and the neural network positive set (items coded positive by the neural network) $\tilde{\tilde{P}}$ . Since both $Ñ$ and $\tilde{\tilde{P}}$ are samplable, the negative reversion set $Ñ \tilde{\tilde{P}}$ is samplable.

2.6 Research question

In what follows, we ask two research questions:

2.6.1 RQ1

Is the probability of finding a regex false negative item higher from the negative reversion set $Ñ \tilde{\tilde{P}}$ than from the regex negative set $Ñ$ ? In other words, are the false negatives denser in the negative reversion set $Ñ \tilde{\tilde{P}}$ than in the regex negative set $Ñ$ ?

We define the false negative density $d_{A}$ of a set $A$ as the proportion of the number of false negative items in the set $A$ . That is,

d_{A} = \frac{| PÑA |}{| A |} .

Thus, the false negative density of a negative reversion set $Ñ \tilde{\tilde{P}}$ is

d_{Ñ \tilde{\tilde{P}}} = \frac{| PÑ \tilde{\tilde{P}} |}{| Ñ \tilde{\tilde{P}} |},

and the false negative density of a regex negative set $Ñ$ is

d_{Ñ} = \frac{| PÑ |}{| Ñ |} .

Using the notation of false negative density, the mathematical form of this research question is whether or not the following equation holds:

d_{Ñ \tilde{\tilde{P}}} ≫ d_{Ñ}

(1)

2.6.2 RQ2

If a set $A$ is found dense with false negatives, does it also has an acceptable false negative recovery rate?

Sampling false negatives in a denser set certainly helps. However, it is also important that the denser set should be large enough to include a certain proportion of false negatives. We define the false negative recovery rate $r_{A}$ of a set $A$ as the proportion of false negatives included in the set $A$ , that is

r_{A} = \frac{| PÑA |}{| PÑ |} .

(2)

So, we ask whether or not the false negative recovery rate of the negative reversion set $r_{Ñ \tilde{\tilde{P}}}$ is large enough.

2.6.3 General method

To answer these questions, we investigate a text data set with full regex lists developed and validated for multiple codes. The full regex lists coded data is used as “true human ratings”. We then randomly sample a partial regex list from the full regex list of each code. Partial regex lists are treated as the regex classifiers under development. Neural network models are built from the data coded by these partial regex lists. So, given this data set, we are able to obtain “human ratings" (actually full regex list coding), regex classifier (actually partial regex classifier) and neural network classifier (trained on partial regex classifier). The negative reversion sets are then determined from these three classifications. We are then able to compute the false negative density and the false negative recovery rate of the obtained negative reversion sets to get the answers to our research questions.

3. METHODS

3.1 Data

Table 2: Code definition.
Code	Description
CONSTRAINTS	Referring to inputs: material, processing method, surfactant, and CNT.
PERFORMANCE	Referring to attributes: flus, blood cell reactivity, marketability, cost, or reliability.
COLLABORATION	Facilitating a joint meeting or the production of team design products.
DESIGN	Referring to design and development prioritization, tradeoffs, and design decisions.
DATA	Referring to or justifying decisions based on numerical values, results tables, graphs, research papers, or relative quantities.
REQUESTS	Referring to or justifying decisions based on internal consultant’s requests or patient’s health or comfort.

The data used in this study consists of 50,818 participant utterances collected from novice engineering design teams participating in an engineering virtual internship Nephrotex, in which students worked as interns at a fictitious company that designs and manufactures ultrafiltration membranes for hemodialysis machinery used to treat end-stage renal failure[8]. Table 2 shows the definition of six codes defined by previous researchers, including Tech Constraints, Performance, Collaboration, Design, Data and Requests.

Table 3: Regex lists for each code, the base rates (BR), and the kappas between human rater 1 (H1) and human rater 2 (H2), human rater 1 and computer (C) and human rater 2 and computer.
Code	Regex	BR(%)	H1-H2	H1-C	H2-C
CONSTRAINTS	\bPESPVP, \bdry-jet, \bnegative charge, \bsurfactant, \bchemical, \bvapor deposition polymerization, \bjet \bPMMA, \bPRNLT, \bmanufacturing process, \bmaterials, \bphase inversion, \bvapor, \bsteric, \bPolyamide, \bnano, \bbiological, \bprocesses, \bpolysulfone, \bhydro, \bcarbon nanotube, \bCNT	16.086	0.96	1.00	0.96
PERFORMANCE	\bafforda, \bBCR, \bflux, \bexpensive, \bmarketa, \bcharacteristic, \bcatagories, \bsafe, \bprice, relia, \bblood cell, bility, \bcost	14.508	0.88	0.93	0.84
COLLABORATION	\bmeeting, \bwe all, \bdiscussion, \bwhat should, \beverybody, \bwe could, \bdo we, \bteammates, \bshar, (.?\bpeople.?\bteam.?), (.?\bteam.?\bpeople.?), \bwe should, \bsuggesting, \bshould we	8.861	0.76	0.87	0.76
DESIGN	\bfinal decision, \bdecision, \bwent with, \bbased each design, \bbalance, \bsacrifice, \bsay the first, \bpick, \bI think we should, \bwe had to find, \bbalance, \bmaybe use, \bwe could, \bare we doing, \bcompromise, \bwe changed, \bstick with, \bchoosing, \bdecide, \bliked best, \bbalancing, \bshould we raise, \bimprove the design, \bIm trying that one, \bhow did you design, \bchoose, \bwe want to design, (.?\bincrease.?\bdesign.?), (.?\bdesign.?\bincrease.?), \btargeted, (.?\bcould be.?\bdesign.?), (.?\bdesign.?\bcould be.?), \bI would say, \bwe raised, \bdecrease, \bcomparing, \bsuperior, (.?\bwe could.?\bdesign.?), (.?\bdesign.?\bwe could.?), (.?\bbest.?\boption.?), (.?\boption.?\bbest.?), \bchose \beither way, \blet’s go with, \bwe do it like, \bchoice, (.?\bI think.?\bbest.?), (.?\bbest.?\bI think.?), \bwe can do, (.?\bI think.?\bsubmit.?), (.?\bsubmit.?\bI think.?), \bdo we want, \btradeoff, \bbest way, \bmanipulated, \bminimize, \btrade off \bchose	10.291	0.89	0.86	0.84
DATA	(.?\blowest.?\bcheapest.?), (.?\bcheapest.?\blowest.?), \bperformed well, \bmaximizes, \bhad great reliability, \bresult, \brates, \bscore, \b(?	10.405	0.94	0.9	0.89
REQUESTS	\buser, \bDuChamp, \bPadma, \bsafety, \bhospital, \bstandard, \bcomfort, \brecommendations, \bRudy, (^?:(?!\bexternal).)\bconsultant(?!.\bexternal), \bMichelle, \bminimum, \bWayne, \brequest, \bsatisfy, \bpatient, \bProctor, \binternal consultant, \bHernandez, \brequirement \bAnderson, \bunacceptables, \bclient, \bAlan, \bRao	7.059	0.88	0.94	0.94

Using nCoder tool (https://app.n-coder.org/), researchers developed and validated the regex lists. Table 3 shows the regex list for each code, together with “base rate” (BR) and kappa values. The base rate of a code was the proportion of items in the data set the code occurred. The kappa values were computed on the ratings from two human raters (H-1, H-2) and the regex classifier (C). Because of the high kappa values, we considered these regex lists as “complete" and represent the “true classification" by human raters. In the discussions below, we use “full regex classification" to replace “human classification".

We decomposed the items in the regex lists if they were connected by a pipe symbol “|". For example, if an item was “r1|r2", then it was decomposed as two items “r1" and “r2". Of course, all items in the list for a given code could be composed back as a single regex by re-connecting them with a pipe symbol “|". We decomposed the regex in this way so that we could more meaningfully sample partial regex lists.

3.2 Data splitting

The data set $D$ was randomly split into a training set $S$ and a test set $T$ , each of which consisted of 25,409 items. The training set $S$ was used for sampling items to train neural network models, while test set $T$ was used for computing final results.

3.3 Coding by three classifiers

3.3.1 Full regex coding

Full regex lists for the six codes were used to code the whole data set $D$ , which formed the “true classification" of the whole data $D = P_{D} + N_{D}$ . Consequently, the training set $S$ and the test set $T$ are also “truly" classified as $S = P_{S} + N_{S}$ and $T = P_{T} + N_{T}$ . Under this classification, the positive rates (base rates) for the six codes range from 7% to 16% (see Table 3).

3.3.2 Partial regex coding

For a given code, a partial regex list was constructed using the following procedure:

Start with an empty regex list $L = {\emptyset}$ and full regex list $R_{c}$ for a code $c$ ;
Randomly select a regex $r \in R_{c}$ and add it to the partial regex list $L$ ;
Code the whole data set $D$ by the partial list $L$ to produce ${\tilde{P}}_{D ∕ L}$ ;
Compute the number of positive items $| {\tilde{P}}_{D ∕ L} |$ coded by $L$ ;
If $| {\tilde{P}}_{D ∕ L} | > \frac{| P_{D} |}{2}$ , end the procedure; otherwise go back to step 2.

Through this procedure, the number of positive items classified by a partial regex list $L$ is equal to or greater than half of the true positive items. Each partial list $L$ decomposed the training set and test set into the following samplable sets (for parsimony, we define ${\tilde{P}}_{A} \equiv {\tilde{P}}_{A ∕ L}$ ):

${\tilde{P}}_{S}$ : regex positives in training set;
$\tilde{P_{T}}$ : regex positives in test set;
$\tilde{N_{S}}$ : regex negatives in training set; and
$\tilde{N_{T}}$ : regex negatives in test set.

3.3.3 Neural network coding

In this paper, the neural network models were trained based on the classification of partial regex classifiers. For a given partial regex classifier and a given sample size $n$ , a random sample $s_{n} \in S$ with size $n$ was taken from the training set. Each item in the sample contained two fields: the text field $X$ and the classification value $Y$ (1 when the regex list was matched and 0 otherwise). The text field $X$ is used as the input and the partial regex classification value $Y$ is used as the output to train a predictive LSTM neural network model. The testing set was then coded by the predict function of the LSTM model, with the cutoff probability 0.5. Thus, the neural network model classified the test set into the samplable sets:

$\tilde{\tilde{P_{T}}}$ : neural network positive in test set; and
$\tilde{\tilde{N_{T}}}$ : neural network negative in test set.

3.3.4 Sample size and repetition of partial regex lists

In training the neural network models, we used five different sample sizes: $n = 100, 200, 400, 800, 1600$ . In order to reduce the random effect in partial regex construction, 12 random partial regex lists were drawn for each code using the partial regex construction procedure. So, for each of the six codes, the test set had the following classifications:

1 “true classification" $T = P + N$ ;
12 partial regex list classification $T = \tilde{P_{i}} + \tilde{N_{i}}$ , $(i = 1, 2, \dots, 12)$ ;
60 neural network classification (12 partial regex list, 5 sample sizes each) $T = \tilde{\tilde{P_{in}}} + \tilde{\tilde{N_{in}}}$ , $(i = 1, 2, \dots, 12; n = 100, 200, 400, 800, 1600)$ .

In the notions above, $\tilde{P_{i}}$ and $\tilde{N_{i}}$ were the positive and negative set, respectively, classified by the $i^{th}$ partial regex for the given code; and $\tilde{\tilde{P_{in}}}$ and $\tilde{\tilde{N_{in}}}$ were the positive and negative set, respectively, classified by the neural network model trained on the $i^{th}$ partial regex list with sample size $n$ .

3.4 Performance metrics

Before moving on, we define three measures for the performance of classifiers: precision, recall and Cohen’s $κ$ . For a given classifier, denote the proportion of true positives, false positives, false negatives and true negatives by $tp$ , $fp$ , $fn$ and $tn$ , respectively.

The precision of a classifier is the ratio of true positive to the sum of true positive and false positive, namely
$precision = \frac{tp}{tp + fp} .$
The recall of a classifier is the ratio of true positive to the sum of true positive and false negative, namely
$recall = \frac{tp}{tp + fn} .$
The Cohen’s kappa $κ$ of a classifier is the ratio of the difference between observed probability and chance probability to one minors chance probability, namely,
$κ = \frac{p_{o} - p_{c}}{1 - p_{c}} .$
where
$p_{o} = tp * fp,$
and
$p_{c} = fp * fn + (1 - fp) * (1 - fn) .$

4. RESULTS

4.1 Single model comparison

Table 4 shows an example classification on code “Tech Constraints" with its full regex list, one randomly constructed partial regex list and one neural network model trained from the partial regex list with sample size 400.

In this example, the classification of the test set by the full regex classifier, which was considered the “true classification", yielded 3976 positive items (set $P$ ) and 21,431 negative items (set $N$ ). Notice that there were far more negative items than positive items. The partial regex classifier correctly identified 2,133 positive items (set $P \tilde{P}$ ). However, it falsely classified 1845 positive items as negative (set $PÑ$ ). Since the partial regex was a subset of the full regex list, any item matched by the partial regex was in turn matched by the full regex. In other words, any item not matched by the full regex was not matched by the partial regex. Thus, no negative item was falsely classified as positive (set $N \tilde{P}$ ); and the partial regex classifier agreed with the full regex classifier on all 21,431 negative items (set $NÑ$ ). As a result, the partial regex got a larger negative set $Ñ = PÑ + NÑ$ with a total of 23,276 items. The false negative density in the negative set $Ñ$ was thus $d_{Ñ} = 1845 ∕ 23276 \approx 7.92 %$ .

The third column of the table shows the classification results of the neural network model trained on the data classified by the given partial regex list with sample size 400. There were 1170 items that were correctly classified by both partial regex list and the trained neural network model (set $P \tilde{P} \tilde{\tilde{P}}$ ). 963 positive items were correctly classified by the partial regex list but falsely classified as negative by the neural network model (set $P \tilde{P} \tilde{Ñ}$ ). Most interestingly, there were 288 positive items that were falsely classified as negative by the partial regex list but correctly reversed as positive by the neural network model (set $PÑ \tilde{\tilde{P}}$ ). 1557 positive items were falsely classified as negative by both the partial regex list and neural network model. For the 21,431 negative items, the neural network falsely classified 302 items as positive (set $NÑ \tilde{\tilde{P}}$ ) and correctly classified 21,129 items as negative (set $NÑ \tilde{Ñ}$ ).

The negative reversion set $Ñ \tilde{\tilde{P}}$ was the union of the sets $PÑ \tilde{\tilde{P}}$ and $NÑ \tilde{\tilde{P}}$ , which contained 288 correctly reversed items and 302 falsely reversed items. Therefore, the false negative density in the negative reversion set $Ñ \tilde{\tilde{P}}$ was $d_{Ñ \tilde{\tilde{P}}} = 288 ∕ (288 + 302) \approx 48.81 %$ , which was much larger than the density in the regex negative set $d_{Ñ} = 7.92 %$ .

This example gives us a positive answer to our first research question. That is, the false negative density in the negative reversion set is much higher than in the regex negative set.

To answer the second question, we computed the false negative recovery rate in the negative reversion set. From Equation 2, we had $r_{Ñ \tilde{\tilde{P}}} = 288 ∕ 1845 \approx 16 %$ .

If our goal is to find all false negatives, this number is not very high, because $84 %$ false negatives are still sparsely distributed in the regex negative set $Ñ$ . However, we argue that this number is large enough for constructing iterative methods, which we will talk more about in the discussion section.

Table 4: An example of false negative recovery for Tech Constraints with training size 400.
Full Regex	Partial Regex	Neural Network
$P$ (3976)	$P \tilde{P}$ (2133) $PÑ$ (1845)	$P \tilde{P} \tilde{\tilde{P}}$ (1170) $P \tilde{P} \tilde{Ñ}$ (963) $PÑ \tilde{\tilde{P}}$ (288) $PÑ \tilde{Ñ}$ (1557)
$N$ (21,431)	$N \tilde{P}$ (0) $NÑ$ (21,431)	$N \tilde{P} \tilde{\tilde{P}}$ (0) $N \tilde{P} \tilde{Ñ}$ (0) $NÑ \tilde{\tilde{P}}$ (302) $NÑ \tilde{Ñ}$ (21,129)

Missing item recovery — Figure 3: False negatives density in partial regex negatives versus in negative reversion set.

4.2 Average false negative density

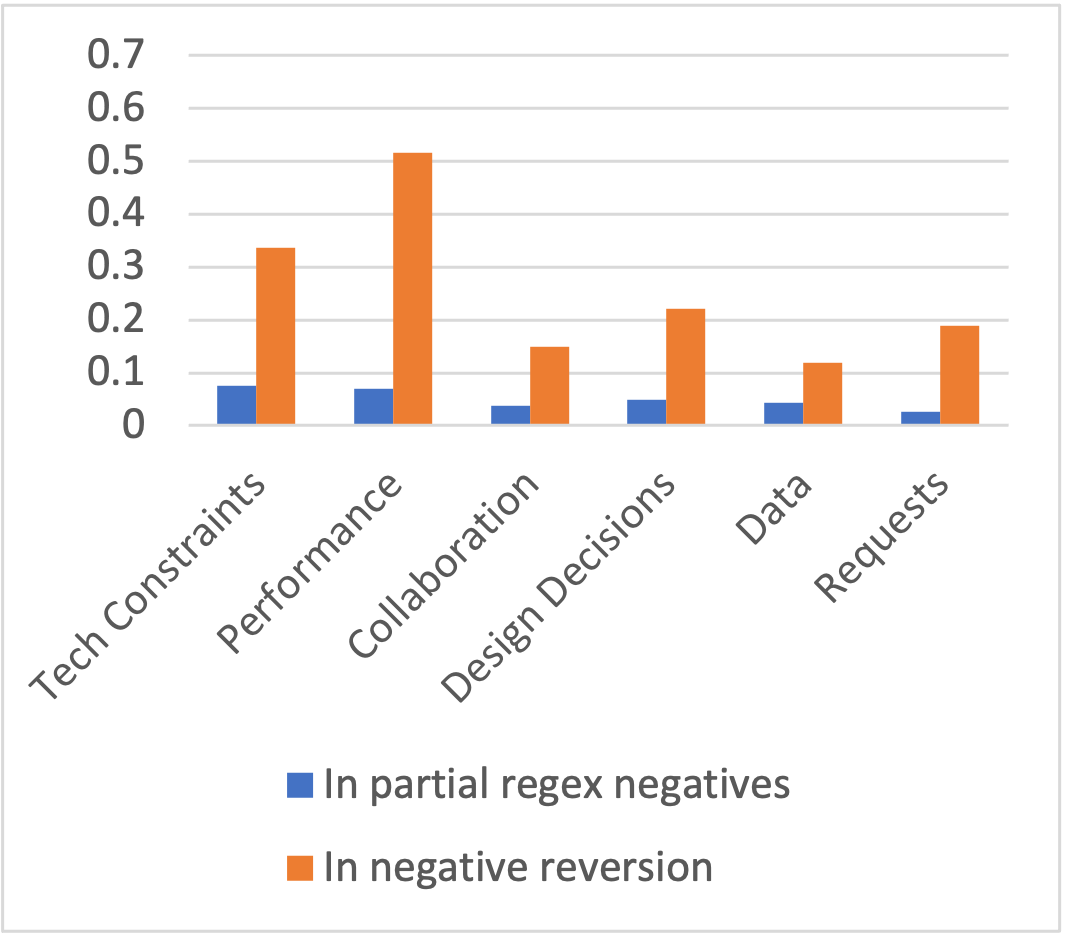
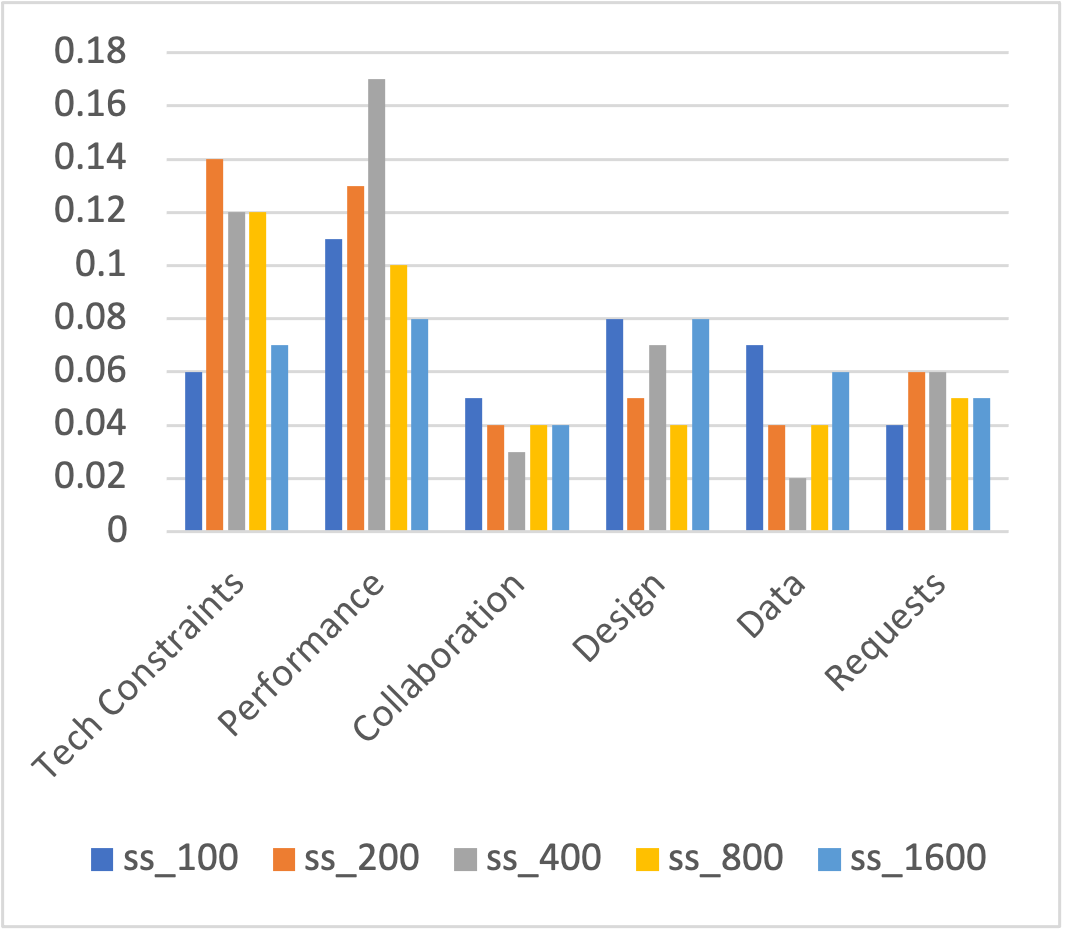
The above example showed false negative density and the false negative recovery rate in the negative conversion set for one code, one random partial regex list and one neural network model with sample size 400. To answer our research questions more reliably, we computed the average false negative density for each code with 12 randomly drawn partial regex lists. The results show that the false negative density for all codes were several times higher in the negative reversion set $Ñ \tilde{\tilde{P}}$ than in the regex negative set $Ñ$ . Figure 3 shows the results for sample size=400. While the density $d_{Ñ}$ in the regex negative set ranged from 3% to 8%, the density $d_{Ñ \tilde{\tilde{P}}}$ in the negative reversion set ranged from 12% to 52%. For example, the density for the code “Performance" increased from $d_{Ñ} = 7 %$ to $d_{Ñ \tilde{\tilde{P}}} = 52 %$ .

4.3 Average false negative recovery rate

For each code, we computed the average false negative recovery rate over 12 randomly drawn partial regex lists. Table 5 shows, with neural network training size=400, the number of items in sets $PÑ \tilde{\tilde{P}}$ and $PÑ \tilde{Ñ}$ and false recovery rate as percentages. The average false negative recovery rates ranged from 1.88% to 16.88% and the average number of false negative items included in the negative reversion set ranged from 19.67 to 270.17.

Table 5: False negative recovery rate, training size=400
Code	$PÑ \tilde{\tilde{P}}$	$PÑ \tilde{Ñ}$	$r$ (%)
Tech Constrains	195.83	1579.67	11.03
Performance	270.17	1338.00	16.80
Collaboration	23.75	900.58	2.57
Design	76.67	1908.17	6.53
Data	19.67	1027.67	1.88
Requests	38.25	615.25	5.85

Density all sizes — Figure 4: False negative density in negative reversion set for all sample sizes.

4.4 Sample size effect

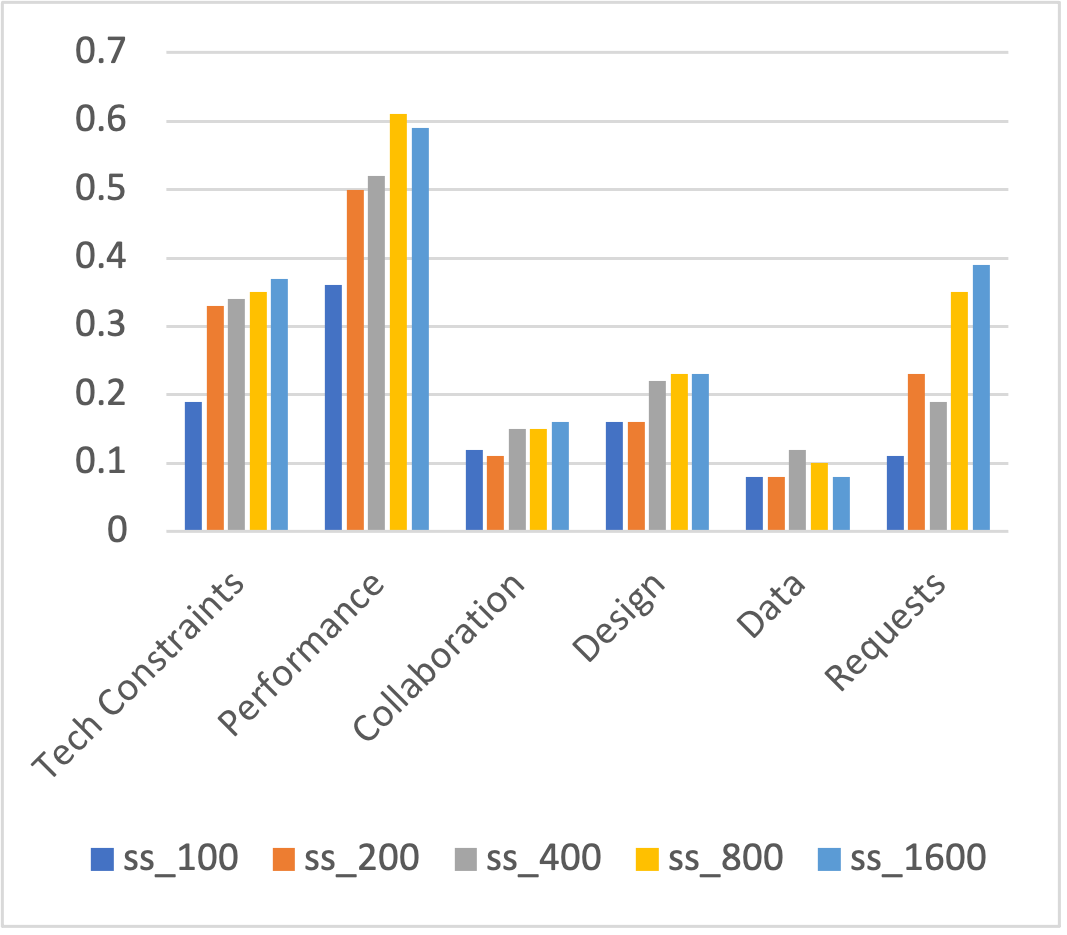
In the above, we only showed the results for the neural network models trained from sample size $n = 400$ . Figure 4 and Figure 5 show the average false negative density and false negative recovery rate in the negative reversion set for each code as a function of neural network training size. For the codes “Tech Constraints", “Collaboration" and “Design", the density change was very small after size 400. For code “Performance" and “Requests", the density for larger training size was larger. However, they suffered from reduced false negative recovery rate.

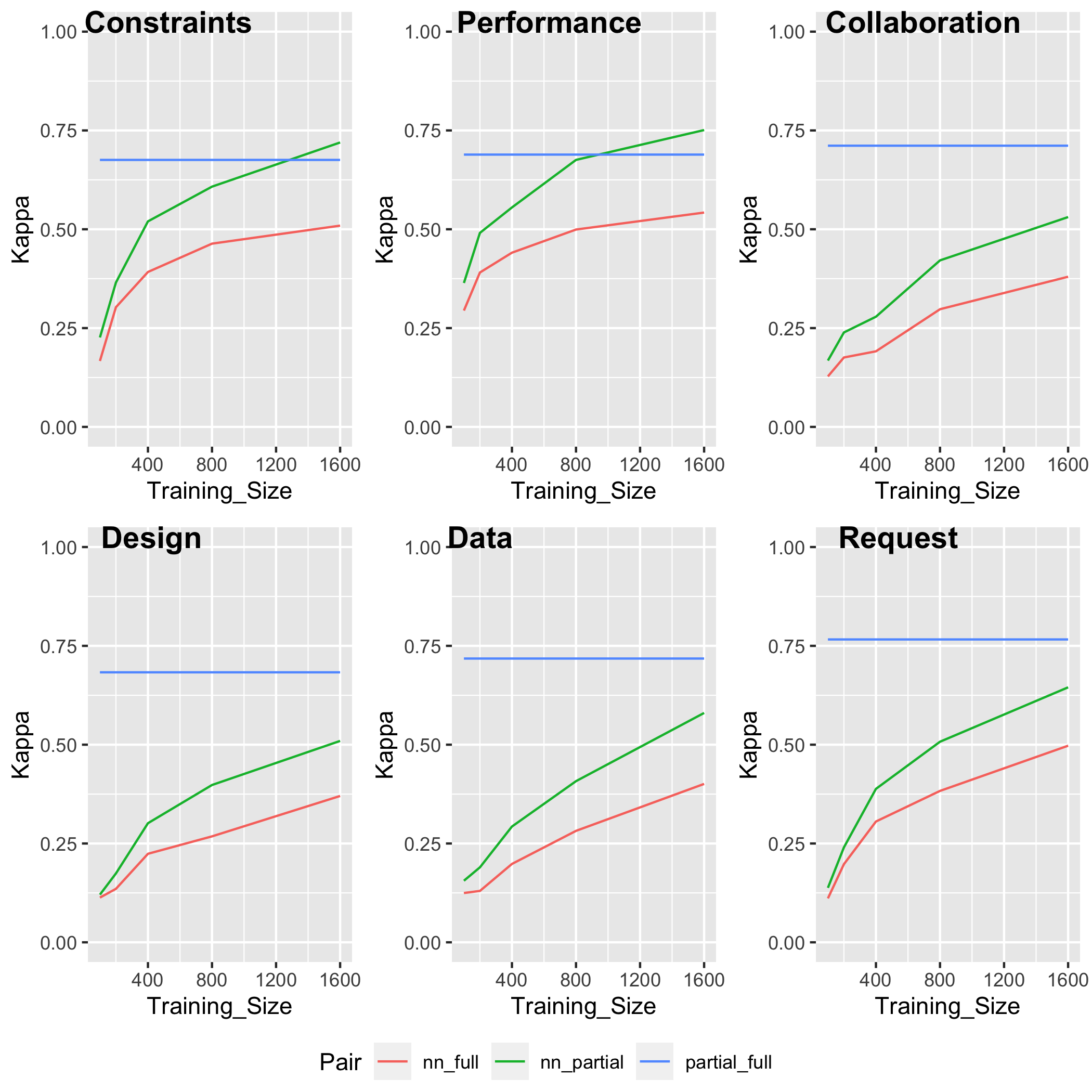
Kappas: Full regex, partial regex and neural network models — Figure 6: Kappa as functions of training size between three pairs of coding: partial regex and full regex coding, neural network and full regex coding, and and neural network and partial regex coding.

We also computed Cohen’s kappa between different models. Figure 6 shows the mean Cohen’s kappas for each code as functions of sampling size for neural network model. The kappa means were computed over the 12 partial regex lists for each code. The blue lines are the kappas between full regex and partial regex lists. They are horizontal lines because they have nothing to do with the sample size. The green lines are kappas between partial regex lists and neural network models. As sample size increases, the green lines increases. That indicates that neural network models could be close to the partial regex list model as the sample size increases. For codes “Tech Constraints" and “Performance", the green lines even go beyond the blue lines when the sample size is large. This is normal because the neural network models were trained from partial regex list. The red lines are kappas between the full regex and neural network models. Although the red lines also increase, they never go beyond the blue lines. That indicates that, although neural network models may help identify items missed in partial regex list, they don’t perform better than the regex classifier from which they are trained.

5. CONCLUSIONS

In this study, we used neural network models trained from partial regex classifier to help identify the false negatives from partial regex classifiers. The so called negative reversion set $Ñ \tilde{\tilde{P}}$ was of our most interest in this study. This set consisted of conflict items that the partial regex classifier coded as negative but the neural network classifier coded as positive. Since the neural network classifiers was trained from the data coded by the partial regex classifiers, the negative reversion sets were actually error sets - the false positive sets relative to the partial regex coded data. That is, the neural network models didn’t correctly predict how the partial regex classifiers code such items. However, our study showed that this “error set" had a much higher density of regex false negatives. This indicates that the neural network models had some ability in detecting the error contained in the training data. It is unclear how this happened. Our current theory is that, since the neural network model was built on semantic representations (word embedding layer captures the word meaning and the LSTM layer captures the word order information), it could be able to detect certain violations of semantic consistency. For example, if “table" and “chair" are included in a partial regex list, the neural network model may suggest that “furniture" shouldn’t be excluded.

The results show the differences of the density increases among codes. The increased density in the false negative reversion set doesn’t correlate to the original density in the regex false negative set. The source of the difference is unknown. However, the fact that the density in the false negative reversion set is from 3 to 12 times higher suggests that this technique could improve classifier performance.

The results showed that false negative recovery rate ranged from 2% to 17%, depending on the specific code and neural network training size. This indicates that, while it is easier to find false negative items from the negative reversion set, many false negative items remain in other sets. We suggest that, when searching for false negative items, the negative reversion set and the whole regex negative set should both be considered.

The training size issue in this study is more complex. In general, more training data results in better neural network models. However, in our case, we are expecting a larger “error set" $Ñ \tilde{\tilde{P}}$ . When the training size is too large, the “error set" shrinks and thus reduces the false negative recovery rate. From our study, it appears that a training size of approximately 400 is adequate.

More generally, our study is limited by the use of one specific data set, six specific codes, and a specific ratio (1:2) between the partial regex and the full regex. In practice, the partial regex corresponds to the regex list under development and the full regex corresponds to the human understanding of the code. When the partial regex is close to the “full regex", the density in the negative reversion set may become small.

While, of course, training the neural network models from manually coded data would produce a better predictor, it would require a human rater to code a large number of items. But, as we argued above, even if enough manual coding could be provided, training a neural network model directly from the manually coded data will result in a classifier that is hard to interpret and defend. Instead, we suggest using an imperfect neural network model to augment regex-based classification, so that when a regex classifier codes a positive item, it will be clear to researchers and end users why each item has been coded.

The last but not least, we didn’t use real human coding in this study, which limited our investigation on false negative items only, because a partial regex classifier will never have false positive prediction in relation to a full regex classifier. However, in the case of real human coding, false positives are likely to occur. Similar to the negative reversion set, we may define a positive reversion set as the set of items for which the regex classifier coded as positive but the human rater coded as negative. It could be the case that the positive reversion set also contains denser false positives. However, this is less important when the positive rate is small.

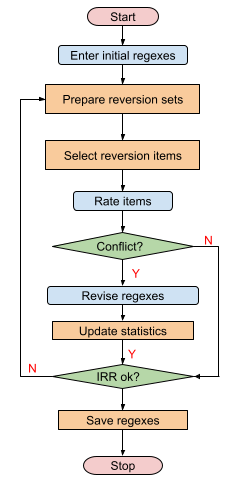
Figure 7: Neural network assisted regex development.

To conclude this paper, we propose the following iterative procedure for better development of regex classifiers (see Figure 7):

The user enters initial regex list for development;
A machine learning model is trained based on the initial regex list classification and prepares reversion sets;
The computer selects highly likely conflict items suggested by machine learning model;
The user rates the item ;
If a conflict occurs, the user resolves the conflict and updates the regex list;
The computer computes agreement statistics (IRR) based on the ratings from the user, regex list and neural network model;
If the statistics show that the IRR is not high enough, go back to the reversion set preparation step and reiterate the process;
If the statistics show high agreement, end the process.

6. ACKNOWLEDGMENTS

This work was funded in part by the National Science Foundation (DRL-1713110, DRL-2100320,LDI-1934745), the Wisconsin Alumni Research Foundation, and the Office of the Vice Chancellor for Research and Graduate Education at the University of Wisconsin-Madison. The opinions, findings, and conclusions do not reflect the views of the funding agencies, cooperating institutions, or other individuals.

7. REFERENCES

X. Bai. Text classification based on lstm and attention. In Thirteenth International Conference on Digital Information Management (ICDIM), pages 29–32, 2018.
R. Baker. Data mining for education. International encyclopedia of education, 7(3):112–118, 2010.
D. M. Blei and A. Y. Ng. Latent dirichlet allocation. Journal of Machine Learning Research, 3(4-5):993–1022, 2003.
Z. Cai, B. Eagan, N. M. Dowell, J. W. Pennebaker, D. W. Shaffer, and G. A. C. Epistemic network analysis and topic modeling for chat data from collaborative learning environment. In Proceedings of the 10th International Conference on Educational Data Mining, pages 104–111, 2017.
Z. Cai, A. Siebert-Evenstone, B. Eagan, and D. W. Shaffer. Using topic modeling for code discovery in large scale text data. In Advances in Quantitative Ethnography: ICQE Conference Proceedings, pages 18–31, February 2021.
K. Charmaz. Constructing grounded theory. Sage, London, 2006.
N.-C. Chen, M. Drouhard, R. Kocielnik, J. Suh, and C. R. Aragon. Using machine learning to support qualitative coding in social science: Shifting the focus to ambiguity. ACM Trans. Interact. Intell. Syst., 8(2):9:1–9:20, jun 2018.
N. Chesler, A. Ruis, W. Collier, Z. Swiecki, G. Arastoopour, and D. Shaffer. A novel paradigm for engineering education: virtual internships with individualized mentoring and assessment of engineering thinking. Journal of Biomechanical Engineering, 137(2):1–8, 2015.
K. Crowston, X. Liu, E. Allen, and R. Heckman. Machine learning and rule-based automated coding of qualitative data. In Proceedings of ASIST 2010, pages 1–2, October 2010.
D. Gautam, Z. Swiecki, D. W. Shaffer, A. C. Graesser, and V. Rus. Modeling classifiers for virtual internships without participant data. In Proceedings of the 10th International Conference on Educational Data Mining, pages 278–283, 2017.
B. Glaser and A. Strauss. The discovery of grounded theory: Stretegies for qualitative research. Aldine, Chicago, 1967.
A. C. Graeser, X. Hu, V. Rus, and Z. Cai. Conversation-based learning and assessment environments. In D. Yan, A. A. Rupp, and P. W. Foltz, editors, Handbook of Automated Scoring, pages 383–402, New York, February 2020. Chapman and Hall/CRC.
G. Li and G. Jiabao. Liu, gang, and jiabao guo. "bidirectional lstm with attention mechanism and convolutional layer for text classification. Neurocomputing, 337:325–338, 2019.
Y. Li, R. Krishnamurthy, S. Raghavan, and S. Vaithyanathan. Regular expression learning for information extraction. In Proceedings of the 2008 Conference on Empirical Methods in Natural Language Processing, pages 21–30, October 2008.
D. Shaffer. Quantitative Ethnography. Cathcart Press, Madison, WI, 2017.
D. W. Shaffer and A. R. Ruis. How we code. In Advances in Quantitative Ethnography: ICQE Conference Proceedings, pages 62–77, February 2021.

[1] X. Bai. Text classification based on lstm and attention. In Thirteenth International Conference on Digital Information Management (ICDIM), pages 29–32, 2018.

[2] R. Baker. Data mining for education. International encyclopedia of education, 7(3):112–118, 2010.

[3] D. M. Blei and A. Y. Ng. Latent dirichlet allocation. Journal of Machine Learning Research, 3(4-5):993–1022, 2003.

[4] Z. Cai, B. Eagan, N. M. Dowell, J. W. Pennebaker, D. W. Shaffer, and G. A. C. Epistemic network analysis and topic modeling for chat data from collaborative learning environment. In Proceedings of the 10th International Conference on Educational Data Mining, pages 104–111, 2017.

[5] Z. Cai, A. Siebert-Evenstone, B. Eagan, and D. W. Shaffer. Using topic modeling for code discovery in large scale text data. In Advances in Quantitative Ethnography: ICQE Conference Proceedings, pages 18–31, February 2021.

[6] K. Charmaz. Constructing grounded theory. Sage, London, 2006.

[7] N.-C. Chen, M. Drouhard, R. Kocielnik, J. Suh, and C. R. Aragon. Using machine learning to support qualitative coding in social science: Shifting the focus to ambiguity. ACM Trans. Interact. Intell. Syst., 8(2):9:1–9:20, jun 2018.

[8] N. Chesler, A. Ruis, W. Collier, Z. Swiecki, G. Arastoopour, and D. Shaffer. A novel paradigm for engineering education: virtual internships with individualized mentoring and assessment of engineering thinking. Journal of Biomechanical Engineering, 137(2):1–8, 2015.

[9] K. Crowston, X. Liu, E. Allen, and R. Heckman. Machine learning and rule-based automated coding of qualitative data. In Proceedings of ASIST 2010, pages 1–2, October 2010.

[10] D. Gautam, Z. Swiecki, D. W. Shaffer, A. C. Graesser, and V. Rus. Modeling classifiers for virtual internships without participant data. In Proceedings of the 10th International Conference on Educational Data Mining, pages 278–283, 2017.

[11] B. Glaser and A. Strauss. The discovery of grounded theory: Stretegies for qualitative research. Aldine, Chicago, 1967.

[12] A. C. Graeser, X. Hu, V. Rus, and Z. Cai. Conversation-based learning and assessment environments. In D. Yan, A. A. Rupp, and P. W. Foltz, editors, Handbook of Automated Scoring, pages 383–402, New York, February 2020. Chapman and Hall/CRC.

[13] G. Li and G. Jiabao. Liu, gang, and jiabao guo. "bidirectional lstm with attention mechanism and convolutional layer for text classification. Neurocomputing, 337:325–338, 2019.

[14] Y. Li, R. Krishnamurthy, S. Raghavan, and S. Vaithyanathan. Regular expression learning for information extraction. In Proceedings of the 2008 Conference on Empirical Methods in Natural Language Processing, pages 21–30, October 2008.

[15] D. Shaffer. Quantitative Ethnography. Cathcart Press, Madison, WI, 2017.

[16] D. W. Shaffer and A. R. Ruis. How we code. In Advances in Quantitative Ethnography: ICQE Conference Proceedings, pages 62–77, February 2021.