ABSTRACT

Stealth assessment in game-based learning environments has demonstrated significant promise for predicting student competencies and learning outcomes through unobtrusive data capture of student gameplay interactions. However, as machine learning techniques for student competency modeling have increased in complexity, the need for substantial data to induce such models has likewise increased. This raises scalability concerns, as capturing game interaction data is often logistically challenging yet necessary for supervised learning of student competency models. The generalizability of such models also poses significant challenges, and the performance of these models when applied to new domains or gameplay scenarios often suffers. To address these issues, we introduce a zero-shot learning approach that utilizes conditional generative modeling to generalize stealth assessment models for new domains in which prior data and competency labels may not exist. We evaluate our approach using observed student interactions with a game-based learning environment for introductory genetics. We use a conditional generative model to map latent embeddings of genetics concepts and student competencies to student gameplay patterns, enabling the generation of synthetic gameplay data associated with concepts and game levels that have not been previously introduced. Results indicate the zero-shot learning approach enhances the performance of the competency models on unseen game levels and concepts, pointing to more generalizable stealth assessment models and improved prediction of student competencies.

Keywords

INTRODUCTION

Game-based learning has been shown to be effective at promoting student engagement and fostering enhanced learning experiences [7, 31]. These environments can complement traditional learning methods and help students acquire “21st century skills” such as digital literacy, creative thinking, and knowledge acquisition [4]. Further, game-based learning environments can enable educators to unobtrusively analyze student behavior through stealth assessment for the purpose of improving learning outcomes [9, 35]. Stealth assessment, offers a systematic approach for constructing data-driven models of student performance derived from evidentiary arguments [6, 29]. Despite these promising benefits, data-driven student modeling techniques are growing in complexity and often require large amounts of training data, which poses significant challenges.

Collecting sufficient data for training student models is often time and resource intensive, raising scalability concerns for stealth assessment frameworks [45]. Practitioners may also find that modeling student behavior in new domains, educational contexts, and populations is infeasible due to data sparsity issues. Further, circumstances may arise where there is no prior data to train stealth assessment models. Examples include where post-test surveys are impractical to administer, such as informal learning environments like museum exhibits, or if a learning concept or in-game problem-solving task is being deployed for the first time. These problems pose significant practical challenges for stealth assessment models.

Few-shot learning has been introduced as an effective method for classification tasks where labeled data may be scarce for certain classes or tasks [11, 23, 26, 45]. In particular, zero-shot learning (ZSL) refers to scenarios where no samples of a specific class are present at training. ZSL forms a mapping between the data and class labels present at training (“seen” data) and data absent from the training set (“unseen” data) using other attributes (semantic data) to bridge the gap between these two domains. ZSL can also address the aforementioned issues with stealth assessment by generating competent augmented data representative of the “unseen” classes, maintaining intra-class variance while promoting inter-class discrimination based on semantic relationships within the data [11, 45]. This allows for effective data augmentation that can be used to train downstream classifiers to make accurate inferences on data samples from new or unseen classes. Because these techniques are designed to work in the absence of training data for new or unseen classes, they can be used to bootstrap new models and help mitigate the “cold start” problem where models make poor inferences due to this lack of class-specific training data [46].

In this work, we propose a generative zero-shot learning approach to improve stealth assessment models for predicting student competencies for certain gameplay levels and educational concepts missing prior student interaction data. We utilize conditional generative adversarial networks and embedding representations of introductory genetics concepts to learn latent mappings between student competencies and gameplay behaviors. By generating synthetic gameplay data conditioned on genetics concept descriptors, the generalizability of the competency models can be enhanced, leading to improved predictive performance. Our approach is evaluated using Geniventure, a game-based learning environment for teaching introductory genetics concepts to middle and high school students. Stealth assessment models induced with augmented student gameplay data are used to assess our generative ZSL approach. There are few zero-shot learning methods applied within educational domains [11, 22, 45]. However, to our knowledge there has not been prior work on addressing the unseen class problem in stealth assessment. We demonstrate that our approach is an effective method for addressing challenges with data sparsity and unseen class labels for student competency models in a game-based learning environment. Finally, we further show that our approach leads to improvement in the predictive performance of student competency models when compared against non-augmented baselines and alternative generative modeling techniques.

RELATed work

This work lies at the intersection of zero-shot learning and stealth assessment, particularly addressing approaches to student competency prediction for a range of genetics concepts, which is a subset of student modeling. We provide an overview of recent work pertaining to student modeling in game-based learning, with a focus on stealth assessment. Additionally, we provide a review of recent zero-shot learning research pertaining to student modeling, in addition to zero-shot learning using generative modeling approaches.

Student Modeling in
Game-Based Learning

Student modeling has been shown to be effective at predicting complex learning processes such as engagement, flow, and the incubation effect [21, 32, 40]. More specifically, student modeling within game-based learning has been shown to positively impact deep learning and higher order thinking [19], promote self-regulated learning during gameplay [20, 34, 42], and address cognitive, affective, and social factors for fostering enhanced learning outcomes [3, 16]. Additionally, student modeling within game-based learning environments has been used to analyze and predict student competency levels in a variety of domains, including physics [41], literacy [40], and computational thinking. Student modeling in educational games has also been used to enable personalized and adaptive learning environments [5]. Spaulding et al. investigate the efficacy of transfer of learned cognitive models between two game-based learning environments [40]. The authors investigate the issue of negative transfer by utilizing Gaussian processes and an instance-weighting approach that considers the similarity between source and target tasks. Additionally, they address the aforementioned “cold-start” problem with a multi-task learning approach. Other studies have explored data-driven approaches for inferring student competencies by modeling their in-game progression through activity log data [12]. Similar data-driven approaches have attempted to design student learning profilers that can inform practitioners in their design of adaptive gamified learning environments tailored to students’ interests and needs. One example is SPOnto, a student profile ontology, that employs a multi-phase pipeline for student classification [29]. By predicting self-reported student type, intelligence type, and learning difficulties, the authors’ approach shows promise for personalized learning systems enabled by student behavioral patterns.

Stealth Assessment

There has been increased emphasis on developing effective and robust stealth assessment frameworks in recent years. By varying multiple input features (e.g., ECD model, sample size, data normality significance levels), Georgiadis et al. find that Gaussian Naïve Bayes and C4.5 models were effective for use in stealth assessment and were capable of handling different data distributions with extreme non-normality [14]. However, these models’ accuracy degrades as ECD models increase in complexity. Shute and Rahimi utilize stealth assessment to establish a link between creativity and the properties of well-established learning games that foster creative behavior and propose a creativity criterion [36]. Using Physics Playground and Bayesian networks, they show that their stealth assessment framework offers a valid measure for inferring creativity and was significantly correlated with other performance-based measures of creativity. In contrast to traditional approaches, deep learning-based methods such as long-short term memory networks (LSTMs) have been utilized as a method to model long-term temporal dependencies within student gameplay behaviors [18]. Min et al. employ LSTMs and n-gram based feed forward neural networks and compare their performance to competitive baselines [24]. By combining students’ pre-learning measures and interaction log data from a game-based learning environment, the LSTM-based approach outperformed both baseline methods and the highest performing FFNN using early prediction metrics. Akram et al. achieve similar results supporting the effectiveness of LSTMs as a student modeling technique [1].

Zero-Shot Learning

Zero-shot learning, first introduced as “zero-data learning” [23], considers the task of recognizing new classes whose instances may not have been seen during training. Recent advances in ZSL have largely been applied in the image and video classification domains, but relatively little work has explored its effectiveness in learning analytics. Wu et al. introduce the “ZSL feedback challenge” utilizing a dataset of 8 assignments with 800 unique solutions to propose a method for attributing feedback to specific sections of student code and to trace knowledge over time [45]. The authors achieve optimal performance by combining a rubric sampling technique with a multimodal variational autoencoder. Their framework can effectively track student growth over time and can provide feedback on non-compiled programs. In an alternative approach, Efremov et al. apply neural program synthesis, a reinforcement learning approach, to generate feedback and step-by-step hints for students from a partial solution [11]. They incorporate abstract syntax tree representations of student code with a tree-based bi-directional LSTM architecture to encode students’ inputs. The learned policy network outperforms state-of-the-art methods such as a continuous hint factory (CHF) and can provide feedback on specific lines of code.

Generative models are another method for approaching the ZSL problem. Mishra et al. introduce a conditional variational autoencoder conditioned on a class embedding vector to reduce domain shift across unseen classes [26]. The generative model is used to produce synthetic training data that is utilized by a downstream classifier. Their generalized zero-shot learning approach is applied to five popular image recognition datasets and is able to achieve state-of-the-art performance using top-k and per class accuracy.

We contribute to this line of research by introducing a zero-shot learning approach to improve the generalizability of stealth assessment models. This work employs conditional generative adversarial networks for creating synthetic gameplay data from concepts for which there was no previous student interaction data available at training. We demonstrate that this method can improve predictive performance of student mastery within unseen game levels and educational concepts, highlighting its potential as a method for generalizing student competency models.

Student Gameplay DATA

Our generative ZSL method is implemented using a dataset captured from students’ interactions with a game-based learning environment designed to teach genetics. By generating features from the students’ gameplay trace data, we are able to induce student competency models without utilizing inherently intrusive or distracting methods such as external assessments or data capture through physical sensors. Student competencies for the different genetics concepts presented in Geniventure are quantified using a post-test knowledge assessment, with different questions corresponding to different concepts within the game’s individual levels. These levels are divided into “seen” and “unseen” groups for evaluation of the ZSL data augmentation performance.

Geniventure Learning Environment

To evaluate the impact of our generative ZSL approach to student competency modeling, we use gameplay interaction log data captured from students engaging with Geniventure. Geniventure is targeted towards middle and high school students (ages 11-18 years) and the overall design of the game is guided by fundamental genetics concepts aligning with the Next Generation Science Standards [30]. In Geniventure, students are faced with the challenge of correctly breeding and studying virtual drakes, a model species of dragon [13]. In order to successfully produce the desired drake for each in-game exercise, students are required to learn and explore genetics concepts such as heredity, dominant and recessive traits, and protein-to-trait relationships.

The game is comprised of 60 progressively difficult puzzle-like challenges that are divided into six distinct levels (Figure 1). Each level is divided into different in-game “missions”, and each mission is comprised of the individual challenges. The types of challenges presented to the student varies widely across the different levels. Geniventure is designed to be played in a linear sequence, but students are allowed to attempt any challenge at any time, and also have the freedom to quit any challenge prior to completion.

For the first three levels of Geniventure, students are faced with the task of modifying the genotype of a presented drake to match a target phenotype (Figure 1, Level 1). These challenges require the student to understand several different genetics concepts and also correctly predict attributes of the target phenotype based on the current genotype. To determine whether the student correctly completed the challenge or not, the student selects the “Check” or “Hatch” button in the game’s interface to submit their answer. At this point, the student receives binary feedback on whether the exercise was successfully completed or not. If the exercise was not successfully completed at this time, the student is presented with a hint to help reach completion. There are three hints available per exercise, with each hint becoming progressively more direct, a visual cue is also made available to the student at this time. The student is allowed to make additional changes and resubmit their proposed phenotype until the correct solution is reached, or until the student exits the exercise. The progressive hint mechanism exists for many exercises in Geniventure, although the structure and conceptual challenges in each exercise may vary widely. Level 2 further advances the challenge of matching a genotype to a specified phenotype by introducing dominant and recessive traits (Figure 1, Level 2), while Level 3 increases the complexity of the exercise by adding factors such as scale color, proteins, and cell modification (Figure 1, Level 3). Levels 4, 5, and 6 introduce increasingly complex concepts such as breeding, inheritance, and meiosis. Level 4 introduces more complexity to the breeding process through the use of gametes, epistasis, and more challenging inheritance patterns (Figure 1, Level 4). Level 5 presents students with the test cross concept, a genetic method for determine an organism’s genotype by crossing it with a fully recessive organism (Figure 1, Level 5). Level 6 builds on the prior concepts of the game while introducing additional concepts such as X-linked and polyallelic traits (Figure 1, Level 6). Certain levels introduce gameplay narratives or scaffolding that are not present in prior levels. For example, Level 3 uses a “pod-release gate” interface which varies from Level 4’s “Gamete Builder”, Level 5’s “Test Cross” interface, and Level 6’s “Clutch Breeder”. As a result, this may result in different problem-solving behavior distributions while labels for the new concepts are not available yet to train competency models and thus provides the motivation for investigating model generalization techniques such as domain adaptation or zero-shot learning.

Data Collection

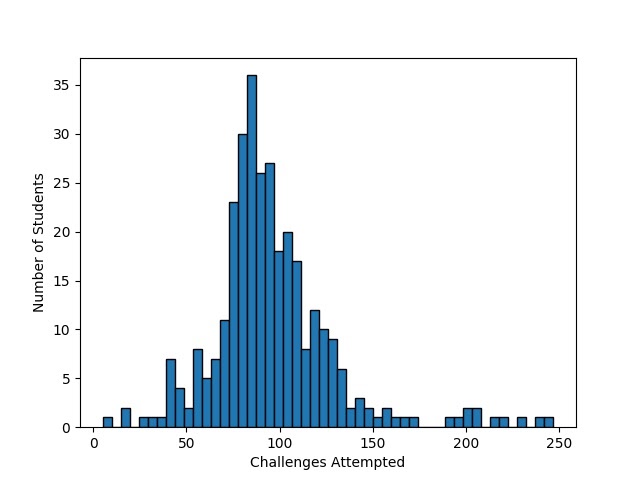
Following Institutional Review Board (IRB) approval, the data corpus was captured from 462 consenting students across seven high schools and a middle school located in the Eastern United States from suburban, rural, and urban locations. Teachers led several different classroom implementations of Geniventure where students engaged with the game during instruction periods across multiple days. Prior to the first learning session, students took a pre-test knowledge assessment consisting of 28 questions related to the genetics concepts presented in the game. Following the conclusion of the last learning sessions, students took an identical post-test knowledge assessment addressing the same concepts to quantify students’ learning gain. The knowledge assessment was aligned with Geniventure’s competency model based on the ECD formulation of the game, and the assessment was also validated through multiple rounds of expert review and cognitive interviews with students. The knowledge assessment’s administration showed an internal consistency reliability of alpha=.873, and both the pre- and post-test were administered through the same online platform as the game. Logistical and technical issues were encountered during the data collections, which resulted in 38 students being removed from the data corpus due to missing knowledge assessment data and 108 students being removed due to missing gameplay log data. As a result, the data corpus is comprised of gameplay log data from 316 students. Student performance on the post-test (M=19.33, SD=6.131) was shown to be a statistically significant improvement over the pre-test (M=14.41, SD=5.826) according to a paired t-test (t(316) = 14.663, p<.01, Cohen’s d=.823). The distribution of completed challenges per student appears to be relatively normal (Figure 2), with most students completing between 50-150 challenges, with a range of 5 to 248 challenges (M=95.89, SD=33.63).

Feature Engineering

Features representative of students’ gameplay were engineered from the raw timestamped log files generated for each learning session. These log files contained action-level information about students’ in-game activity, such as moves made within a challenge, number of attempts, and number of hints received. Because of the differences in gameplay mechanics across the different levels and challenges, we generated nine generic, challenge-level representations of student activity to generalize the feature engineering process. The generic representations were: (1) level number of challenge, (2) mission number of challenge, (3) challenge number, (4) total time spent on challenge, (5) number of in-game actions taken during challenge, (6) number of hints encountered during challenge, (7) number of correct in-game actions taken during challenge, (8) number of wrong in-game actions taken during challenge, and (9) student’s completion status of challenge (0: incomplete, 1: complete with wrong answer, 2: complete with correct answer). From these representations, we also generate additional features to capture the temporal context of students’ activity across current and prior learning sessions. By accounting for all student challenges completed up until the current challenge, we calculated: (10) average time spent on individual challenges (seconds), (11) average in-game movements per challenge, (12) average correct in-game movements per challenge, (13) average incorrect in-game movements per challenge, (14) average number of hints received per challenge, (15) successful challenge completion rate, (16) failed challenge completion rate, and (17) unsubmitted challenge rate. For each challenge, a feature vector was constructed using these 17 features to serve as the input to the student competency models. It should be noted that these averages were computed separately across the “seen” and “unseen” gameplay data to protect against data leakage.

Evidence-Centered Design

Stealth assessment refers to non-intrusive methods for collecting evidence to induce student competency models [38]. This evidence captured from student interactions with various learning platforms is subsequently used to inform the evidence models, and subsequently competency models. The competency predictions generated from these models can be used to enable enhanced learning through adaptive mechanisms within the learning platforms. Stealth assessment can also be used to inform teachers and instructors in real time about students’ current learning trajectories to determine if dynamic interventions are necessary.

Stealth assessment is grounded in Evidence-Centered Design (ECD), a principled approach to assessment design that describes high-level models of a conceptual assessment framework and delivery architecture for assessment delivery systems [27]. ECD affords assessment designers a method for reasoning about student knowledge or skills while adhering to psychometric principles [28]. Historically, ECD has been utilized to guide the creation of various knowledge assessments, and more recently has been used to inform the development of stealth assessment models deployed within game-based learning environments [14, 24, 37]. Our approach to stealth assessment with the Geniventure learning environment is informed by the three following ECD models:

Task Model: This model defines the exercises or activities that students attempt to complete through interactions with the game-based learning environment. The task model within Geniventure is comprised of sixty distinct challenges that are split across the six in-game levels. Each challenge presents students with various genetics concepts such as inheritance patterns, breeding, and genotype-phenotype relationships.

Evidence Model: This model is shaped by the actions performed by each student within the game-based learning environment. This interaction data is representative of student behavior that is correlated with learning outcomes pertaining to specific concepts presented in the learning platform. In this work, the actions a student performs in Geniventure challenges, in addition to the outcome of each challenge, are represented by the evidence model and used to engineer features to train machine learning models used for predicting student mastery (or no mastery) of particular genetics concepts. The evidence model guides the competency model as it adjusts its modeling of students’ competencies as various in-game challenges are attempted.

Competency Model: This model pertains to the genetics concepts that are presented within Geniventure and attempts to model the machine-interpretable evidence from the evidence model in order to accurately predict students’ competencies for each concept. The primary objective of the competency modeling is to optimally map the evidence model to the competency model for each student. These concepts are derived from classroom learning objectives and state science standards through of expert review. Students’ competencies are captured and quantified from a post-test knowledge assessment administered to each student following interactions with Geniventure. The competency model and the post-test assessment are aligned using the same concepts presented in Table 1.

To generate the ground-truth competency scores for each student, individual responses to the items on the post-test assessment are summed across the different genetics concepts, with a single concept mapping to between one and six questions on the assessment. Each question considered in this study is graded as either 1 (correct) or 0 (incorrect). Competency scores are calculated for each concept by dividing the total number of correct responses for that concept by the total number of questions related to that concept. As a result, each competency score was within the range of 0 to 1 and serves as the target variables for the stealth assessment models.

Zero-Shot learning

Zero shot learning (ZSL) is an extreme variation of unsupervised domain adaptation, which focuses on two distinct data sets extracted from two different domains and data distributions: a source domain and a target domain. The primary objective of unsupervised domain adaptation is to induce a generalizable model that is capable of accurately classifying samples from the two domains in instances where labels for samples in the target domain are not available during model training. However, ZSL expands on this concept by assuming that neither data samples nor labels for the target domain are available during the training process. For this work, we split the Geniventure dataset into seen (S) and unseen (U) domains by partitioning between in-game levels because different levels address concepts that correspond to different competencies according to the ECD model. The text descriptions of each ECD concept serve as the link between the seen and the unseen classes, commonly referred to in ZSL as “semantic embeddings” or “attribute vectors” and are known for both seen and unseen classes at training time. The seen domain serves as the “source” domain and the unseen domain serves as the “target” domain. Therefore, the ECD concepts (C) for this data corpus (X: data, Y: class labels) can be divided and formally defined as follows:

$S = \left\{ \left( x,\ y,\ c_{y} \right)\ |\ x \in X^{S},\ y \in Y^{S},\ c \in C^{S} \right\}$ (1)

$U = \left\{ \left( x,\ y,\ c_{y} \right)\ |\ x \in X^{U},\ y \in Y^{U},\ c \in C^{U} \right\}$ (2)

By framing the ECD competency modeling as a ZSL task, we seek to predict student competencies on unseen levels and concepts in situations where no prior gameplay data is available for those concepts, an example of the “cold-start problem”. For example, if we have concepts C1-C10 where C1-C7 have been previously presented to students in Geniventure and gameplay logs have been captured for these concepts (i.e., seen), we seek to use this available data to induce generalizable competency models that accurately predict student outcomes on concepts C8-C10, even though they have not been presented to any students and there is no prior gameplay logs or competency scores for these concepts (i.e., unseen). This allows for more generalizable student competency modeling and also enables ECD-based stealth assessment in circumstances where there are no prior ground-truth competency labels, such as when post-tests may be unavailable or impractical to administer. Examples include informal learning environments such as museums, or if a concept or level within a game-based learning environment is being deployed for the first time.

Because both the data and labels are not available at training time, a form of semantic data must be available for the ZSL framework to link between the seen and unseen domains. In this particular case, we use the text-based descriptions of each of the concepts to generate concept mastery embeddings used as conditional inputs to the generative ZSL models (Section 5.1). This allows the generative model to learn the non-linear relationships between the concept text embeddings, student competencies, and student gameplay patterns. As a result, the generative model generates synthetic gameplay data representative of each of the seen and unseen concepts which enhances the training and generalizability of the competency models.

The embedding representations for the genetics concept descriptions are generated using Sentence-BERT (S-BERT) [33]. S-BERT expands upon the original BERT model [10] by implementing the BERT model within a Siamese network architecture to facilitate the generation of fixed-length embedding vectors of sentences that are compared using distance metrics such as cosine similarity. This allows the S-BERT model to generate sentence-level embedding representations instead of single-word embeddings, making this model suitable for sentence descriptions of the genetics concepts. Additionally, the use of a common pre-trained language model such as S-BERT improves the generalizability of our approach, compared to manually crafted representations such as knowledge graphs.

Generative Modeling

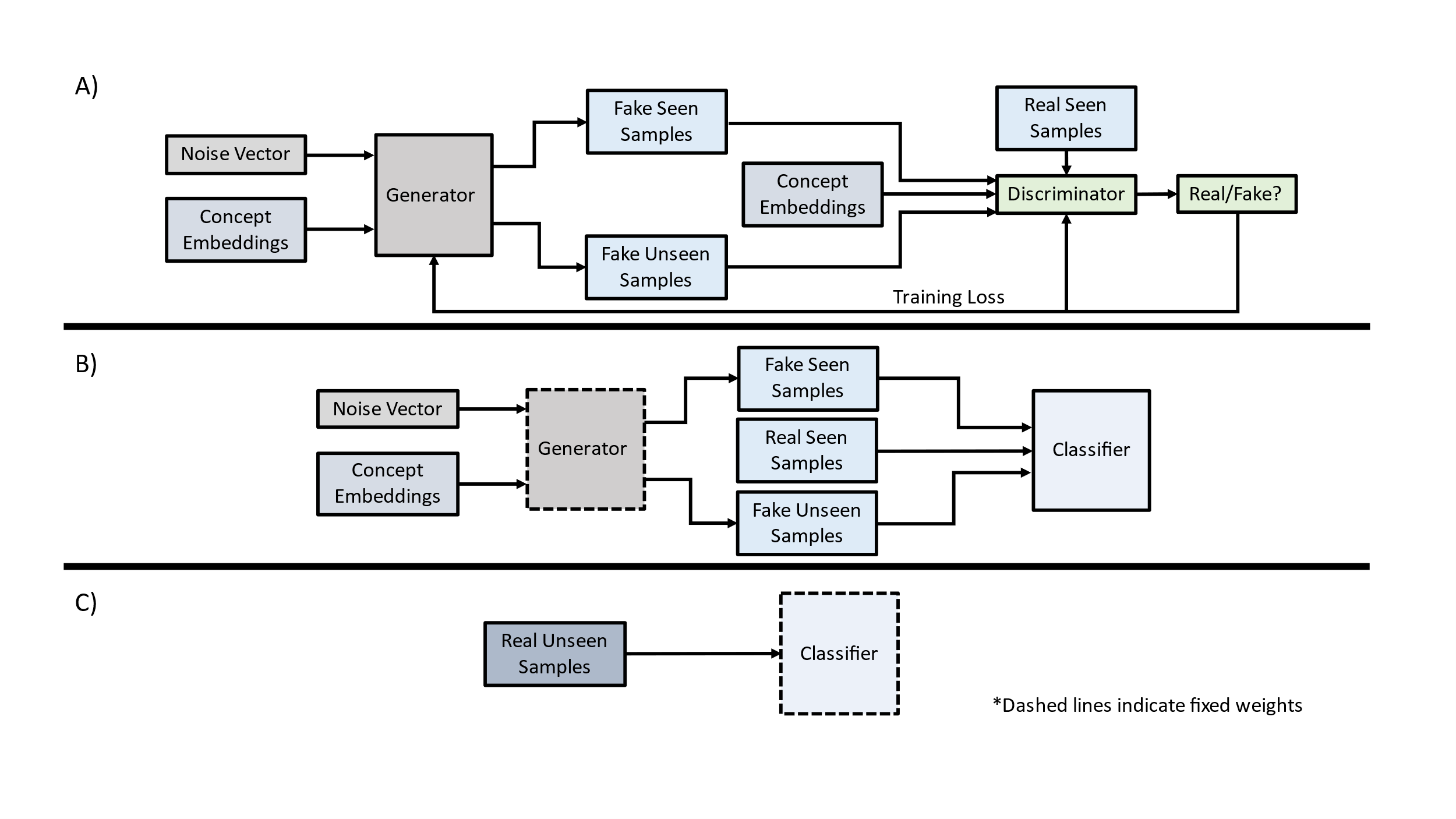
To address the absence of training data and labels for the unseen concepts, we use semantic data (i.e., text descriptions of all concepts) to condition and train deep generative models, which facilitate data augmentation for this task. By employing text embeddings of the seen concept descriptions to condition the generative models, we can train the models to map the latent representation of each concept to particular patterns and features in the students’ gameplay data for the seen concepts. We can subsequently generate synthetic data to represent student gameplay for the unseen concepts using only the embeddings of the descriptions for each unseen concept. The augmented data is used to further train the competency models to increase the predictive performance during inference for the unseen concepts’ associated gameplay data.

Generative adversarial networks (GANs) have been frequently used as a data augmentation method due to their ability to generate high-fidelity data from noise vectors through zero-sum training of two deep learning components: a generator and a discriminator [15]. The purpose of the generator G is to generate synthetic data $\widetilde{x}\$based on a random probability distribution p_z, where z represents the latent space sampled by G so that $\widetilde{x}$ = G(z), z ~ p_z. The objective is that $\widetilde{x}$ deceives the discriminator, whose purpose is to accurately distinguish between this “fake” data and real samples from the original data. The discriminator’s training loss from this binary classification is backpropagated through the generator and the discriminator, with the objective of both losses eventually reaching a Nash equilibrium. However, quantifying GAN convergence is an open-ended area of research and GAN models are often susceptible to vanishing or exploding gradients, mode collapse, and other instabilities during the training process. One approach to mitigating this issue is a conditional GAN [25], which extends a traditional GAN architecture by providing associated data (“conditions”) to both the generator and discriminator’s input vectors. An example of such a condition is a class label or attribute that is associated with the desired augmented output of the generator. For this particular case, we use the S-BERT embedding vectors of the associated concepts as the conditions to our GAN model to generate synthetic gameplay data associated with both the seen and unseen concepts.

Traditional GAN architectures attempt to reach convergence by minimizing a divergence function such as the Jensen-Shannon (JS) divergence, which helps quantify the distances between two probability distributions p_g(x) and p_r(x), where p_g is the model distribution of the generator and p_r is the distribution of the real data. However, a common issue with these divergence metrics is that there exist sequences of distributions that do not converge under the JS divergence or where the gradient of the divergency eventually disappears, effectively halting the training of the generator during backpropagation. To address this issue, an alternative GAN architecture (W-GAN) was proposed that utilizes the Wasserstein distance, otherwise known as the “Earth Mover’s distance”, as a means to quantify the generator loss during training (Eq. 3) [2]. This metric is desirable as it is continuous and differential almost everywhere under the Lipschitz condition:

$W\left( p_{r},\ p_{g} \right) = \ \inf_{\gamma \in \sqcap (p_{r},\ p_{g})}{\mathbb{E}_{\left( x,y \right)\sim y}\lbrack \parallel x - y \parallel \rbrack}$ (3)

where $\sqcap (p_{r},\ p_{g})$ represents all joint distributions with marginal distributions of $\gamma$(x, y) are $p_{r}\left( x \right)$ and $p_{g}(y)$, respectively. Because this equation is highly intractable, we use the Kantorovich-
Rubinstein duality to simplify the calculation to be:

$W\left( p_{r},\ p_{g} \right) = \ \sup_{{|f|}_{L} \leq 1}{\mathbb{E}_{x\sim p_{r}}\left\lbrack f\left( x \right) \right\rbrack - \mathbb{E}_{x\sim p_{g}}\left\lbrack f\left( x \right) \right\rbrack}$ (4)

As a result, we enforce a 1-Lipschitz constraint to the discriminator component. As a means to enforce this 1-Lipschitz constraint within the W-GAN, we introduce a concept known as “weight clipping” to the discriminator. This involves constraining the weights in the discriminator to be between the range of [-c, c], with c being treated as an additional training hyperparameter. However, weight clipping is often volatile with respect to c and can cause W-GANs to converge much more slowly if c is too large but can also introduce vanishing gradients if c is too small. An alternative to the weight clipping is a “gradient penalization” method which proposes a penalty term added to the loss function that is parameterized by a penalty coefficient λ [17]. The gradient penalty term is based on weighted random sampling between the real and the generated samples from the generator. As a result, the final objective of our gradient-penalized W-GAN model (WGAN-GP) becomes the minimization of the following loss function for the discriminator D:

$$\mathcal{L}_{\text{dis}}\left( x,\widetilde{x};\theta_{\text{dis}} \right) = \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$$

$\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ D}_{\theta_{\text{dis}}}\left( \widetilde{x} \right) - D_{\theta_{\text{dis}}}\left( x \right) + {\lambda( \parallel \nabla_{\widetilde{x}}D_{\theta_{\text{dis}}}\left( \widehat{x} \right) \parallel - 1)}^{2}$ (5)

where $\theta_{\text{dis}}$ represents the parameters of the discriminator, $\lambda$ is the gradient penalty coefficient, and $\widehat{x}$ is sampled from $\epsilon x + \left( 1 - \epsilon \right)\widetilde{x}$ with 0$\leq \epsilon \leq 1$, effectively representing any points sampled between the probability distributions, p_g and p_r.

We employ the WGAN-GP approach as a means to train a generator to produce realistic synthetic data representing students’ gameplay for unseen Geniventure levels in order to induce student competency models for the associated genetics concepts that have not been previously introduced. This model was selected due to issues with vanishing gradients during empirical evaluations of traditional GANs and WGANs within our ZSL framework. Additionally, we use a conditional variation of the WGAN-GP model in order to effectively map the latent representations of the augmented data representations to the word embeddings of the text-based descriptions of each genetics concept. This allows the synthetic data generation to be guided by the concepts associated with each data sample from the data corpus, while allowing for data to be generated based on the concepts associated with the unseen game levels.

methodology

Our ZSL approach is evaluated across two different data splits. The first split involves removing any information from the ECD models associated with Level 6 (the last level) from the data corpus, which includes student gameplay (Evidence Model) from the challenges within the level (Task Model), as well as the student post-test scores (Competency Model) to items associated with genetics concepts associated with Level 6 (C13 and C14 serving as unseen concepts). The second split involves treating Level 5 and Level 6 as the “unseen” domain, which involves concepts C7, C13, and C14. The competency models are initially trained using the student gameplay features from the “seen” domain and a median split of the combined competency scores from the post-test items corresponding only to concepts associated with the “seen” Geniventure levels. To evaluate the ZSL performance, each competency model is evaluated using the gameplay from the unseen levels to predict student competencies from the post-survey items associated with the unseen concepts. This process is implemented to protect against data leakage, ensuring that the student competency models are induced using only data and labels from the seen levels as well as unseen, synthetic labeled data during the training phase, and any actual data or labels from the unseen concepts and levels are only presented to each competency model during the inference phase (Figure 3, C).

Student Competency Models

Five different classifiers were investigated as student competency models: a majority classifier, support vector machine (SVM), random forest (RF), Naïve Bayes (NB), logistic regression (LR), and feedforward neural network (FFNN). Each of the models were implemented as binary classifiers to predict “high” and “low” categories of student performance based on a median split of the sum of the post-test score for each question related to either the seen or unseen concepts. Each of the models was evaluated using student-level cross-validation, to ensure against data leakage across validation folds. The median of the competency scores were determined based on the scores of the students within the training folds only as another means to protect against data leakage.

Model Evaluation

Hyperparameter tuning was performed using three-fold inner cross-validation within each iteration of the ten-fold outer cross-validation. The hyperparameters that were optimized were the regularization parameter and kernel (support vector machine; SVM), regularization parameter (logistic regression, LR), number of estimators (random forest; RF), and number of layers and nodes (feedforward neural network; FFNN). Hyperparameter tuning was not performed on the Naïve Bayes classifier and the majority classifier. Because multiple data samples exist per student and there is only one competency label per student, we generate a single student-level prediction by forward propagating all feature vectors for a given student through a trained competency model and averaging across all predictions for that student.

Because the use of the gradient penalty in the WGAN-GP stabilizes the training process and mitigates the need for extensive hyperparameter tuning, we focus only on tuning the number of nodes in the two hidden layers of the generator and discriminator using layer sizes of 32 or 64. This hyperparameter tuning also occurred within the nested cross-validation process described previously. The WGAN-GP’s learning rate was 0.001, with a dropout rate of 0.5 and hyperbolic tangential activation functions. The WGAN-GP (and FFNN competency model) was trained using 100 epochs while utilizing early stopping based on the model’s performance on the validation fold with a patience of 10 epochs. The noise vector size for the WGAN-GP was 32, and the number of generated synthetic data samples was set to be 50% of the original training dataset size. Because the concept mastery embedding vectors obtained from S-BERT are high in dimensionality, we perform Principal Component Analysis on the embeddings to reduce the size to 32 components. The data was standardized within each cross-validation fold by subtracting each feature’s mean and dividing by the standard deviation of each feature as determined by the training folds.

To represent the students’ competencies within the semantic embeddings, a text description for each concept was preceded with either “mastery of” or “no mastery of” based on each student’s post-test performance relative to the median for each concept and these substrings were concatenated together to form a single comprehensive text string representing the student’s mastery of each of the seen concepts. For example, a concept mastery sentence for a single student might be “Mastery of only one dominant allele is needed to produce the dominant trait. Non-mastery of two recessive alleles are needed to produce a recessive trait. Mastery of …” and so on for the seen concepts. These text representations are then passed through the pre-trained S-BERT word embedding model and, following the PCA dimensionality reduction described previously, are used as the conditional features for the generative models. To generate synthetic data following the generative model training, a similar process is followed to generate the text representations using the descriptions of the unseen concepts. As no student competency data actually exists for these unseen concepts currently, the preceding phrase “mastery of” or “no mastery of” is determined using a Bernoulli probability distribution where probability p=0.5. This allows the generative model to produce synthetic gameplay data representative of many possible mastery/non-mastery combinations of student competencies for the unseen concepts, thus enhancing the generalizability of the competency models for the unseen concepts.

To evaluate the performance of the WGAN-GP as the preferred ZSL generative model, we also investigate two alternatives: a conditional variational autoencoder (C-VAE) and a “target-only” baseline. The target-only baseline refers to a competency model that performs the inference on the data for the unseen Geniventure levels but does not undergo any form of ZSL-based data augmentation, which is a reflection of the target-only baseline in prior adversarial domain adaptation work by Tzeng et al. [43]. C-VAEs are similar to conditional GANs with regards to the use of conditional attributes [39]. A traditional VAE contains two components: an encoder and a decoder. The encoder learns latent representations of input data while the decoder seeks to reconstruct the original dimensionality of the data from the latent space representation. The VAE constrains the latent space representation to follow a pre-determined probability distribution by minimizing a loss function that consists of a reconstruction term and a divergence term. The reconstruction term quantifies the reconstruction error of the decoder component through a loss function such as root mean squared error and the divergence term quantifies the distance between the given probability distribution and the latent representation distribution. The Kullback-Leibler (KL) divergence is often used for this purpose. The conditional features are concatenated to the input features for the encoder as well as the latent representation vector that is passed from the encoder to the decoder. Because the encoder reduces the latent representation to a parameterized probability distribution, this allows the decoder to generate augmented data from this distribution.

Results and discussion

The ZSL approach was evaluated across two splits as described in Section 5. The results for Split 1 is shown in Table 2, while the results for Split 2 is shown in Table 3. We select F1 Score and accuracy as our primary metrics to account for the relatively balanced class distribution due to the median split, while Area-Under-Curve (AUC) and Cohen’s Kappa [8] are used as secondary metrics. The optimally performing generative ZSL model for each split in terms of F1 Score is shown in bold. All evaluations were performed on a NVIDIA GeForce GTA 1080 TI GPU. Each evaluation took up to 100 minutes to compete the 10-fold cross-validation sequence.

In terms of the primary evaluation metrics, the WGAN-GP model appeared to induce the highest performance from the competency models across both data splits, outperforming both the C-VAE and the target-only baseline. It was noted that the performance across all models decreased for the split containing two “unseen” gameplay levels (Table 3) compared to one (Table 2), which is expected due to the decrease in training data available as well as the increased variance in the “unseen” dataset. However, the results overall point to the enhanced performance of the student competency models when additional synthetic data is generated from the WGAN-GP as a means to improve the training process.

Additionally, it was noticeable that the margin between the WGAN-GP and the other ZSL configurations widened from Split 1 to Split 2, which points to the relative scalability of our approach as the number of unseen concepts and in-game levels increase. It was also noted that the C-VAE was the lowest performing generative model and was also outperformed by the target-only baseline approach for both data splits. This is noteworthy as VAEs, including conditional variations, are the generative approach for prior generalized ZSL work [26, 44, 45].

However, we note in these prior works, the VAE models were trained on a multimodal dataset, which provides a more data-rich perspective compared to the stealth assessment data in this work. Additionally, although the work in [26] used a conditional variation of the C-VAE, the generative model appeared to suffer from mode collapse, a common issue in the training of generative models. However, one benefit of the WGAN (and the gradient-penalization modification) is additional mitigation against mode collapse during training, a possible explanation of why the WGAN-GP achieves the highest performance in our evaluations. A primary difference in this architecture is that the loss of the decoder in the C-VAE is the summation of the KL divergence and the reconstruction loss, compared to the WGAN component which strictly uses the Wasserstein divergence metric. This has potential for allowing the generative model to map between the semantic feature space and the augmented data more effectively, particularly as the augmented data from the WGAN-GP is restored to the original dimensionality instead of a latent space representation.

To further investigate the performance of the generative ZSL approach, we generate the confusion matrices for each of the models across both data splits (Figures 4 and 5). The confusion matrices are based on the inferences of each of the models based on the held-out test set within each outer cross-validation iteration, for a total of 316 student-level predictions. It should be noted that the results in Tables 2 and 3 were calculated across the outer cross-validation folds while the analyses conducted in Figures 4-7 were calculated across the entire dataset. Based on the results in the confusion matrices, we observe that high-performing students are more accurately classified compared to low-performing students. Additionally, it appears that the student competency models produced noticeably more false negatives as the unseen concepts increased. This occurred across all three evaluated ZSL approaches. In the case of the target-only baseline and the WGAN-GP model, the student competency models were able to retain a relatively similar

performance for correct identification of low-performing students across both data splits, but the C-VAE led to significantly decreased detection for low-performing students when evaluating from Split 1 to Split 2. Additionally, it is noticeable that the WGAN-GP was able to maintain relatively consistent performance for prediction of both high-performing and low-performing students across both data splits, which demonstrates the generalizability of this particular generative model.

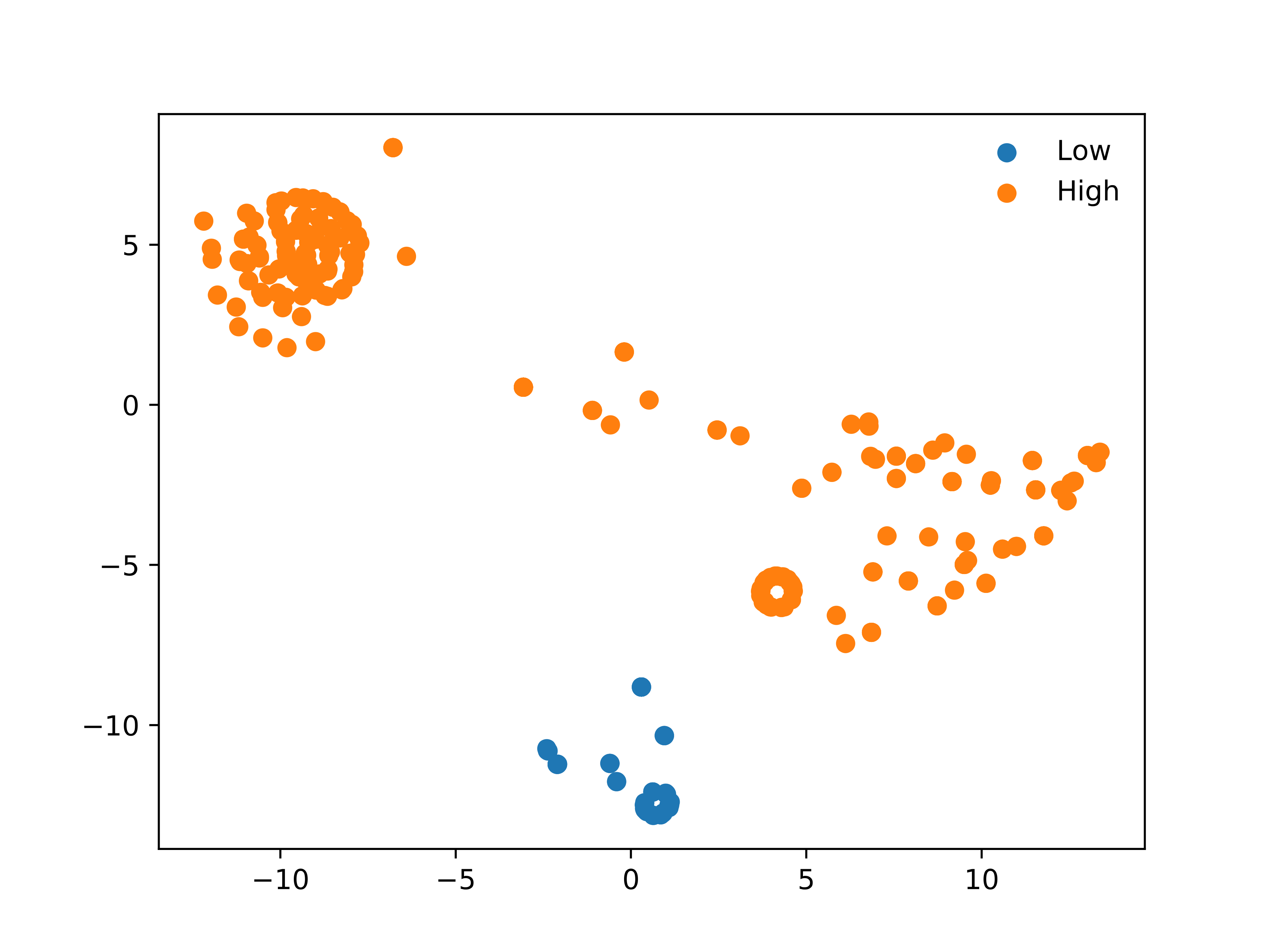
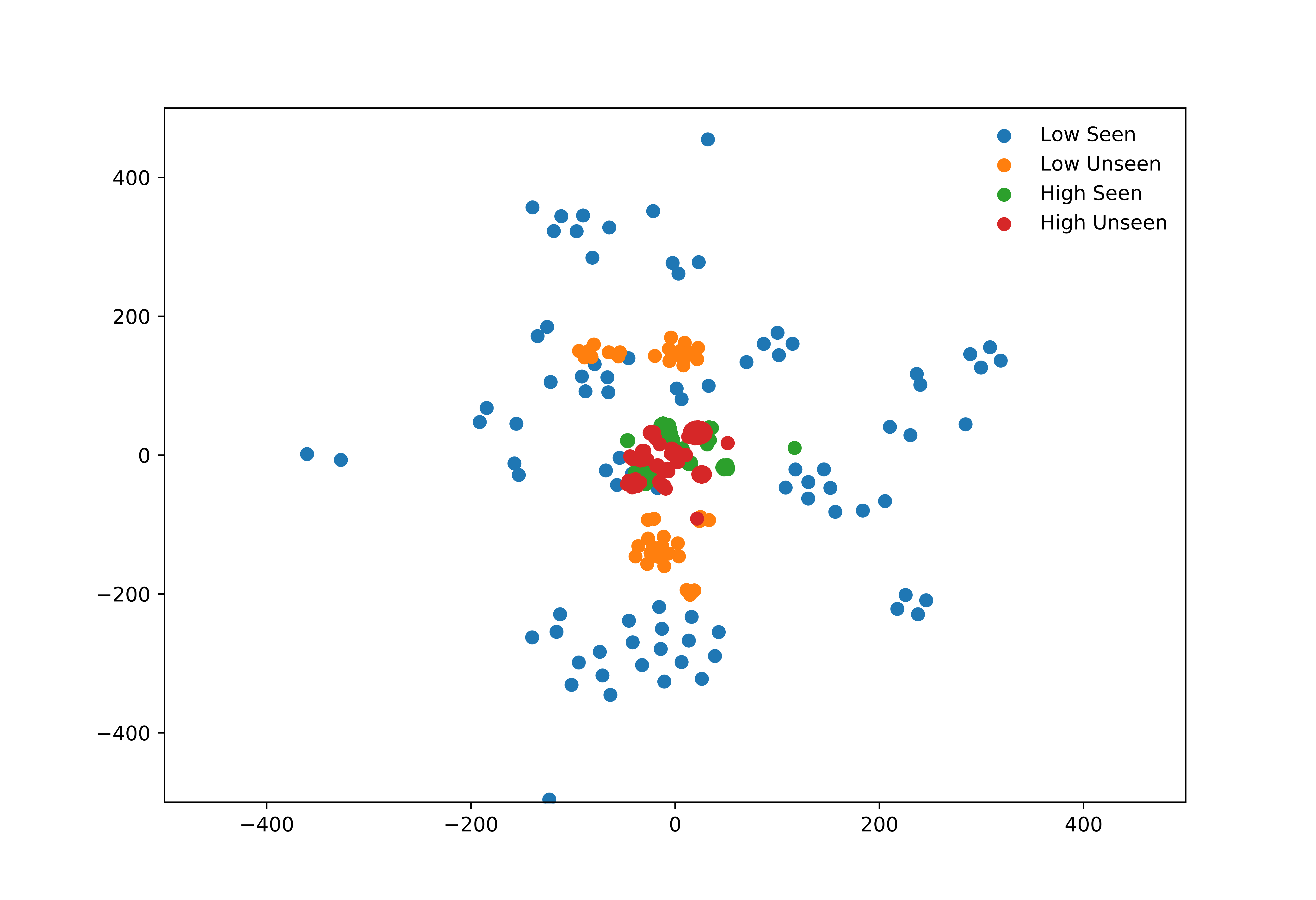
To further evaluate the predictive value of the semantic embeddings of the student competencies with the various genetics concepts, we visualize the embeddings from each of the students using the principal components generated from the S-BERT embeddings. Using the t-distributed Stochastic Neighbor Embedding (t-SNE) plots for the low-performing and high-performing students (Figure 6), we are able to detect whether there are salient or underlying predictive patterns in the text representations of each student’s mastery of individual genetics concepts. Despite the use of PCA for dimensionality reduction for the original S-BERT embeddings, the representations of the semantic embeddings contain high dimensionality and thus poses a challenge for visualization. t-SNE attempts to address this issue by producing a representation of high-dimensionality data within 2D coordinate space. This is performed by constructing joint probability distributions to model the similarity between the original data points, and subsequently attempts to minimize the KL divergence between these probability distributions and other probability distributions within 2D coordinate space. This process is expanded to distinguish between low-performing and high-performing students for the seen and unseen concepts (Figure 7). Figures 6 and 7 are generated using Split 2.

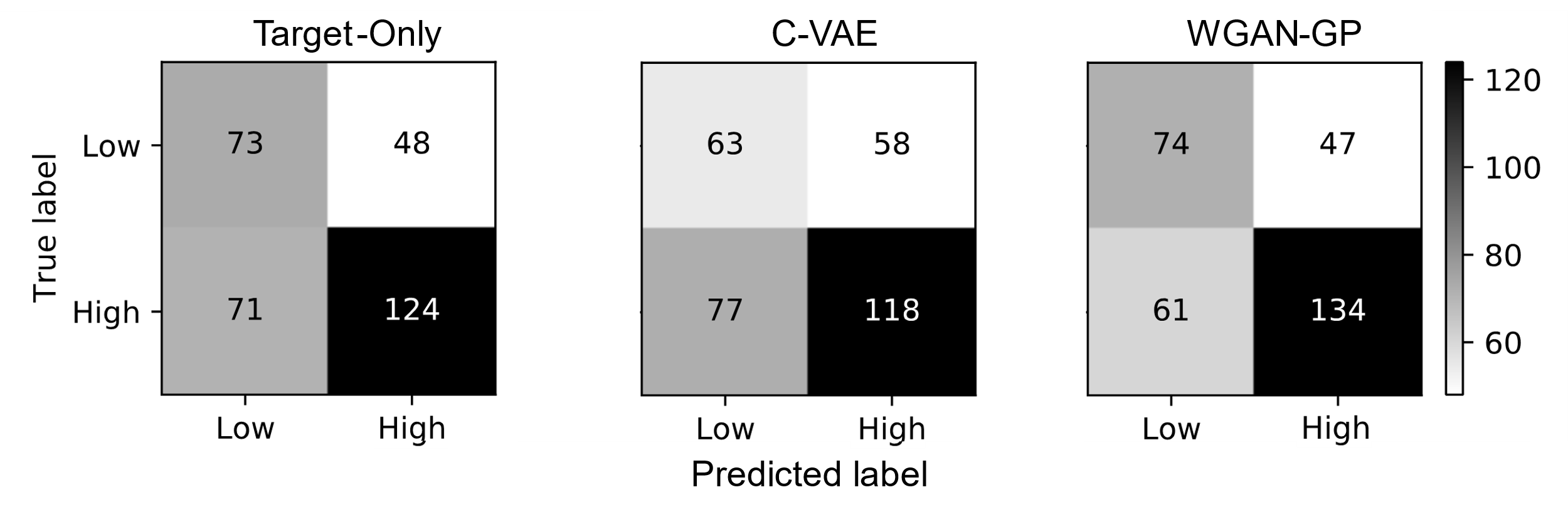
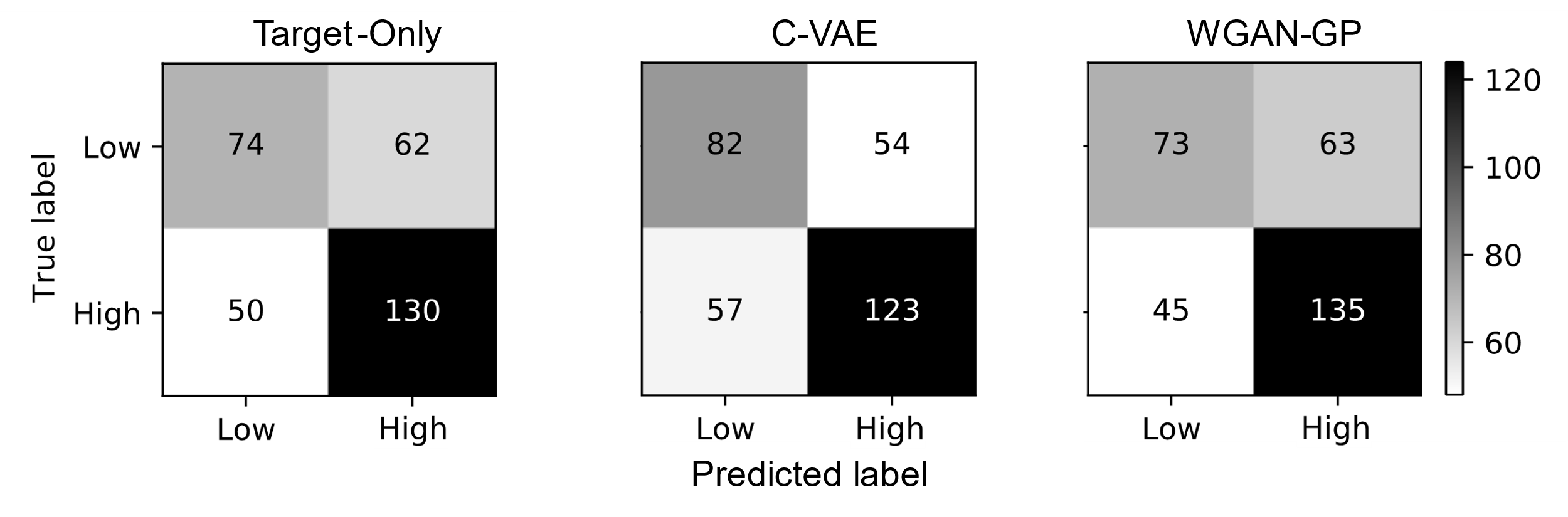
Figure 6 indicates that the use of semantic embedding representation of the students’ masteries of various genetics concepts may provide predictive context to the generative ZSL models when used as a conditioning input during training. Noticeably, there appears to be distinct separation between the semantic embeddings for high-performing students and low-performing students when calculated using all competencies, which points to the predictive value of using these embeddings for stealth assessment tasks. To provide analysis more similar to the ZSL framework, the semantic embeddings are generated for each group of low-performing and high-performing students by separating the embeddings for seen and unseen concepts (Figure 7). In this particular case, there appears to be notable separation between clusters of low-performing students and high-performing students, with overlap between the high-performing students across both seen and unseen concepts. As a result, this indicates that the use of the semantic embeddings alongside conditional generative modeling provides additional predictive value to guide the generation of augmented data for different students based on prior competencies. One aspect of note for Figure 7 is that the plots of “High Unseen” and “Low Unseen” are based on the ground-truth competencies for the students on the unseen concepts, while in practice, this data is not available for training the stealth assessment models and the semantic representations are used by assigning “high” or “low” mastery of each concept at random and then generating a synthetic binary “label” based on whether at least 50% of the unseen concepts were labeled “high” or not. This allows the generative model to be conditioned on 2ⁿ different combinations of student concept mastery where n is the total number of unseen concepts, and this allows the model to be trained using a higher number of mastery combinations than what is often available in datasets captured from game-based learning environments.

There are limitations to this work that should be noted. Although the zero-shot learning framework was based on seen and unseen domains across differing gameplay levels, the two domains were grounded in the same game-based learning environment. To further investigate the generalizability of the ZSL framework, our approach should be evaluated using unseen data and classes from entirely different learning environments. Additionally, Split 1 and 2 removed two and three concepts out of sixteen, resulting in 12-18% of the total data being treated as unseen data. Evaluations with more unseen in-game levels would provide more insight into the performance of our approach as the unseen domain increases. The class label for the seen and unseen domains were both based on binary labels of student mastery, but our method should also be evaluated in scenarios where the labels differ more widely (e.g., an additional unseen class in multi-class prediction). The binary labels were utilized to convert our work to a classification task, but the level of granularity is much higher compared to regression, which can negatively impact the adaptability of learner-sensitive mechanisms by grouping low-performing students and students performing near the median together. It was also noted that, as the unseen domain increased, the number of false negatives increased, which could lead to high-performing students receiving unnecessary interventions in user-adaptive settings.

conclusion

Game-based learning holds significant potential for stealth assessment of student performance and knowledge acquisition. The capability to predict student mastery of particular concepts within game-based learning environments can enable mechanisms such as adaptive hint generation, personalized gameplay narratives and scaffolding, and gameplay-sensitive interventions in real-time. However, stealth assessment models often necessitate large amounts of data and labels, which presents logistical and scalability challenges. This prohibits the deployment of pre-trained stealth assessment models in domains where prior data and labels have not been collected, and questions remain regarding generalizability to different domains and educational content.

We propose a generative zero-shot learning framework to address the above issues. By using conditional generative models, we harness the predictive capabilities of textual representations of student mastery of different educational concepts. These representations are able to guide a Wasserstein Generative Adversarial Network in generating synthetic student gameplay data representative of in-game levels and genetics concepts that have not been previously presented and for which no prior gameplay data or student competency data actually exists. By mapping text embeddings of genetics concepts to the student gameplay data through the generative model, the resulting augmented data improves the predictive capacity of stealth assessment models for predicting student competency across different hidden gameplay levels. Our proposed model is shown to outperform an alternative conditional generative model and a baseline that excludes the zero-shot learning element. This indicates the potential for increasing the generalizability of student stealth assessment models through the generative data augmentation approach and for deploying pre-trained stealth assessment models in digital learning environments presenting new educational concepts, problem-solving tasks, and in-game levels.

There are many promising avenues for future work. Notably, our work focuses on zero-shot learning within a single game-based learning environment, and the natural extension of this work is the evaluation of our framework across different learning environments instead of separate in-game levels. Additional experimentation with a higher ratio of “unseen”-to-“seen” concepts would provide more insight into how the ZSL framework’s performance is maintained as the amount of “unseen” data increases in size and variance. More complex modeling for the stealth assessment, language embeddings, and generative models may provide additional benefit for the predictive capacity of our framework. Finally, the effectiveness of our approach should be implemented alongside student-adaptive interventions to determine the impact on learning outcomes and processes within run-time environments.

ACKNOWLEDGMENTS

The authors would like to thank Robert Taylor for his assistance in facilitating this research. This research was supported by the National Science Foundation under Grant DRL-1503311. Any opinions, findings, and conclusions expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.

REFERENCES

1. Akram, B., Min, W., Wiebe, E., Mott, B., Boyer, K. and Lester, J. 2018. Improving stealth assessment in game-based learning with LSTM-based analytics. In Proceedings of the 11th International Conference on Educational Data Mining, 208–218.
2. Arjovsky, M., Chintala, S. and Bottou, L. 2017. Wasserstein GAN. arXiv:1701.07875.
3. Asbell-Clarke, J., Rowe, E. and Terc, E. 2013. Working through impulse: Assessment of emergent learning in a physics game. Games + Learning + Society. 9, 1, 1–7.
4. Binkley, M., Erstad, O., Herman, J., Raizen, S., Ripley, M., Miller-Ricci, M. and Rumble, M. 2012. Defining Twenty-First Century Skills. Assessment and Teaching of 21st Century Skills.
5. Chaudhry, R., Singh, H., Dogga, P. and Saini, S. 2018. Modeling hint-taking behavior and knowledge state of students with multi-task learning. In Proceedings of The 11th International Conference on Educational Data Mining, 21–31.
6. Cheng, M.-T., Rosenheck, L., Lin, C.-Y. and Klopfer, E. 2017. Analyzing gameplay data to inform feedback loops in The Radix Endeavor. Computers & Education. 111, 60–73.
7. Clark, D., Tanner-Smith, E. and Killingsworth, S. 2016. Digital games, design, and learning: A systematic review and meta-analysis. Review of Educational Research. 86, 1, 79–122.
8. Cohen, J. 1960. A coefficient of agreement for nominal scales. Educational and Psychological Measurement. 20, 1, 37–46.
9. Delacruz, G., Chung, G. and Baker, E. 2010. Validity Evidence for Games as Assessment Environments. National Center for Research on Evaluation, Standards, and Student Testing.
10. Devlin, J., Chang, M.-W., Lee, K. and Toutanova, K. 2019. BERT: Pre-training of deep bidirectional transformers for language understanding. arXiv:1810.04805.
11. Efremov, A., Ghosh, A. and Singla, A. 2020. Zero-shot learning of hint policy via reinforcement learning and program synthesis. In Proceedings of The 13th International Conference on Educational Data Mining, 338–394.
12. Falakmasir, M., Gonzalez-Brenes, J., Gordon, G. and DiCerbo, K. 2016. A data-driven approach for inferring student proficiency from game activity logs. In Proceedings of the Third ACM Conference on Learning @ Scale, 341–349.
13. McElroy-Brown, K. and Reichsman, F. 2019. Genetics with dragons: Using an online learning environment to help students achieve a multilevel understanding of genetics. Retrieved from http://concord.org.
14. Georgiadis, K., van Lankveld, G., Bahreini, K. and Westera, W. 2021. On the robustness of stealth assessment. IEEE Transactions on Games. 13, 2, 180–192.
15. Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A. and Bengio, Y. 2014. Generative adversarial networks. In Advances in neural information processing systems. 27, 1, 1–9.
16. Greipl, S., Moeller, K. and Ninaus, M. 2020. Potential and limits of game-based learning. International Journal of Technology Enhanced Learning. 12, 4, 1–45.
17. Gulrajani, I., Ahmed, F., Arjovsky, M., Dumoulin, V. and Courville, A. 2017. Improved Training of Wasserstein GANs. arXiv:1704.00028.
18. Henderson, N., Kumaran, V., Min, W., Mott, B., Wu, Z., Boulden, D., Lord, T., Reichsman, F., Dorsey, C., Wiebe, E. and Lester, J. 2020. Enhancing student competency models for game-based learning with a hybrid stealth assessment framework. In Proceedings of the 13th International Conference on Educational Data Mining, 92–103.
19. Hsiao, H.-S., Chang, C.-S., Lin, C.-Y. and Hu, P.-M. 2014. Development of children’s creativity and manual skills within digital game-based learning environment. Journal of Computer Assisted Learning. 30, 4, 377–395.
20. Hutt, S., Ocumpaugh, J., Biswas, G. and Baker, R.S. 2021. Investigating SMART models of self-regulation and their impact on learning. In Proceedings of The 14th International Conference on Educational Data Mining, 580–587.
21. Jesus, Â.M. de and Silveira, I.F. 2019. A collaborative game-based learning framework to improve computational thinking skills. In Proceedings of The 2019 International Conference on Virtual Reality and Visualization, 161–166.
22. Junokas, M.J., Lindgren, R., Kang, J. and Morphew, J.W. 2018. Enhancing multimodal learning through personalized gesture recognition. Journal of Computer Assisted Learning. 34, 4, 350–357.
23. Larochelle, H., Erhan, D. and Bengio, Y. 2008. Zero-data learning of new tasks. In Proceedings of the Twenty-Third AAAI Conference on Artificial Intelligence, 646–651.
24. Min, W., Frankosky, M., Mott, B., Rowe, J., Smith, A., Wiebe, E., Boyer, K. and Lester, J. 2020. DeepStealth: Game-based learning stealth assessment with deep neural networks. IEEE Transactions on Learning Technologies. 13, 2, 312–325.
25. Mirza, M. and Osindero, S. 2014. Conditional generative adversarial nets. arXiv:1411.1784.
26. Mishra, A., Reddy, S., Mittal, A. and Murthy, H. 2018. A generative model for zero shot learning using conditional variational autoencoders. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, 2188–2196.
27. Mislevy, R., Almond, R. and Lukas, J. 2003. A Brief Introduction to Evidence-Centered Design. ETS Research Report Series. 2003, 1, 1–29.
28. Mislevy, R., Behrens, J., DiCerbo, K. and Levy, R. 2012. Design and discovery in educational assessment: Evidence-centered design, psychometrics, and educational data mining. Journal of Educational Data Mining. 4, 1, 11–48.
29. Missaoui, S. and Maalel, A. 2021. Student’s profile modeling in an adaptive gamified learning environment. Education and Information Technologies. 26, 5, 6367–6381.
30. NGSS Lead States 2013. Next Generation Science Standards: For States, By States. The National Academies Press.
31. Nguyen, H., Hou, X. and Stamper, J. 2020. Moving beyond test scores: Analyzing the effectiveness of a digital learning game through learning analytics. In Proceedings of The 13th International Conference on Educational Data Mining, 487–495.
32. Oliveira, W., Isotani, S., Pastushenko, O., Hruška, T. and Hamari, J. 2021. Modeling students’ flow experience through data logs in gamified educational systems. In Proceedings of the 2021 International Conference on Advanced Learning Technologies (ICALT), 97–101.
33. Reimers, N. and Gurevych, I. 2019. Sentence-BERT: Sentence embeddings using siamese BERT-networks. arXiv:1908.10084.
34. Sabourin, J., Rowe, J., Mott, B. and Lester, J. 2013. Considering alternate futures to classify off-task behavior as emotion self-regulation: A supervised learning approach. Journal of Educational Data Mining. 5, 1, 9–38.
35. Shute, V., Ke, F. and Wang, L. 2017. Assessment and Adaptation in Games. Instructional Techniques to Facilitate Learning and Motivation of Serious Games. P. Wouters and H. van Oostendorp, eds. Springer International Publishing. 59–78.
36. Shute, V. and Rahimi, S. 2021. Stealth assessment of creativity in a physics video game. Computers in Human Behavior. 116, 1–13.
37. Shute, V., Rahimi, S., Smith, G., Ke, F., Almond, R., Dai, C., Kuba, R., Liu, Z., Yang, X. and Sun, C. 2021. Maximizing learning without sacrificing the fun: Stealth assessment, adaptivity and learning supports in educational games. Journal of Computer Assisted Learning. 37, 1, 127–141.
38. Shute, V. and Ventura, M. 2013. Stealth Assessment: Measuring and Supporting Learning in Video Games. The MIT Press.
39. Sohn, K., Lee, H. and Yan, X. 2015. Learning structured output representation using deep conditional generative models. In Advances in Neural Information Processing Systems, 2241–2251.
40. Spaulding, S., Shen, J., Park, H. and Breazeal, C. 2021. Towards transferrable personalized student models in educational games. In Proceedings of the 20th International Conference on Autonomous Agents and MultiAgent Systems, 1245–1253.
41. Talandron, M.., Rodrigo, Ma. and Beck, J. 2017. Modeling the incubation effect among students playing an educational game for physics. In Proceedings of the 18th International Conference on Artificial Intelligence in Education, 371–380.
42. Taub, M., Azevedo, R., Bradbury, A., Millar, G. and Lester, J. 2018. Using sequence mining to reveal the efficiency in scientific reasoning during STEM learning with a game-based learning environment. Learning and Instruction. 54, 93–103.
43. Tzeng, E., Hoffman, J., Saenko, K. and Darrell, T. 2017. Adversarial discriminative domain adaptation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 7167–7176.
44. Verma, V., Mishra, A., Pandey, A., Murthy, H. and Rai, P. 2021. Towards zero-shot learning with fewer seen class examples. In Proceedings of the 2021 IEEE Winter Conference on Applications of Computer Vision (WACV), 2241–2251.
45. Wu, M., Mosse, M., Goodman, N. and Piech, C. 2019. Zero shot learning for code education: Rubric sampling with deep learning inference. In Proceedings of the 33rd AAAI Conference on Artificial Intelligence, 782–790.
46. Zhang, J., Das, R., Baker, R. and Scruggs, R. 2021. Knowledge tracing models’ predictive performance when a student starts a skill. In Proceedings of The 14th International Conference on Educational Data Mining, 625–629.

© 2022 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.