ABSTRACT
Deep generative models with a specific variational autoencoding structure are capable of estimating parameters for the multidimensional logistic 2-parameter (ML2P) model in item response theory. In this work, we incorporated Q-matrix and variational autoencoder (VAE) to estimate item parameters with correlated and independent latent abilities, and we validate Q-matrix via the root mean square error (RMSE), bias, correlation, and AIC and BIC test score. The incorporation of a non-identity covariance matrix in a VAE requires a novel VAE architecture, which can be utilized in applications outside of education such as players performance evaluation, clinical trials assessment. Moreover, results show that the ML2P-VAE method is capable of estimating parameters and validating Q-matrix for models with a large number of latent variables with low computational cost, whereas traditional methods are infeasible for data with high-dimensional latent traits.
Keywords
1. INTRODUCTION
Item Response Theory (IRT) is a popular model for the understanding of human learning and problem-solving skill and to predict human behavior and performance. Since the 1950s [21], thousands of researchers have used IRT in fields, e.g., education, medicine, and psychology, and this includes many critical contexts such as survey analysis, popular questionnaires, medical diagnosis, and school system assessment.
More recently, computer-assisted open-access learning has gotten more popular worldwide, e.g., Khan Academy, Coursera, and EdX have developed a new challenge to handle large-scale student and trace performance [15].
In the deep learning domain, a revolution in deep generative models via variational autoencoders [12] [14], has demonstrated an impressive ability to perform fast inference for complex MIRT models. In this research, we present a novel application of variational autoencoders to MIRT, explore independent and correlated latent traits in the MIRT model via simulated data, and apply them to real-world examples. We then show the impact of Q-miss (wrong Q-matrix) when mixed compared with the original Q-matrix (Q-true).
Specifically, in this paper, we have explored two research questions as follows: first, how to use variational autoencoder in the estimation of MIRT models with large numbers of correlated and independent latent traits? Second, how are the effects of various factors such as the percentage of misfit items in the test and item quality (e.g., discrimination) on item and model fit in case of misspecification of Q-matrix?
Most closely related to the present work, Converse [2] utilized variational autoencoders(VAE) to estimate item parameters with correlated latent abilities and directly compared ML2P-VAE with traditional methods. Curi [1] introduces novel variational autoencoders to estimate item parameters with independent latent traits. Guo [16] explored the neural network approach and compared the outcome with the DINA model. Converse [3] compared outcomes between autoencoders (AE) and variational autoencoders (VAE). Wu [21] investigated the novel application of variational inference and incorporated IRT in the model via simulated and real data. Different from Converse [2], and Curri [1], we use both independent and latent traits in the VAE model. Moreover, we have explored the effect of Q-matrix misspecification in MIRT parameter estimation via different fit statistics, e.g., RMSE, BIAS, AIC, BIC score measures.
The Multidimensional Logistic 2-Parameter (ML2P) model gives the probability of students answering a particular question as a continuous function of student ability [14]. There are two types of parameters associated with each item: a difficulty parameter for the item , and a discrimination parameter for each latent trait, quantifying the hierarchy of ability required to answer the item correctly. The ML2P model gives the probability of a student with latent abilities answering an item correctly as
(1)
2. VARIATIONAL AUTOENCODERS
The variational autoencoder (VAE) is a directed model that uses learned approximate inference and can be trained purely with gradient-based methods[12]. It is similar to auto-encoders but with a probabilistic twist. VAE makes the additional assumption that the low-dimensional representation of data follows some probability distribution , and fits the encoded data to this distribution.
The main use of a VAE as a generative model, VAE generates to after training and feed-forward through the decoder. By Bayes’ rule, we can write the unknown posterior distribution. In our case, we generalized VAE as . In order to keep both P and Q distribution similar, Kullback-Liebler divergence plays a key role in the neural network loss function. The KL-Divergence is given by as follows:
(2)As shown by Kingma and Welling [12] that minimizing Eq. 2 while still reconstructing input data is equivalent to maximizing.
(3)Next, the VAE is trained by a gradient descent algorithm to minimize the loss function. In this case, is the cross-entropy loss function and is a regularization hyperparameter.
(4)Root mean squared error (RMSE): RMSE criterion reflects the average magnitude of the bias between the true item parameters and their associated estimates. A smaller RMSE suggests higher estimation accuracy. Moreover, we also looked into Akaike information criterion (AIC), and Bayesian information criterion (BIC) score to explore MIRT model estimation when using Q-Miss.
First, we have incorporated the independent and correlated latent traits via the ML2P-VAE model proposed by Curi [1], and Converse [2]. We have extended this work by validating Q-matrix based on root, mean, square, error (RMSE), BIAS, and Correlation score.
We made modifications to the architecture of the neural network to allow for the interpretation of weights and biases in the decoder as item parameter estimates, and activation values in the encoded hidden layer as ability parameter estimates. As we know, sometimes researchers call neural networks are usually uninterpretable and function as a black-box model. However, following the addition of Q-matrix in the second from the last layer will make NN more interpretable.
The required modifications are as follows. The decoder of the variational autoencoder has no hidden layers. The non-zero weights in the decoder, connecting the encoded distribution to the output layer, are determined by a given Q-matrix [19]. Thus, these two layers are not densely connected. The output layer must use the sigmoid activation function as follows:
(5)When latent traits are assumed to be correlated, a full correlation matrix must be provided for the ML2P-VAE model. However, a correlation matrix is not required when latent traits are assumed to be independent. This corresponds to the fixed covariance matrix . ML2P-VAE can estimate ability, discrimination, and difficulty parameters, but it does not estimate correlations between latent traits.
Also, the input to our neural network consists of nodes, representing items on an assessment. After a sufficient number of hidden layers of sufficient size, the encoder outputs K + K(K + 1)/2 nodes. The architecture for correlated latent traits is more complex than we think (See Visualization of Deep-VAE architecture for two correlated latent traits and ten input items model via this link[tinyurl.com/aied22].
2.1 Q-Matrix and Misspecification of Q-matrix
Specification of Q-matrix is mainly criticized because of its subjective nature [17]. Misspecification in the cognitive diagnostic model (CDM) mostly occurs because of the types of the attributes, construct of the attribute, Q-matrix, or selected cognitive diagnostic model [6]. In this experiment, we utilized only a misfit source because Q-matrix misspecification was examined, and no changes were made in students’ responses. In the study, the Q-matrix was misspecified by a mixed approach, and misfit items used in this study are presented in Table 1 (See misfit items table in Appendix 2:tinyurl.com/aied22). When the Q-matrix was misspecified, one attribute was translated from 1 to 0, and another attribute was translated from 0 to 1, but the number of measured attributes didn’t change, which is referred to as mixed.
In the architecture of the model ML2P-VAE, we train the neural network with the ADAM optimizer (pure stochastic gradient descent). A simulated assessment with six latent abilities used two hidden layers of sizes 50 and 25. The largest network we used was for an assessment of 20 latent abilities, which utilized two hidden layers of sizes 100 and 50.
3. THE DEEP-Q ALGORITHM
For convenience, we are calling this algorithm the Deep-Q algorithm. The steps of the Deep-Q algorithm are as follows-
Step 1: Use the variational autoencoder and multidimensional item response theory (Ml2P-VAE) model [2] to estimate students’ ability and item parameters based on Q-True and the response data. Step 2: Compute all items’ via RMSE, BIAS, and Correlation test score values based on Q-True and the student’s ability and item parameters estimated at Step 1. We also use AIC and BIC scores to compare Q-true and Q-miss. Step 3: Randomly misspecify Q-true by 10% and 20% to change Q-True. Step 4: Repeat step-1 with Q-miss (Q-miss, Step 3). Step 5: Compare Q-True(top row, boldface) with Q-miss. Q-true should yield a small RMSE/BIAS and a strong correlation score, AIC, and BIC score for difficulty, discrimination, and ability parameters.
4. METHODOLOGY
We ran experiments on two data sets: (i) 6 traits, 35 items, and 18000 students, and (ii) 20 traits, 200 items, and 60,000 students. It is also important to mention here that true parameter values, for both students and items, are only available for simulated data. When simulating data, we used the Pythons SciPy package to generate a symmetric positive definite matrix with 1s on the diagonal (correlation matrix) and all matrix entries non-negative. All latent traits had correlation values between 0,1. We assumed that each latent trait was mean-centered at 0. Then, we sampled ability vectors to create simulated students. We generated a random Q-matrix where each entry . If a column for each element after sampling from this Bernoulli distribution, one random element was changed to a 1. Discrimination parameters were sampled from a range so from 0.25 to 1.75 for each item i, and difficulty parameters were sampled uniformly from - 3 to 3. Finally, response sets for each student were sampled from the ML2P model using these parameters.
5. RESULTS
All experiments were conducted using TensorFlow for R and the ML2Pvae package [4] on an iMac computer with a 3.1 GHz Intel Core i5 via Google Colab Premium, 12 GB NVIDIA Tesla K80 GPU.
Table 1 presents the estimation accuracy of Q under Q-True and Q-miss. The range of values for each criterion is provided in the second and third row of Table 1, and the numbers in bold denote better performance in the associated criterion for the corresponding method, e.g., Q-Miss.
| Data Set | Misspecification | Method | a.RMSE | a.BIAS | a.Corr | b.RMSE | b.BIAS | b.Corr | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Q_True | 0.1465 | 0.0100 | 0.9427 | 0.0750 | 0.0100 | 0.9988 | 0.8120 | 0.0476 | 0.5815 | ||
N=18000 | 10%_Miss | Q_Miss | 0.2297 | 0.0195 | 0.8562 | 0.0993 | 0.0083 | 0.9986 | 0.8398 | 0.0637 | 0.5486 |
| 20%_Miss | Q_Miss | 0.2621 | 0.0466 | 0.7984 | 0.1684 | 0.0268 | 0.9962 | 0.8684 | 0.1660 | 0.5351 | |
| Q_True | 0.1007 | 0.0259 | 0.9094 | 0.2098 | -0.0186 | 0.9984 | 0.5614 | -0.0013 | 0.8686 | ||
N=60000 | 10%_Miss | Q_Miss | 0.2525 | 0.0654 | 0.8430 | 0.2881 | 0.0129 | 0.9926 | 0.7288 | 0.0037 | 0.6859 |
| 20%_Miss | Q_Miss | 0.2200 | 0.0367 | 0.8777 | 0.2191 | 0.0243 | 0.9952 | 0.6561 | 0.0166 | 0.7551 |
Overall, Table-1 indicates that the Deep-Q method yields a better fit statistic score and strong correlation score than the Q-miss situation when using a wrong Q-matrices. This result is corroborated by the correlation plots between the true discrimination parameters and the weights of the decoder, displayed in Fig. 1 and 2 (follow this url: tinyurl.com /aied22 for larger view of plots)
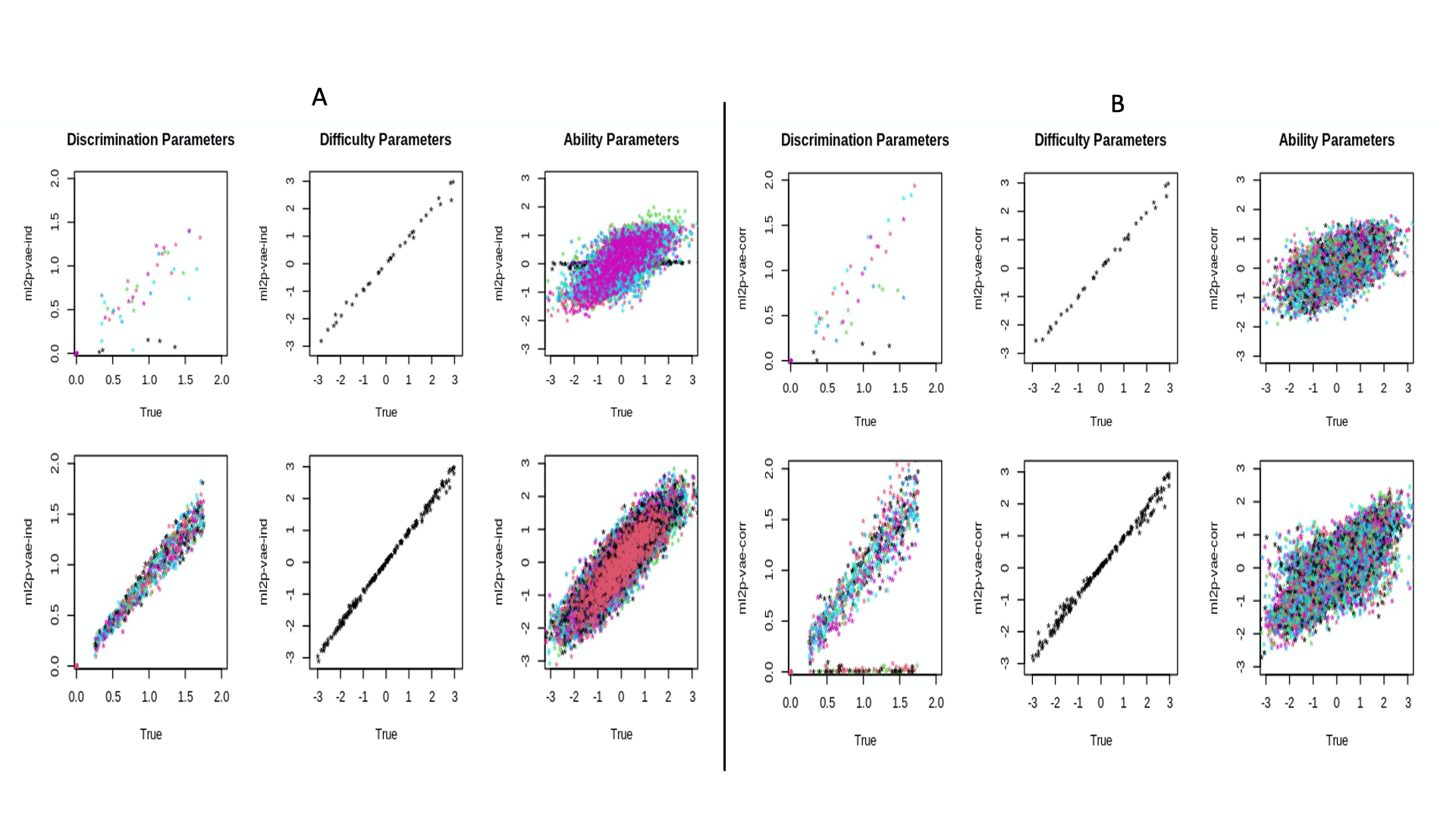
In addition, Q-matrix validation measures via AIC, BIC score for discrimination (a), difficulty (b), and ability parameters with correlated latent traits remain consistent with Table-1 outcome (see AIC, BIC score:Appendix 5:[tinyurl.com /aied22])
In Fig 1(A and B), the correlation plots of discrimination parameter estimate for data with items and latent traits. Each color represents discrimination parameters relating to one of each latent skill. In the ability parameter, each color in the plot represents discrimination and ability parameters associated with each latent trait. Difficulty parameters are on the item level, not the latent trait level. So in each item, I have exactly one difficulty parameter , regardless of the number of latent skills. The interpretation is similar for independent latent traits, as described in figure 1(A). Plots show correlated latent traits and show better outcomes compared to independent latent traits.
6. DISCUSSION AND CONCLUSION
An incorrect Q-matrix can lead to a significant change in the assessment outcomes when applied to CDMs. As a result, a Q-matrix validation strategy to reduce assessment error is becoming increasingly important. Several approaches, including EM-based and non-parametric methods, have shown the ability to identify and create an acceptable Q-matrix. However, to the best of the authors’ knowledge, their experiment utilizes traditional IRT parameter estimation where they utilize low-dimensional latent traits and students’ responses. However, the Deep-Q algorithm is most useful with high and low-dimensional data.
Moreover, Converse’s [2] study shows that MIRT parameter estimation results via the Ml2P-VAE model are competitive compared to traditional IRT parameter estimation methods. Our study used a Deep-Q algorithm, a deep learning-based algorithm, to identify and validate a Q-matrix for small and large-scale latent traits. Deep-Q could be useful for large-scale assessments, e.g., PISA and TIMSS.
ML2P-VAE is a novel technique that allows IRT parameter estimation of independent and correlated low and high-dimensional latent traits. Ultimately, it can be said that the Deep-Q algorithm succeeds in detecting misfit items in both large and small sample cases. ML2P-VAE methods and Deep-Q are most useful on high-dimensional data, but even when applied to smaller data sets where traditional techniques are feasible, the results from current methods are competitive.
7. ACKNOWLEDGMENTS
This research was sponsored by the National Science Foundation under the award The Learner Data Institute (bit.ly/36Bi93m) (award 1934745). The opinions, findings, and results are solely the authors’ and do not reflect those of the funding agencies. Thanks to Geoff Converse, Andrew Ott, and LDI team for their suggestions and comments.
8. REFERENCES
- Curi, M., Converse, G. A., Hajewski, J., Oliveira, S.: Interpretable variational autoencoders for cognitive models. 2019 International Joint Conference on Neural Networks (IJCNN) 1-8. IEEE.(2019).DOI: 10.1109/IJCNN.2019.8852333
- Converse, G., Curi, M., Oliveira, S., Templin, J.: Estimation of multidimensional item response theory models with correlated latent variables using variational autoencoders. Machine Learning, 1-18.(2021). DOI:10.1007/s10994-021-06005-7
- Converse, G., Curi, M., Oliveira, S.: Autoencoders for educational assessment. International Conference on Artificial Intelligence in Education.41-45.Springer.(2019).https://doi.org/10.1007/978-3-030-23207-8-8
- Converse, G.: ML2Pvae: VAE models for IRT parameter estimation.(2020) https://CRAN.R-project.org/package=ML2Pvae, r package version1.0.0.
- Liu, C. W., Chalmers, R. P.: Fitting item response unfolding models to likert scale data using mirt in R. PloS one. 13(5).(2018). https://doi.org/10.1371/journal.pone.0196292
- Chen, J., de la Torre, J., Zhang, Z.: Relative and absolute fit evaluation in cognitive diagnosis modeling. Journal of Educational Measurement, 50(2),123-140.(2013).https://doi.org/10.1111/j.1745-3984.2012.00185.
- Kingma, D. P., Welling., M.: Auto-encoding variational bayes. (2013). https://doi.org/10.48550/arXiv.1312.6114
- Rezende, D. J., Mohamed, S. and Wierstra, D.: Stochastic backpropagation and approximate inference in deep generative models. (2014).https://doi.org/10.48550/arXiv.1401.4082
- Harris, D.: Comparison of 1-, 2-, and 3-parameter IRT models. Educational Measurement: Issues and Practice,8(1), 35-41. (1989).https://doi.org/10.1111/j.1745-3992.1989.tb00313.x
- Leighton, J. P., Gierl, M. J., Hunka,S. M.: The attribute hierarchy method for cognitive assessment: A variation on Tatsuoka’s rule-space approach. J. Educ. Meas., vol. 41, 205–237,(2004). https://doi.org/10.1111/j.1745-3984.2004.tb01163.x
- Torre, J. de la. and Chiu,C. Y.,:A General Method of Empirical Q-matrix Validation,” Psychometrika, vol. 81, no. 2, 253–273.(2016). DOI: 10.1007/s11336-015-9467-8
- Kingma, D. P., Welling, M.: Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114.(2013). https://doi.org/10.48550/arXiv.1312.6114
- DeCarlo, L. T.: On the analysis of fraction subtraction data: The DINA model, classification, latent class sizes, and the q-matrix. Appl. Psychol. Meas., vol. 35, no. 1,8–26 ,(2011).https://doi.org/10.1177/0146621610377081
- McKinley, R., Reckase, M.: The use of the general Rasch model with multidimensional item response data. American College Testing. (1980)
- Piech C., Bassen J., Huang J., Ganguli S., Sahami M., Guibas LJ., Sohl-Dickstein J.: Deep knowledge tracing. Advances in neural information processing systems. 28.(2015)
- Guo, Q. Cutumisu, M., Cui, Y.: A neural network approach to estimate student skill mastery in cognitive diagnostic assessments. (2017).https://doi.org/10.7939/R35H7C71D
- Rupp, A. A., Templin, J.: The effects of Q-matrix misspecification on parameter estimates and classification accuracy in the DINA model. Educational and Psychological Measurement, 68(1), 78-96.(2008).https://doi.org/10.1177/0013164407301545
- Rezende, D. J., Mohamed, S., Wierstra, D.: Stochastic backpropagation and approximate inference in deep generative models. In International conference on machine learning 1278-1286. PMLR. (2014).https://doi.org/10.48550/arXiv.1401.4082
- Tatsuoka, K.K.: Rule space: an approach for dealing with misconceptions based on item response theory. J. Educ. Meas. 20(4), 345–354 (1983)
- Ma, W., Torre,J. de la.: An empirical Q-matrix validation method for the sequential generalized DINA model. Br. J. Math. Stat. Psychol., (2019). https://doi.org/10.1111/bmsp.12156
- Wu, M., Davis, R. L., Domingue, B. W., Piech, C., Goodman, N.: Variational item response theory: Fast, accurate, and expressive. arXiv preprint arXiv:2002.00276.(2020).https://doi.org/10.48550/arXiv.2002.00276
- Zhang, J., Shi, X., King, I., Yeung, D. Y.: Dynamic key-value memory networks for knowledge tracing. In: 26th International world wide web conference (WWW 2017) 765–774.(2017). https://doi.org/10.1145/3038912.3052580
Please follow this link for additional references (Appendix 6): tinyurl.com/aied22
9. APPENDIX
Please follow this link for Appendixes: tinyurl.com/aied22
© 2022 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.