ABSTRACT

To improve student learning outcomes within online learning platforms, struggling students are often provided with on-demand supplemental instructional content. Recently, services like Yup (yup.com) and UPcheive (upchieve.org) have begun to offer on-demand live tutoring sessions with qualified educators, but the availability of tutors and the cost associated with hiring them prevents many students from having access to live support. To help struggling students and offset the inequities intrinsic to high-cost services, we are attempting to develop a process that uses large language representation models to algorithmically identify relevant support messages from these chat logs, and distribute them to all students struggling with the same content. In an empirical evaluation of our methodology we were able to identify messages from tutors to students struggling with middle school mathematics problems that qualified as explanations of the content. However, when we distributed these explanations to students outside of the tutoring sessions, they had an overall negative effect on the students’ learning. Moving forward, we want to be able to identify messages that will promote equity and have a positive impact on students.

Keywords

1. INTRODUCTION

Middle school mathematics students have been shown to benefit from on-demand support when struggling within online learning platforms [8]. These supports require time and expertise to create, which can impede the platform’s ability to provide support at scale. Additionally, when attempting to personalize students’ online educational experience, it is essential to have multiple supports available for the same content. There has been notable success when crowdsourcing these supports from the teachers that use the platform [5, 6], but there are other opportunities to collect supports, including from live chat logs between students and tutors, which are an intuitive resource for generating support messages because they contain messages from a tutor explaining how to solve a problem to a student. Therefore, we propose the utilization of large language representation models to algorithmically identify support messages from live tutors that can be distributed to students at scale. At this point, we have created and evaluated a method for identifying relevant tutor messages from chat logs. However, while our method was able to identify messages that seemed equivalent to explanations already used in ASSISTments, the results of an empirical evaluation of these messages’ ability to help students found that they negatively impacted learning. We are looking for critiques of our existing method and ways in which we can expand our method to account for more than just the semantic similarity between tutor messages and existing explanations in order to improve student learning outcomes.

2. METHODOLOGY

2.1 Data Collection

The student-tutor chat log data comes from the ASSISTments online learning platform [4] and UPchieve [2]. From June 9th, 2021 to November 5th, 2021, 82 students from 5 different classes had the opportunity to request help from a live UPchieve tutor within the ASSISTments learning platform. Over this time, students requested help 208 times and 8,817 messages were exchanged between students and tutors. In this work, we attempted to extract generalizable support from the live tutors’ messages. Our approach relies on comparing large language model embeddings of the messages written by live tutors to the explanations already used as on-demand support within ASSISTments. Therefore, we also collected 16,130 existing explanations from the ASSISTments platform.

2.2 Identifying Generalizable Support

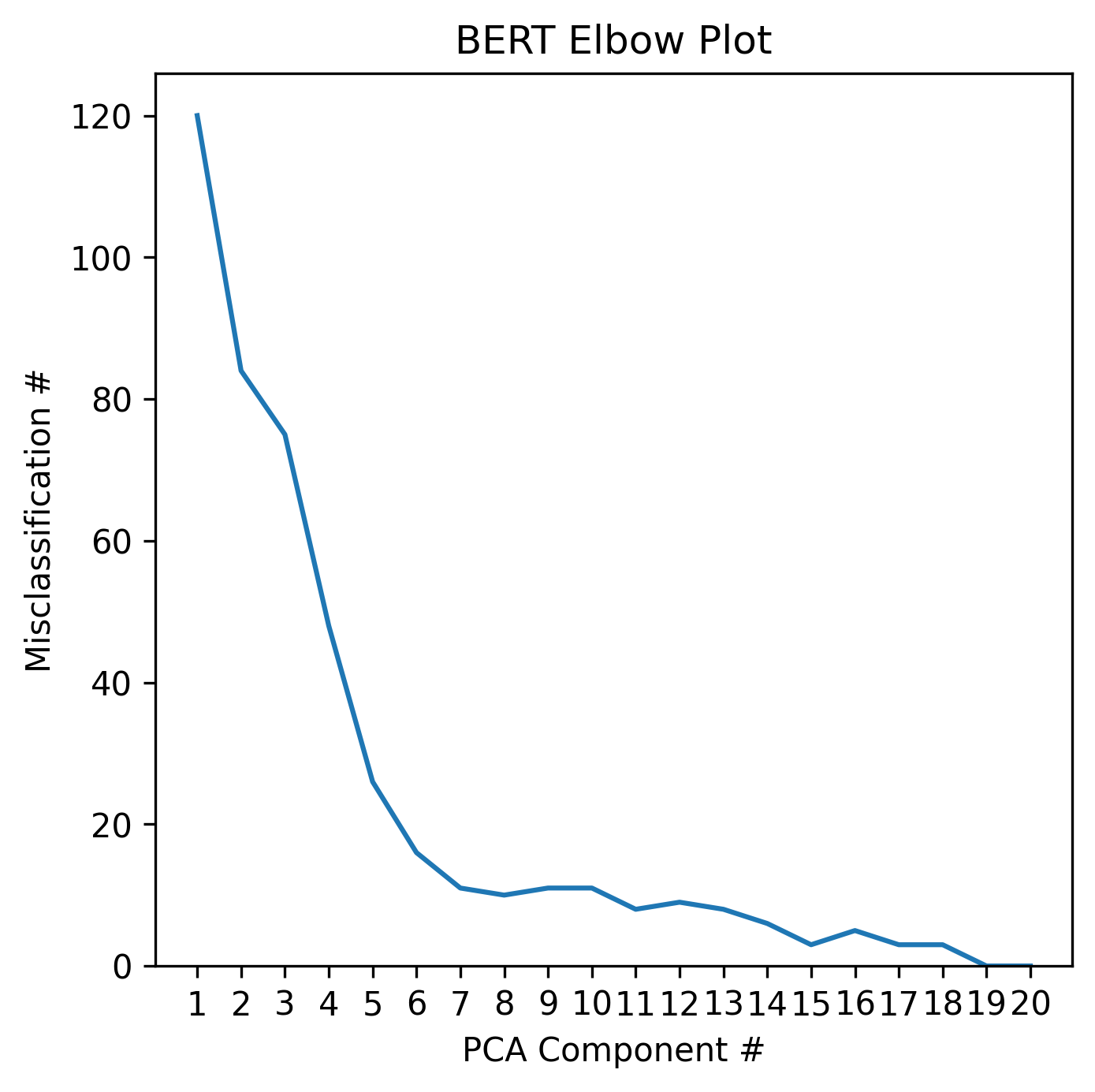
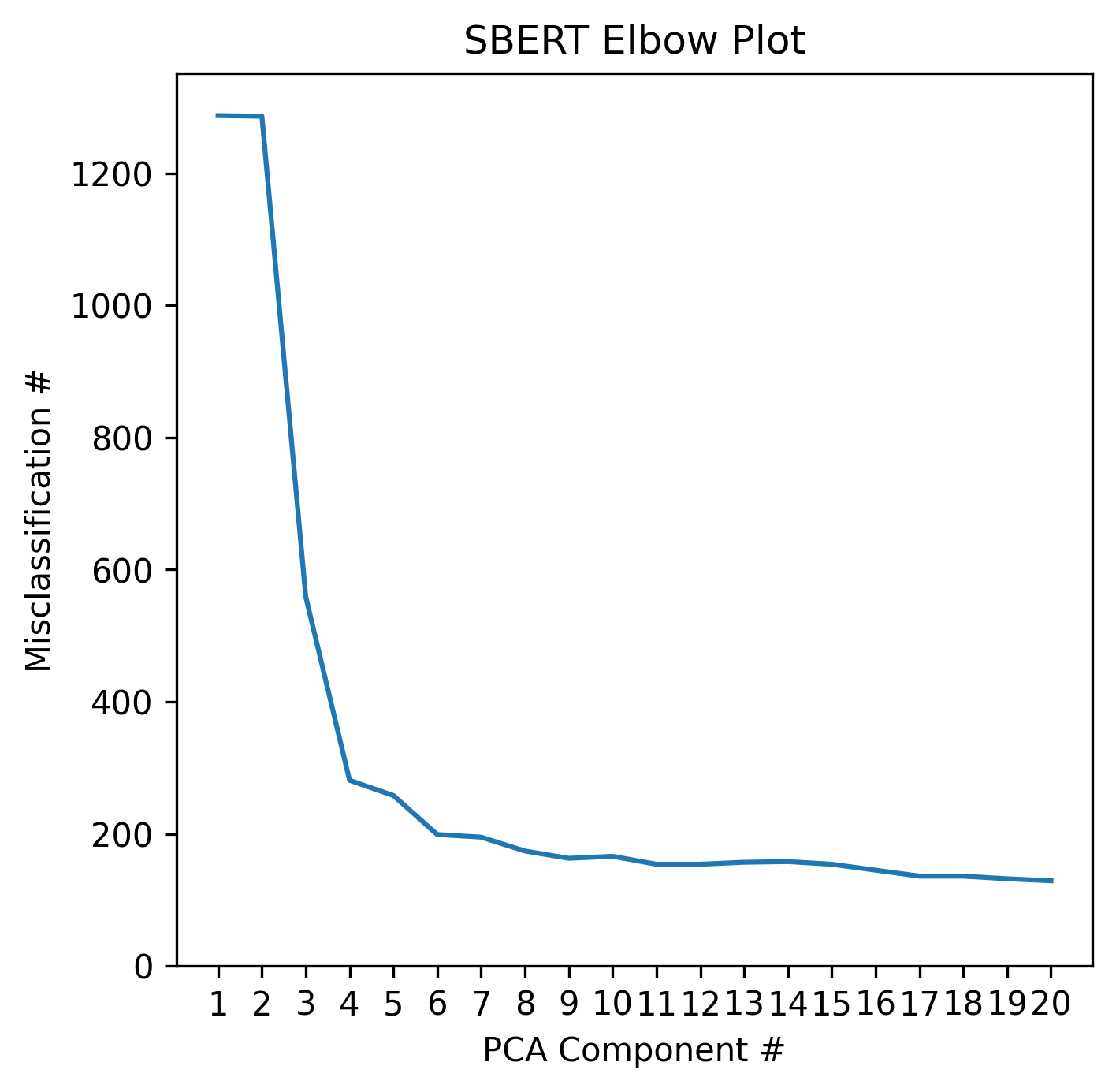
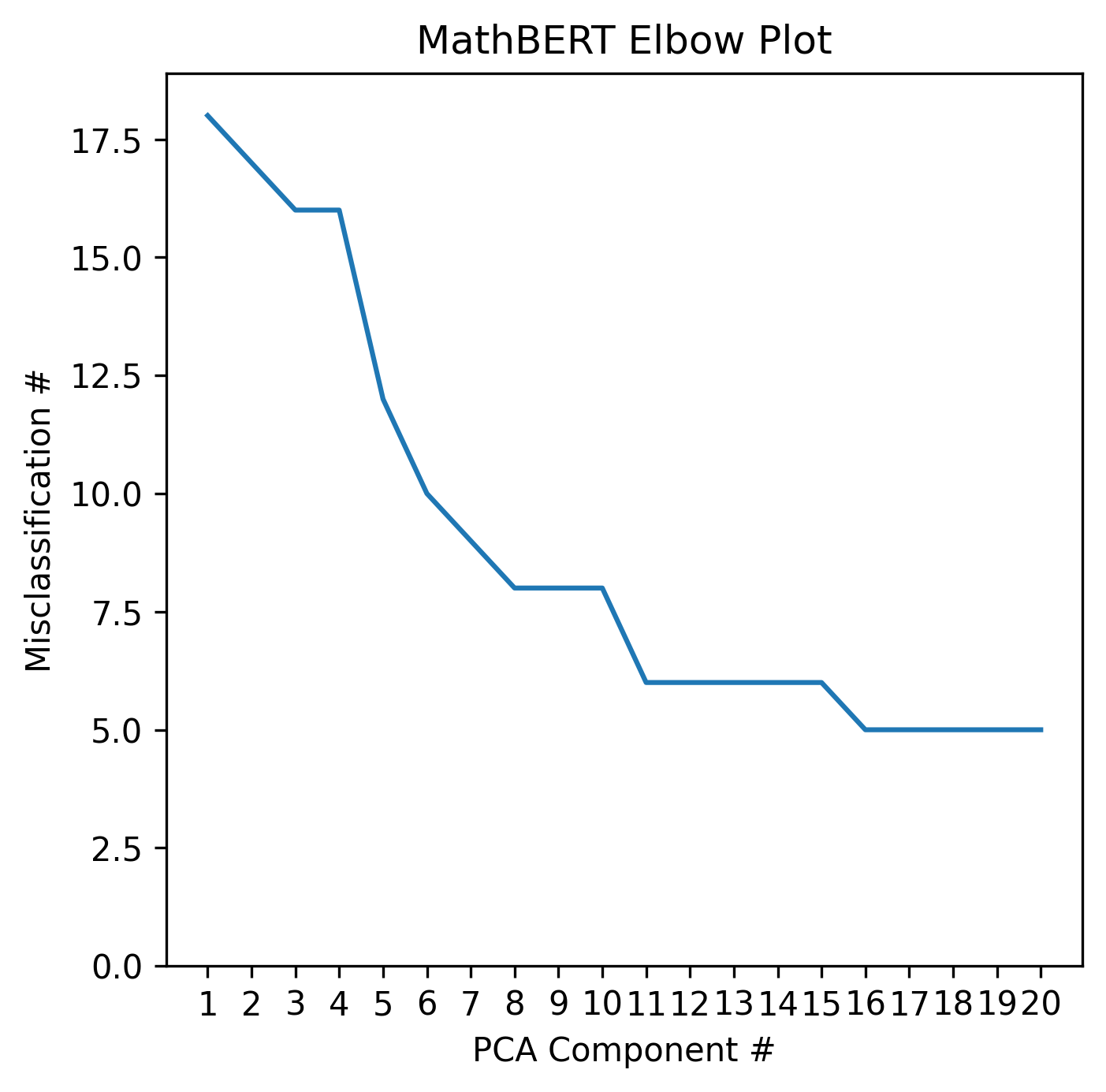
To identify generalizable support, we employ a four-step approach. The first step of our approach is to embed each tutor message and ASSISTments explanation using a large language representation model. We experimented with embeddings using three different pretrained large language models: BERT [3], SBERT [7], and MathBERT [9]. Due to the large number of features in these embeddings, the second step of our approach was to transform the embeddings using PCA [1] to mitigate over-fitting our subsequent supervised model. The third step was to train a logistic regression to classify whether the embedded sample represented a tutor message or an ASSISTments explanation. The fourth step was to manually inspect the misclassified tutor messages and evaluate their generalizability and relevance. If they were deemed relevant, than they were included in the empirical study within ASSISTments. To select the number of PCA components to use for each logistic regression, a separate logistic regression was fit on $1$ through $n$ components, in order of decreasing significance, where $n$ is the total number of components. After each logistic regression was fit, the total number of tutor messages classified as ASSISTments explanations was calculated and plotted. The plot revealed an "elbow", at which point additional PCA components had diminished effects on the accuracy of the logistic regression. Therefore, the number of components at the elbow of the graph was selected as the correct number of components to mitigate over-fitting.

2.3 Empirical Study

After candidate tutor messages were identified using the process described in Section 2.2, a randomized controlled experiment was performed within ASSISTments, in which an assignment consisting of six mathematics problems was given to middle school students. Only teachers that felt the problems were appropriate for their class allowed their students to participate in the experiment. For the 1st, 3rd, and 5th problems, students were randomized between receiving the identified tutor messages, or just the answer, as support upon their request. For the 2nd, 4th, and 6th problems, students were given a nearly identical problem with the same format and knowledge prerequisites as the previous problem. Within the assignment, the order that the students received the three pairs of problems was also randomized to eliminate bias from completing the problems in a particular order. The students’ success on the 2nd, 4th, and 6th problems was used to evaluate the quality of the tutoring for each of the previous problems respectively. To determine the effectiveness of the tutor messages, an intent to treat analysis was performed in which Welch’s $t$-tests [10] were used to compare the next-problem correctness of students that could have received the tutor messages and students that could have received the answer when requesting support, and Cohen’s $d$ was used to determine the effect size of the treatment compared to the control.

3. RESULTS

3.1 Identifying Generalizable Supports

Applying the elbow sample selection method described in Section 2.2 for each of the three different BERT models resulted in the plots shown in Figure 1. Only the first 20 PCA components are plotted because the elbow is always in the first 20 components. Based on Figure 1, MathBERT was the most accurate model and only misclassified eight tutor messages as explanations at the elbow, which is about 0.16% of all the tutor messages. To further illustrate the difference in the effectiveness of each BERT model, Figure 2 shows a two-dimensional projection of the regression boundary when fit using $n$ PCA components, where $n$ is determined by the elbow plots in Figure 1. Again, MathBERT has the least misclassifications. For this reason, the misclassified tutor messages from the logistic regression fit using the first eight PCA components of the MathBERT embedding were used as candidate tutor messages for the empirical study. Of the eight messages, six were relevant enough to be used as on-demand support for the problems for which they were written. The other two messages were written about an example problem devised by the tutor, and not the original problem the student was trying to solve.

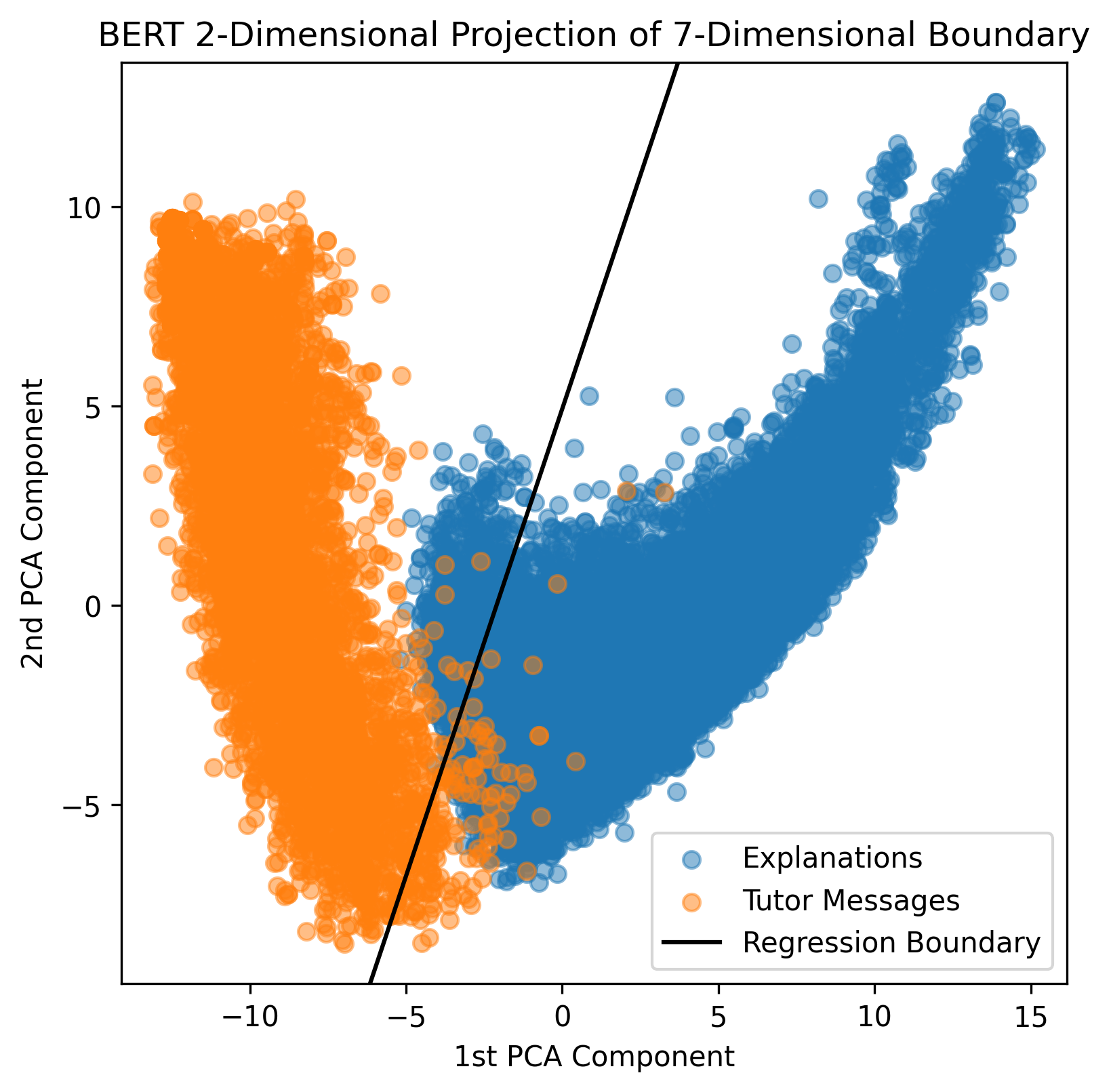
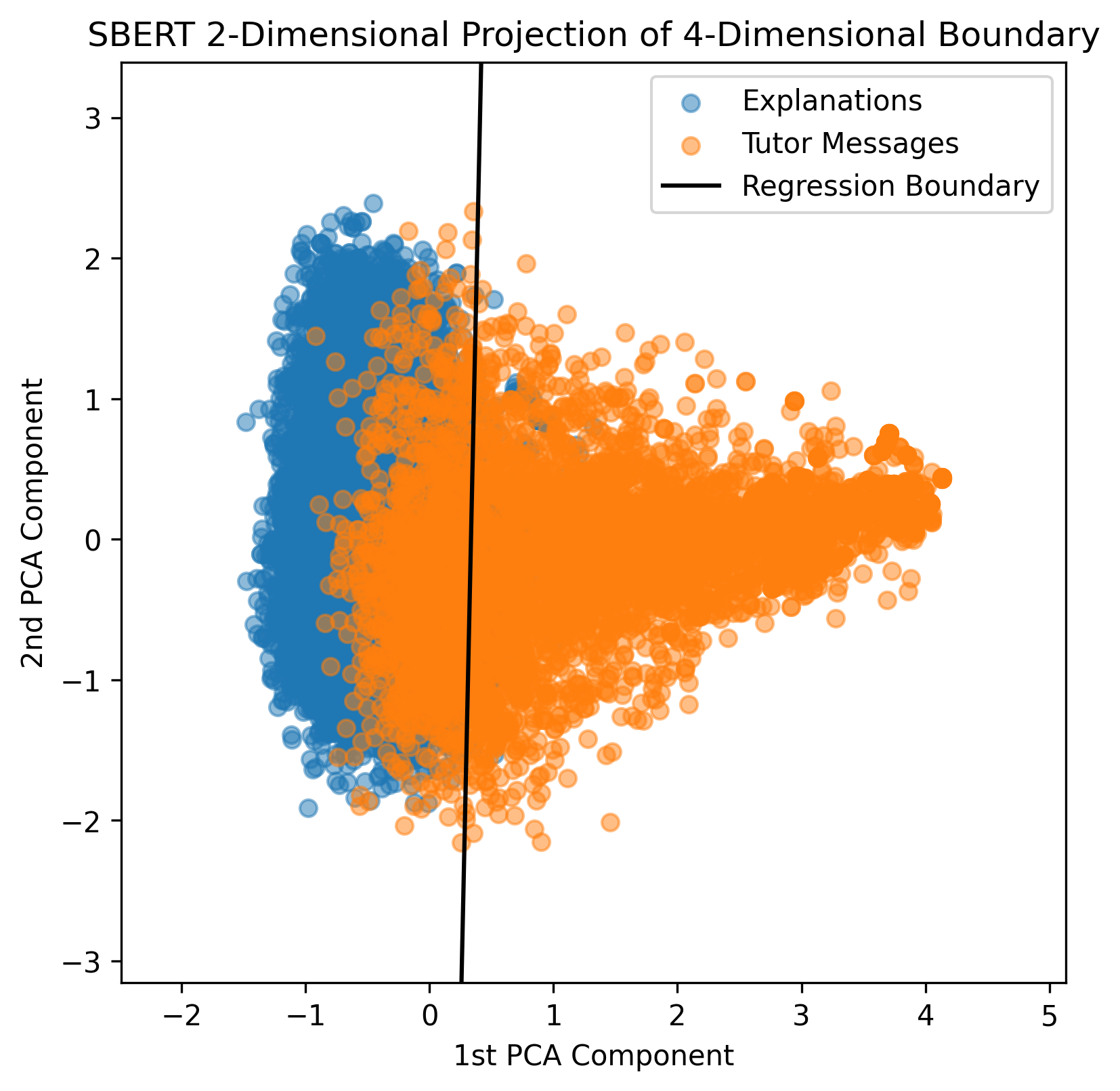
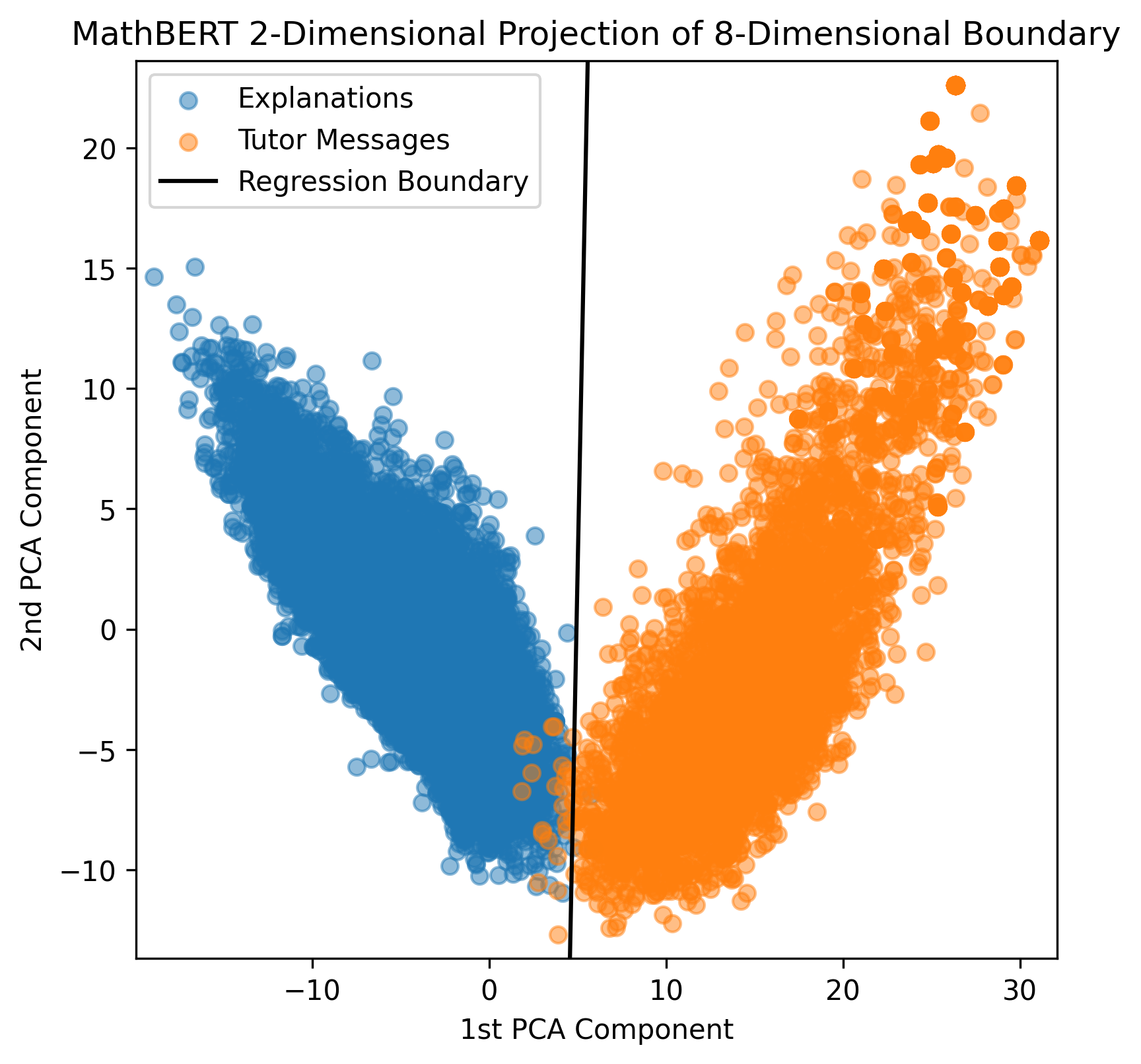
3.2 Empirical Study

The six selected tutor messages were written during discussion with students requesting support on three problems in ASSISTments. Therefore, the messages for each problem were combined into one set of on-demand support for the problem. Figure 3 shows each of the problems and the on-demand support created for them. In total, 163 students participated in the experiment. 106, 97, and 111 students were used to evaluate the supports for Problems 1, 2, and 3 respectively. Overall, there was a small, statistically insignificant negative effect from offering students tutor messages for support ($d$ = -0.145, $p$ = 0.068). When evaluating the effectiveness of the tutor message based supports for each individual problem, it was revealed that for the first and third problem, there was an insignificant negative effect from receiving on demand tutoring ($d$ = -0.094 and -0.069 respectively, $p$ = 0.489 and 0.627 respectively), but for the second problem, there was a medium-sized significant negative effect ($d$ = 0.406, $p$ = 0.005).

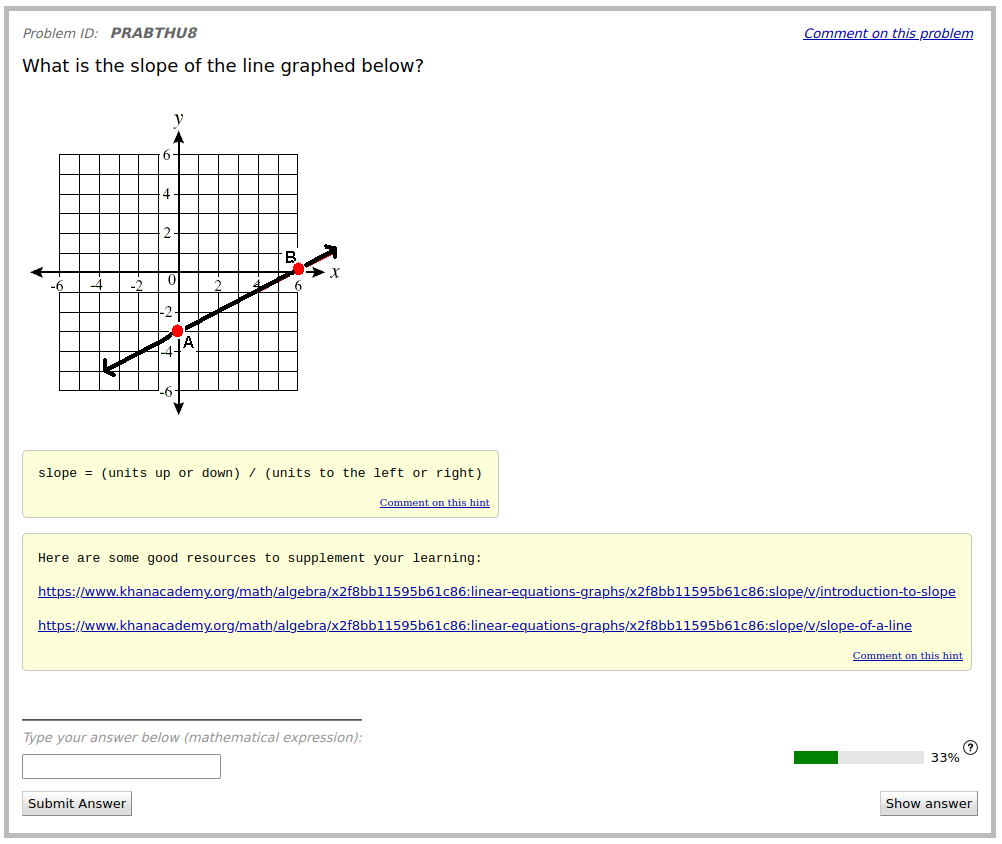
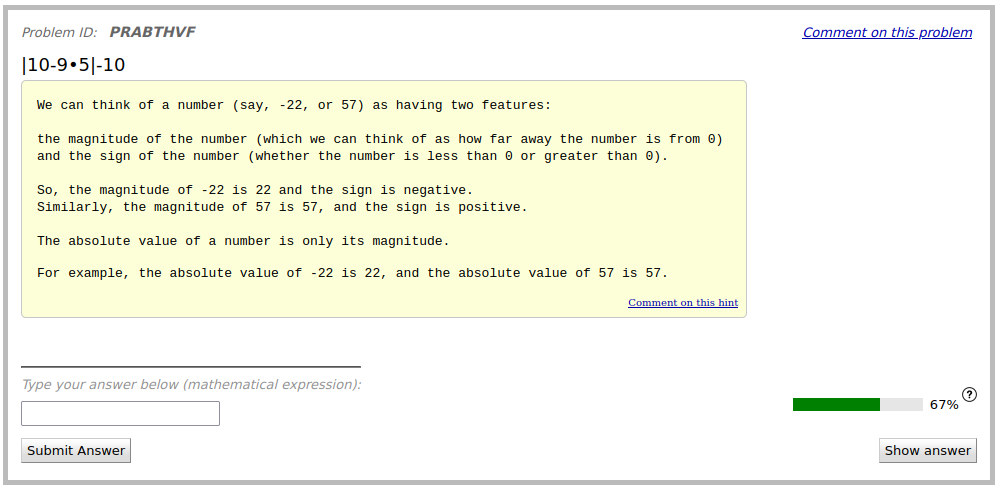
4. CONCLUSION

Although we were able to identify tutor messages that offered explanations to students on how to solve the problem they were struggling with, only 75% of the messages selected by our methodology were deemed relevant by human selection, and in an empirical study, these messages had a negative effect on real students’ learning. This implies that there is more nuance to how helpful a message will be aside from how similar it is semantically to existing support messages. While this seems obvious, it is difficult to approach algorithmically filtering the tutor messages in a way that takes into account their relevance to the problem and how likely they are to benefit student learning outcomes. Moving forward, research efforts may compare tutor messages to the relevant problem, either in an embedding space or simply through phrase matching. This could help exclude tutor messages which were not relevant to the original problem but did get misclassified as supports in the embedding space. To address the negative impact that the selected tutor messages had on students’ learning, we could attempt to use the students’ responses in the student-tutor chat logs to identify only the tutor messages followed by student messages with positive sentiment, for example, "Thank you! I understand now". Ideally, by filtering the tutor messages this way, we would only include tutor messages that the student was happy to receive, which implies these messages would be more likely to help other students. Additionally, a metric to quantify the benefit to student learning outcomes given a problem and support would benefit our analyses of relevant tutoring logs. There are many factors to consider when improving student learning outcomes and we look forward to investigating these potential directions.

5. ACKNOWLEDGMENTS

We would like to thank NSF (e.g., 2118725, 2118904, 1950683, 1917808, 1931523, 1940236, 1917713, 1903304, 1822830, 1759229, 1724889, 1636782, 1535428), IES (e.g., R305N210049, R305D210031, R305A170137, R305A170243, R305A180401, R305A120125), GAANN (e.g., P200A180088 P200A150306), EIR (U411B190024), ONR (N00014-18-1-2768) and Schmidt Futures.

6. REFERENCES

1. H. Abdi and L. J. Williams. Principal component analysis. Wiley interdisciplinary reviews: computational statistics, 2(4):433–459, 2010.
2. J. Bryant, L.-K. Chen, E. Dorn, and S. Hall. School-system priorities in the age of coronavirus. McKinsey & Company: Washington, DC, USA, 2020.
3. J. Devlin, M.-W. Chang, K. Lee, and K. Toutanova. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805, 2018.
4. N. T. Heffernan and C. L. Heffernan. The assistments ecosystem: Building a platform that brings scientists and teachers together for minimally invasive research on human learning and teaching. International Journal of Artificial Intelligence in Education, 24(4):470–497, 2014.
5. T. Patikorn and N. T. Heffernan. Effectiveness of crowd-sourcing on-demand assistance from teachers in online learning platforms. In Proceedings of the Seventh ACM Conference on Learning@ Scale, pages 115–124, 2020.
6. E. Prihar, T. Patikorn, A. Botelho, A. Sales, and N. Heffernan. Toward personalizing students’ education with crowdsourced tutoring. In Proceedings of the Eighth ACM Conference on Learning@ Scale, pages 37–45, 2021.
7. N. Reimers and I. Gurevych. Sentence-bert: Sentence embeddings using siamese bert-networks. arXiv preprint arXiv:1908.10084, 2019.
8. J. Roschelle, M. Feng, R. F. Murphy, and C. A. Mason. Online mathematics homework increases student achievement. AERA open, 2(4):2332858416673968, 2016.
9. J. T. Shen, M. Yamashita, E. Prihar, N. Heffernan, X. Wu, B. Graff, and D. Lee. Mathbert: A pre-trained language model for general nlp tasks in mathematics education. arXiv preprint arXiv:2106.07340, 2021.
10. B. L. Welch. The generalization of ‘student’s’problem when several different population varlances are involved. Biometrika, 34(1-2):28–35, 1947.

© 2022 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.