ABSTRACT
Recent research on more comprehensive models of student learning in adaptive math learning software used an indicator of student reading ability to predict students’ tendencies to engage in behaviors associated with so-called “gaming the system." Using data from Carnegie Learning’s MATHia adaptive learning software, we replicate the finding that students likely to experience reading difficulties are more likely to engage in behaviors associated with gaming the system. Using both observational and experimental data, we consider relationships between student reading ability, readability of specific math lessons, and behavior associated with gaming. We identify several readability characteristics of specific content that predict detected gaming behavior, as well as evidence that a prior experiment that targeted enhanced content readability decreased behavior associated with gaming, but only for students that are predicted to be less likely to experience reading difficulties. We suggest avenues for future research to better understand and model behavior of math learners, especially those who may be experiencing reading difficulties while they learn math.
Keywords
1. INTRODUCTION
Over two decades of research on intelligent tutoring systems (ITSs) and adaptive learning software has explored data-driven modeling of student behavior with so-called “detector” models of patterns of engagement that may indicate, for example, that a student is potentially “gaming the system” (e.g., [5, 7, 8, 9, 13]).
Gaming the system is typically described as behavior associated with a student’s use of learning software and supports provided by software in a way that might indicate an effort to make progress without substantive engagement with learning material (e.g., rapidly guessing or using hints extensively). A substantial body of research explores many facets of this construct, especially in software for math learning. Patterns of engagement associated with gaming have been found in some cases to be, at least, “non-harmful” (e.g., [7]) and even potentially to take on productive or helpful forms, as when students may seek out hints that provide the answer to a problem-step to provide a worked example on which they can reflect [34]. Nevertheless, detected gaming the system has generally been found to be negatively associated with various short- and longer-term learning outcomes (e.g., [5, 13, 29, 15]). Researchers have considered software-specific, content-specific, and related contextual factors and features (e.g., [9, 21]) that may relate to patterns of gaming within specific math content. Other research has considered student-level factors that may predict decisions to engage in such behavior (e.g., [4, 30]).
Recent work calls for more comprehensive models of student math learning that include “non-math” factors like reading comprehension [30, 3]. We focus on the relationship among inferred reading ability, detected gaming the system behavior, and learning outcomes, relying on both student-level factors and characteristics of particular math lessons. Replicating a finding that, overall, students likely to experience reading difficulties are more likely to engage in behaviors associated with “gaming the system” [30], we focus on features that track the readability of math content to consider the extent to which content-level factors related to reading may help to explain this observed correlation.
If behavior associated with gaming is more likely to occur across all content for learners who may experience reading difficulties, then students with reading difficulties may engage in behaviors like rapid help seeking, for example, as a reasonable strategy to try to make progress. However, students may engage in this behavior to a greater extent in content that could present reading-related obstacles compared to less reading-intensive content. If so, content-oriented improvements to readability, for example, might be an appropriate approach to decrease less productive engagement (i.e., gaming behavior) and improve students’ learning experiences.
We use data-driven prediction models of students’ reading ability, a detector model for gaming the system, and several potential measures of math lesson readability over data from several thousand students using adaptive math software. Next, we re-analyze data from a recent experimental study that found decreased time to completion and greater mastery rates for content that had been targeted for readability improvements. We suggest avenues for future research to better understand and model behavior of learners, especially those who may be experiencing reading difficulties while they learn math.
2. BACKGROUND
2.1 Prior Research
Reading comprehension is closely related to math performance [36, 18]. For example, performance on math word problems has been shown to be strongly correlated with performance in reading comprehension [35]. Our work builds on prior research that considers students’ reading ability (or comprehension) during math learning and data-driven detection of behavior often associated with gaming the system while students use adaptive software.
Richey et al. [30] considered the role of reading comprehension within an ITS for math, proposing performance on an introductory lesson (specifically, error and hint request counts, or “assistance”) as a proxy for reading ability. This lesson is designed to introduce students to various features of the software, including a glossary, user-interface elements (e.g., an equation solver), and other supports for learning (e.g., context-sensitive hints). Using this proxy indicator, they found higher instances of behaviors associated with “gaming the system” among readers who, according to their proxy indicator, may be experiencing reading difficulties. More recent work validated this choice of lesson and developed a neural network model that uses student performance within the lesson to predict end-of-year, standardized test scores for English Language Arts (ELA) [3] that can be used to infer student reading ability in real-world contexts. Such contexts, in which student-level reading assessment scores (or similar indicators of reading ability) aren’t available to researchers or learning platform developers, are typical with learning software deployed at scale. We describe this reading ability prediction model in the next section.
Students’ choices to engage in behavior associated with gaming the system could be explained by student-level factors, factors about specific pieces (or subsets of) of content, or both [4, 9]. Baker et al. [9] explore the extent to which features of content in adaptive math software predict students’ frequency of gaming the system. They describe a set of 79 features extracted from the problem content of a set of 22 MATHia (then called Cognitive Tutor) lessons, grouping the features into six factors with principal component analysis. One factor of the six was statistically significant as a predictor of gaming the system frequency, accounting for 29% of the variance in observed gaming the system behavior. They note, “several of the features in this factor appear to correspond to a lack of understandability in the presentation of the content or task..., as well as abstractness... and ambiguity... ” [9]. We suggest that this observation can be further explored by considering readability metrics for math content.
Gaming the system detectors have also been used to better understand mechanisms by which interventions may produce effects on learning outcomes. For example, recent analysis of experimental data found that (decreases in) gaming the system fully mediated positive effects on learning from learners’ use of an educational math game called Decimal Point [31]. We begin to pursue a similar strategy in what follows, considering whether positive effects due to an intervention to improve readability in a math lesson could (partially) be explained by changes in detected gaming the system behavior.
2.2 Learning Context
We consider data from middle school students working in MATHia, an ITS for math learning that is used by hundreds of thousands of learners in the United States every year as a part of their math curriculum [32]. Each grade-level’s content in MATHia consists of approximately 80 to 120 lessons. Many such lessons, and those on which we focus in the present study, provide students with opportunities to learn and demonstrate mastery on a set of granular knowledge components (KCs, or skills) [24] over a set of at least three (but often many more) problems. Each problem has multiple steps, each of which is mapped to one or more KCs. Progress to KC mastery is tracked using Bayesian knowledge tracing [14], with adaptive selection of problems based on the set of KCs that a student has yet to master at any particular time. After a student reaches mastery of all KCs associated with a lesson, they proceed to the next lesson in the prescribed sequence of content (generally for their grade-level). We provide additional details about our data in Section 4.
3. METHODS & MEASURES
3.1 Predicting Student Reading Ability
Following the proposal that features extracted from log data representing student performance in an introductory lesson can serve as a proxy for reading ability [30], a neural network model was developed to predict students’ reading ability [3]. Specifically, the model was trained on student performance data from the introductory activity to predict the probability that they will pass their end-of-year ELA exam scores. The model achieves consistently high accuracy with an AUC as large as 0.8.
The model was validated using a multi-step process, including (a) ensuring the model was not merely predicting math performance (given that ELA and math test scores are highly correlated) by measuring its accuracy on predicting math scores; (b) it was found to generalize to another dataset from a different state and using a different state test; and (c) ensuring that its performance does not vary across broad demographics such as ethnicity and gender [2].
Previous applications of this model call students in the bottom quartile of its predicted probabilities of passing an ELA test “emerging readers” (ER) or “learners likely to experience reading difficulties” while students in the top three quartiles are “non-emerging readers” (non-ER) [1]. We use this model (and student classification based on the model) with data from student work in the introductory lesson in MATHia in both observational and experimental data analyses that follow.
3.2 Gaming the System Detectors
We implement a detector of gaming the system recently developed for MATHia [26]. This model was found to perform well compared to historical models [26] and was also recently evaluated for algorithmic fairness [10]. Training data for models like this are often collected via quantitative field observations that link software log files with observations of trained observers or coded by trained observer-coders using automated replays of log files from the software [6]. The coding process used for the particular model we adopt involves determining whether particular “clips” of learner interactions (either 20 second intervals or up to eight students actions, whichever comes first, extracted using a fixed-stride, non-overlapping approach) with MATHia are instances of behavior judged to be associated with gaming the system. Features that capture various facets of user behavior are then extracted from these log files and used as input to a random forest model that targets prediction of the classification of interaction clips as instances of gaming or not.
3.3 Measures of Math Content Readability
We define math lessons associated with substantial reading (e.g., so-called “word problems”) as having sufficient text to contribute to well-defined quantitative measures of readability from existing literature. Lessons without substantial reading content may focus, for example, on symbolic problem-solving like different forms of equation solving. Using this lesson-level definition, we will compare lessons without substantial reading content to those with substantial reading content to get a baseline understanding of behavior across these two types of lessons.
For the 134 lessons with substantial reading content in our dataset (described in the following section), we consider a set of quantitative readability metrics over problem text in each lesson (i.e., calculated over all of the problems within a lesson and averaged to get a lesson-level metric) to characterize its “readability.” We initially calculated 32 metrics related to readability, including metrics that fall within the following categories:
- basic text structure metrics (e.g., word count, average sentence length)
- vocabulary metrics (e.g., type-token ratio, Shannon entropy [33])
- traditional readability formulas (e.g., Flesch Reading Ease, Dale Chall Score)
- syntactic and coherence measures (e.g., clause ratio)
- semantic metrics (e.g., latent semantic analysis (LSA) magnitude) [17, 23, 25]
Using these variables, several models (e.g., random forest, elastic net) were trained and assessed for their ability to identify math word problems where less-skilled readers’ performance was lower than expected given baseline rates for similar problems while controlling for content area [27]. Variables in this study were included based on their relative importance within each category across multiple models and include:
- Word Count: Total number of tokens identified by
NLTK’sword_tokenize()function [11] - Average Sentence Length (ASL): Mean number of words per sentence
- Type-token Ratio: Ratio of unique lemmas to total
words calculated using
spaCy’s [20]en_core_web_lgpipeline for lemmatization and token classification. - Shannon Entropy: \(H = -\sum _{i=1}^{n} p_i \log _2(p_i)\), where \(p_i\) is the probability of word
\(i\) appearing in the text, calculated as the frequency of
the word (according to
FreqDistinNLTK) divided by the total number of words in the text. - Flesch Reading Ease: \(206.835 - 1.015 \times \text {ASL} - 84.6 \times \text {ASW}\), where ASW is average syllables per word [16, 22].
- New Dale-Chall Score: \(0.1579 \times (\frac {\text {difficult words}}{\text {words}} \times 100) + 0.0496 \times \text {ASL}\) where difficult words are words which do not occur in a corpus of 3,000 frequent words [12].
- Clause Ratio: Ratio of dependent to total clauses.
- LSA Magnitude: Euclidean norm of the 100 dimensional custom LSA embedding (TF–IDF+Truncated SVD) on our 31,008-problem corpus. Higher values indicate the text aligns more with topics and semantic patterns in the corpus.1
4. DATA & ANALYSIS
4.1 Observational Data Analysis
Student-level statistical models (e.g., a linear regression model detailed in Section 5.1) will enable us to consider reading ability and behaviors related to gaming the system as they relate to each other and learning outcomes, while lesson-level models will help us understand contextual factors related to readability of content and how they may be related to student behavior.
Beginning with the set of middle school students using MATHia during the 2023-24 school year in a school district in Massachusetts, we consider the set of 3,361 students for whom student-level end-of-year standardized math scores were available on the Massachusetts Comprehensive Assessment System (MCAS) exam and who completed the introductory lesson in MATHia. To this set of students, we apply the gaming detector model briefly described above to data from 443 lessons that track student mastery of KCs. To attempt to replicate previously established correlations between a proxy for reading ability and gaming behavior [30], we consider the extent to which reading ability (inferred by our prediction model) is correlated with students’ overall relative frequency of detected gaming. This is defined at the student-level as the proportion of their interaction “clips” on which the detector predicts that a student is engaged in gaming-related behavior. We then consider the extent to which these student-level factors predict end-of-year math MCAS scores.
At the lesson-level, we consider whether the relative frequency of detected gaming is different, overall, in lessons that have substantial reading (“reading lessons”) compared to those that do not (“non-reading lessons”). Next, we consider the 134 reading lessons completed by students in our dataset. We build prediction models of gaming frequency at the lesson-level that consider the readability factors for each lesson we described in the previous section. We estimate a separate model for students likely to be experiencing reading difficulties (ER) to compare to a model for students less likely to be experiencing reading difficulty (non-ER). Finding modest predictive links between readability and gaming the system tendencies, we move on to re-analyze recently collected experimental data.
4.2 Experimental Data Analysis
A recent randomized study tested whether lesson content in MATHia that had been re-written according to a style guide for added clarity and enhanced readability improved performance within two similar math lessons [1]. We focus on the Grade 7 lesson (“Analyzing Models of Two-Step Linear Relationships”) for which results were especially pronounced for ER (i.e., those in the bottom of quartile of predictions made by the reading prediction model). Specifically, students predicted to be ER who were enrolled in the lesson with the rewritten problems were able to master the content at a 13% higher rate and did so in 30% less time compared to students who were enrolled in the lesson with the original problems [1]. There were also improvements for students who were not predicted to be ER, although they were much less pronounced. Improvements for a similar 8th grade lesson (focusing on rational numbers instead of integers) were also less pronounced. Detailed in Table 1, 8,036 students completed the original (control) and experimental (“re-write”) content variants in this lesson across MATHia’s user base during the experiment in the 2022-23 school year.
For our current study, we performed a secondary analysis of data from this experiment to (a) replicate the finding of a relationship between “gaming” behavior and reading ability and (b) to test the novel hypothesis that improved readability of the texts would decrease gaming the system behavior. That is, we considered whether (presumably decreased) rates of behavior associated with gaming the system could potentially explain improvements, especially for ER, found in the experiment. We take the first step in establishing this association to determine if gaming behavior did in fact decline as a result of the intervention.
We first test the correlation between predicted reading ability and relative frequency of detected gaming via Pearson’s correlation to see if similar patterns to those in the observational data are present. We then compare differences in detected gaming frequency across experimental condition and predicted reading ability using the Mann-Whitney U test. We report results in the following section.
| Condition | Reading Prediction | \(n\) |
|---|---|---|
| Control | Emerging | 988 |
| Control | Non-Emerging | 2979 |
| Re-Write | Emerging | 1018 |
| Re-Write | Non-Emerging | 3051 |
5. RESULTS
5.1 Observational Data Analysis
Over the set of 3,361 students for whom we have reading ability predictions and estimates of overall relative frequency of gaming behavior, we find a negative correlation, illustrated in Figure 1, between predicted reading ability and relative frequency of detected gaming (r = -.352, 95% CI [-.375, -.328], p < .001). Students predicted to have better reading abilities (i.e., those with greater inferred probabilities of success on an ELA exam) tend to engage in less behavior associated with gaming the system. These results replicate a similar finding from previous research, which found a positive correlation between the assistance required in an introductory lesson (i.e., number of errors made and hints requested, which is greater for students presumed to be of lower reading ability) and detected gaming behavior [30].
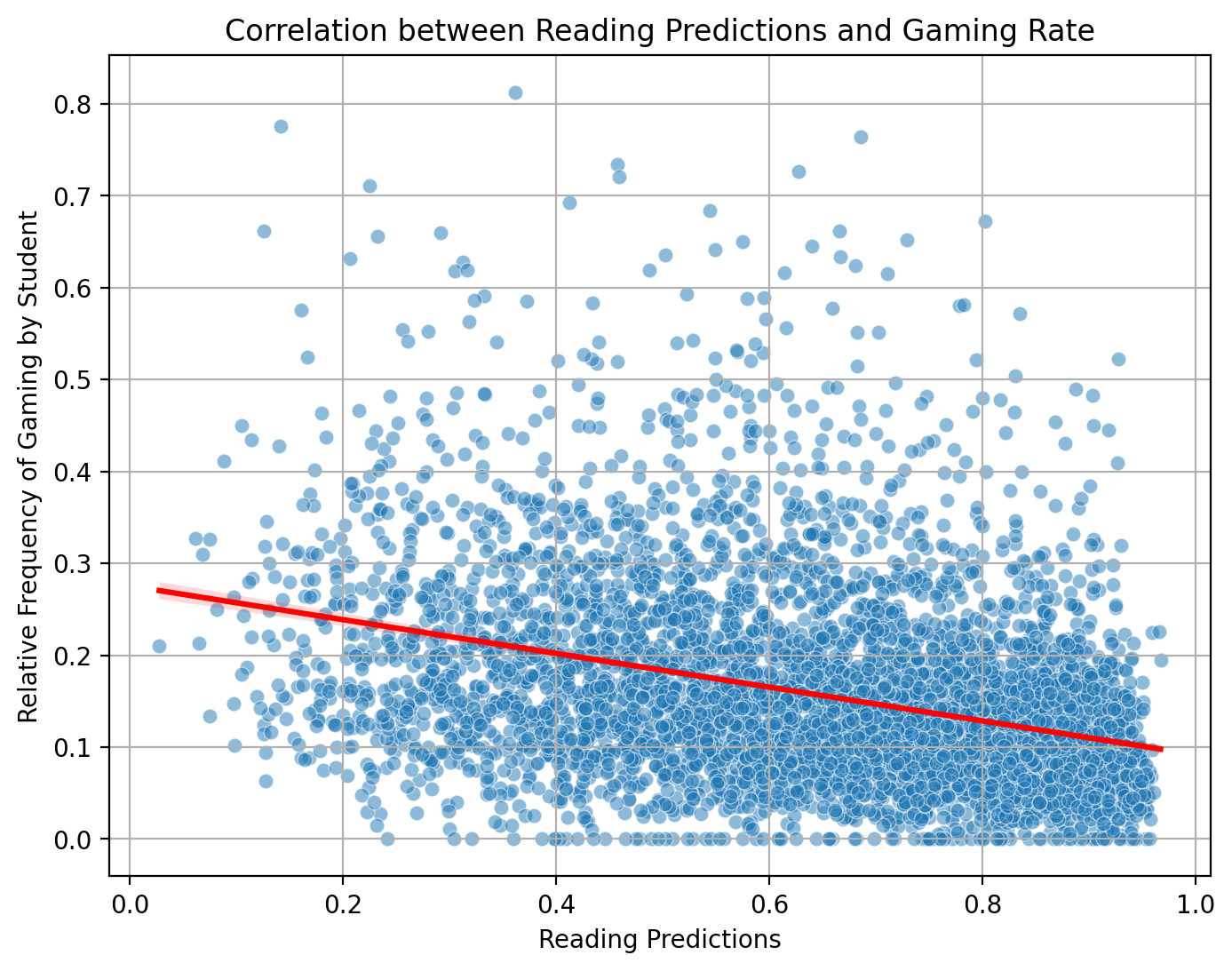
Not only are reading ability and detected gaming the system behavior correlated with each other, but both are also significantly correlated with a math learning outcome external to the MATHia platform, namely the MCAS math score. Table 2 summarizes the results of an ordinary least squares linear regression model predicting MCAS math outcomes with predicted reading ability and relative frequency of gaming behavior at the student-level. Consistent with prior findings [29, 3], we find that these two variables are both significant predictors of standardized math test outcomes and together account for 38.4% of the variance in this outcome.
| Variable | \(\beta \) | \(p\) |
|---|---|---|
| Gaming Frequency | -0.37 | <.001 |
| Reading Prediction | 0.39 | <.001 |
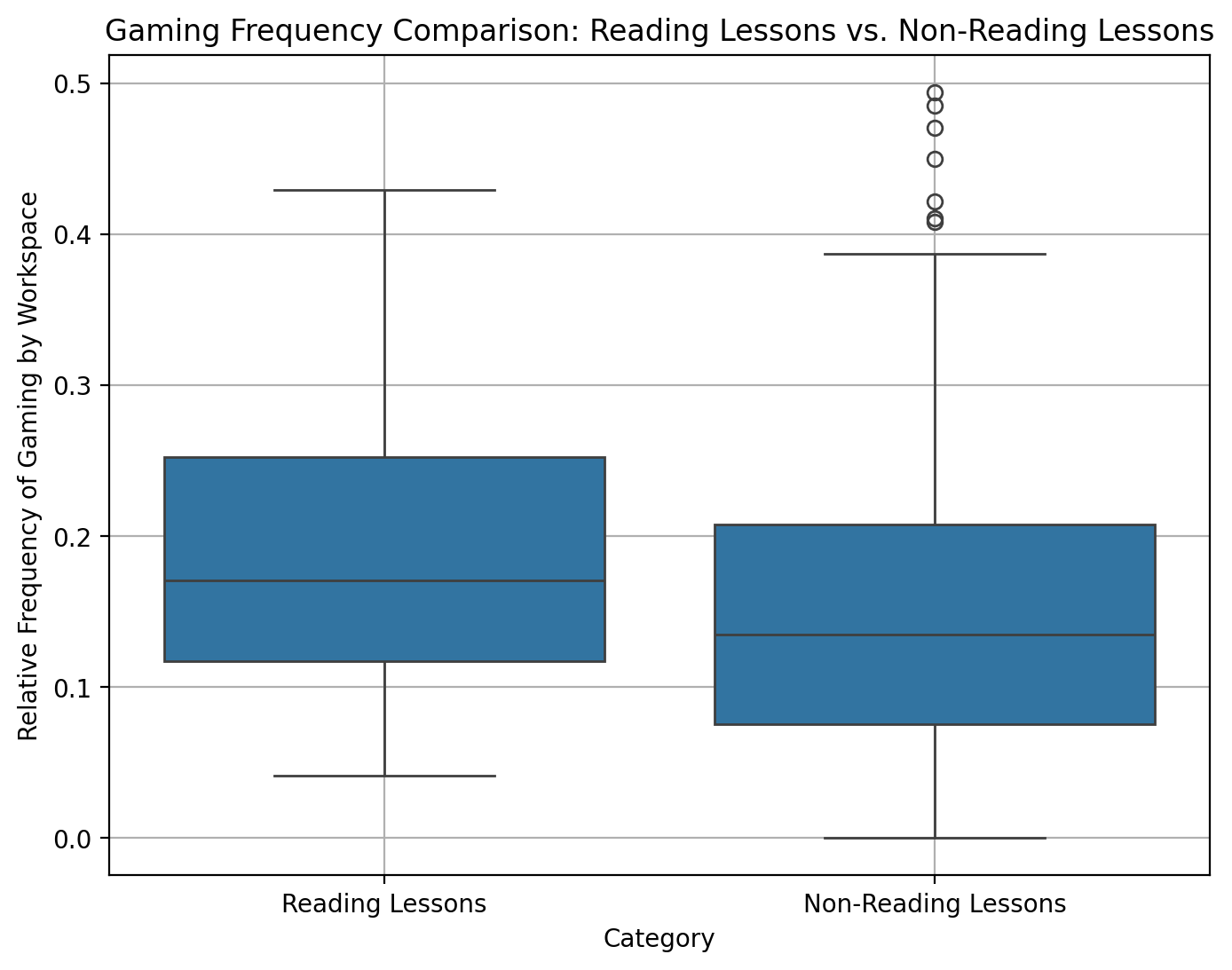
Next, we consider lesson-level analyses, starting with comparing math lessons containing substantial amounts of reading (reading lessons) to those lessons that do not (non-reading lessons). The mean relative frequency of detected gaming was greater in reading lessons (19%) compared to non-reading lessons (15%). Mann-Whitney U test indicates a significant difference in gaming frequency between the groups (W = 25732, p < .001). Figure 2 illustrates box plots for the distribution of mean relative frequency of detected gaming for students completing each lesson for the 134 reading lessons and 309 non-reading lessons in the data set from the Massachusetts school district in 2023-24. This suggests that students are more likely to engage in behavior associated with gaming the system in math lessons with substantial reading. Coupled with our finding that students who may be experiencing reading difficulties (i.e., those with lower predicted reading ability) are overall more likely to engage in gaming behavior, this raises the question whether particular aspects of the math lessons with substantial reading are associated with students’ tendency to engage in gaming-related behavior. Moreover, are there differences in the association of readability features with gaming for the two populations of ER and non-ER?
We consider lesson-level models over 134 lessons with substantial text (or reading lessons), for which we calculate the set of readability metrics described in Section 3. We specify and estimate ordinary least squares linear regression models separately for frequency of gaming behavior among ER and non-ER, summarizing our estimated models in Table 3. Three readability metrics (Word Count, Shannon Entropy, and Flesch Reading Ease) emerge as significant predictors of gaming among ER, while only two of these metrics are significant predictors of gaming among non-ER. In general, the patterns of association across the two models are similar, but we do find the model for non-ER explains greater variance (20%) in gaming frequency compared to the model for ER (14%).
| ER | non-ER | |||
|---|---|---|---|---|
| Variable | \(\beta \) | \(p\) | \(\beta \) | \(p\) |
| Clause Ratio | 0.05 | .64 | 0.08 | .44 |
| Custom LSA Magnitude | 0.11 | .36 | 0.08 | .50 |
| Dale-Chall Score | -0.20 | .38 | 0.0 | .99 |
| Flesch Reading Ease | -0.30 | .03 | -0.25 | .07 |
| Type-token Ratio | -0.20 | .29 | -0.24 | .18 |
| Sentence Length | -0.14 | .40 | -0.10 | .55 |
| Shannon Entropy | 0.50 | .001 | 0.49 | .001 |
| Word Count | -0.54 | .003 | -0.51 | .003 |
5.2 Experimental Data Analysis
Moving on to consider data from the previously reported experiment in the Grade 7 math lesson entitled “Analyzing Models of Two-Step Linear Relationships,” we find a negative correlation between predicted reading ability and relative frequency of detected gaming (r = -.27, 95% CI [-.29, -.25], p < .001), replicating the results found in the observational data for this particular lesson. Next, we tested whether there is a difference in detected gaming frequency between conditions across ER and non-ER (Figure 3). We find a small but significant difference in detected gaming frequency between conditions among non-ER (treatment condition: M = .076 (7.6%); control condition: M = .084 (8.4%); Cohen’s d = 0.08, 95% CI [0.02, 0.13]; Mann-Whitney U: W = 11619302, p < .001). Figure 3 illustrates these differences in gaming frequency by condition for ER and non-ER.
While the original experiment found that ER performed better in the re-written lessons, working in this re-written content did not affect the rate of gaming the system behavior among these students, so decreases in behavior associated with gaming the system do not appear to explain the much improved performance of ER in this prior experiment. Interestingly, there was a decrease in gaming the system behavior among non-ER in the re-written lessons. Future work should investigate the nature of this relationship between math problem readability and gaming behavior among students who are not likely to be experiencing reading difficulty.

6. DISCUSSION & CONCLUSION
This study contributes to our understanding of relationships among gaming the system behavior, reading ability, and math performance. We find a negative correlation between reading ability and gaming the system behavior; students with lower predicted reading ability are more likely to engage in behaviors associated with gaming the system. These findings are robust across two datasets, one observational and one experimental, from thousands of students, two school years, and hundreds of math lessons. We explored associations between readability characteristics of lesson content and detected gaming the system behavior frequency in that content. We find that a set of three readability features are significant predictors of gaming frequency for ER, and that two of these features are significant predictors of gaming among non-ER. Perhaps surprisingly, we find that readability features account for greater variance in gaming frequency for non-ER than for ER, suggesting that content readability could be more important for the decision to engage in gaming related behavior for students who are less likely to experience reading difficulty. This finding is supported by our subsequent re-analysis of data from a recent experiment that targeted readability enhancements to math lesson content. We found that non-ER engage in fewer gaming behaviors in the re-written (presumably more “readable”) lessons compared to the original while we find no difference in relative frequency of detected gaming behavior across experimental conditions for ER.
The readability metrics which predicted behaviors associated with gaming the system may reveal important considerations for understanding the readability of math word problems. First, higher Flesch Reading Ease predicted significant declines in gaming behaviors. This finding is encouraging given that reading ease is a widely known and readily available formula. Second, higher word count predicted a decrease in gaming behaviors.2 Attempts to improve text readability sometimes involve shortening the text (e.g., [19]), but the findings here suggest that this should be approached with caution. Shorter texts may pose a challenge to readers if they contain unfamiliar phrases or vocabulary, whereas longer texts may provide contextual supports to aid comprehension. Finally, higher Shannon entropy (i.e., less predictable texts) predicted increased gaming behaviors. To our knowledge, Shannon entropy has not been previously used as a measure of readability. The metric was selected following a search for text processing metrics that could explain text readability [27] where it emerged as an important identifier of word problems in which ER struggled more than expected. That it also explains variance in gaming behaviors highlights the need to look outside the standard stack of readability metrics to better understand how we can evaluate text readability of math problems.
Readability metrics are significant predictors of gaming for ER and non-ER. However, these metrics account for less variance in gaming behavior for ER, and an intervention targeting improved readability appears to have led to decreased gaming among non-ER but had no impact on gaming for ER. An “asset oriented” [28] framing of this finding could suggest that ER may be engaging in strategic forms of exploration of MATHia’s support. Future data-driven research might consider whether there are particular contexts (e.g., in particular lessons, parts of particular lessons, or even at particular KCs within lessons) where such behavior may be especially helpful (or at least “non-harmful” [7]), despite the overall negative correlation of these kinds of behavior with outcomes like math test scores that are found in the present study as well as in past research (e.g., [29, 15]). New approaches to modeling gaming the system (e.g., [21]) provide opportunities for exploring modeling various contextual factors related to lesson content that may prove fruitful.
Future detector modeling work can be informed by new approaches to qualitative and quantitative field observations and/or more nuanced approaches to automated log replays [6] to generate training data for such models. Efforts might focus specifically on learners likely to be experiencing reading difficulties to better understand how it is they are engaging with learning environments like ITSs and using the support provided by these systems in such ways that manifest as increased relative frequency of detected gaming behavior (using current detector models). Such observations may inform our notions of the construct of gaming the system itself and provide fresh insights into nuances of student behavior in adaptive learning systems. Such work may inform both the overarching constructs for which detector models are developed as well as the feature engineering from rich process data from software logging that serve as the input for detector models, regardless of the target construct.
7. ACKNOWLEDGMENTS
This material is based upon work supported by the National Science Foundation under Grant No. 2000638. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. The authors thank Ryan S. Baker, Clara Belitz, Nigel Bosch, Haejin Lee, Nidhi Nasiar, Jaclyn Ocumpaugh, and Steve Ritter for technical support and discussion related to this work.
8. REFERENCES
- H. Almoubayyed, R. Bastoni, S. R. Berman, S. Galasso, M. Jensen, L. Lester, A. Murphy, M. Swartz, K. Weldon, S. E. Fancsali, J. Gropen, and S. Ritter. Rewriting Math Word Problems to Improve Learning Outcomes for Emerging Readers: A Randomized Field Trial in Carnegie Learning’s MATHia. In N. Wang, G. Rebolledo-Mendez, V. Dimitrova, N. Matsuda, and O. C. Santos, editors, Artificial Intelligence in Education. Posters and Late Breaking Results, Workshops and Tutorials, Industry and Innovation Tracks, Practitioners, Doctoral Consortium and Blue Sky, volume 1831 of Communications in Computer and Information Science, pages 200–205. Springer Nature Switzerland, Cham, 2023.
- H. Almoubayyed, S. Fancsali, and S. Ritter. Generalizing predictive models of reading ability in adaptive mathematics software. In M. Feng, T. Käser, and P. Talukdar, editors, Proceedings of the 16th International Conference on Educational Data Mining, 2023.
- H. Almoubayyed, S. E. Fancsali, and S. Ritter. Instruction-embedded assessment for reading ability in adaptive mathematics software. In Proceedings of the 13th International Conference on Learning Analytics and Knowledge, LAK ’23, New York, NY, USA, 2023. Association for Computing Machinery.
- R. S. Baker. Is gaming the system state-or-trait? educational data mining through the multi-contextual application of a validated behavioral model. In Proceedings of the Workshop on Data Mining for User Modeling at the 11th International Conference on User Modeling, pages 76–80, 2007.
- R. S. Baker, A. T. Corbett, K. R. Koedinger, and A. Z. Wagner. Off-task behavior in the cognitive tutor classroom: when students "game the system". In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, CHI ’04, page 383–390, New York, NY, USA, 2004. Association for Computing Machinery.
- R. S. Baker and A. M. J. A. de Carvalho. Labeling student behavior faster and more precisely with text replays. In Proceedings of the 1st International Conference on Educational Data Mining, pages 38–47, 2008.
- R. S. J. d. Baker, A. T. Corbett, K. R. Koedinger, S. Evenson, I. Roll, A. Z. Wagner, M. Naim, J. Raspat, D. J. Baker, and J. E. Beck. Adapting to when students game an intelligent tutoring system. In M. Ikeda, K. D. Ashley, and T.-W. Chan, editors, Intelligent Tutoring Systems, pages 392–401, Berlin, Heidelberg, 2006. Springer Berlin Heidelberg.
- R. S. J. d. Baker, A. T. Corbett, K. R. Koedinger, and I. Roll. Generalizing detection of gaming the system across a tutoring curriculum. In M. Ikeda, K. D. Ashley, and T.-W. Chan, editors, Intelligent Tutoring Systems, pages 402–411, Berlin, Heidelberg, 2006. Springer Berlin Heidelberg.
- R. S. J. d. Baker, A. M. J. B. De Carvalho, J. Raspat, V. Aleven, A. T. Corbett, and K. R. Koedinger. Educational software features that encourage and discourage “gaming the system”. In Proceedings of the 2009 Conference on Artificial Intelligence in Education, pages 475–482, NLD, 2009. IOS Press.
- C. Belitz, H. Lee, N. Nasiar, S. E. Fancsali, S. Ritter, H. Almoubayyed, R. S. Baker, J. Ocumpaugh, and N. Bosch. Hierarchical dependencies in classroom settings influence algorithmic bias metrics. In Proceedings of the 14th Learning Analytics and Knowledge Conference, LAK ’24, page 210–218, New York, NY, USA, 2024. Association for Computing Machinery.
- S. Bird, E. Klein, and E. Loper. Natural language processing with Python: analyzing text with the natural language toolkit. O’Reilly Media, 2009.
- J. S. Chall and E. Dale. Readability revisited: The new Dale-Chall readability formula. Brookline Books, 1995.
- M. Cocea, A. Hershkovitz, and R. S. J. d. Baker. The impact of off-task and gaming behaviors on learning: Immediate or aggregate? In Proceedings of the 2009 Conference on Artificial Intelligence in Education, Frontiers in Artificial Intelligence and Applications, pages 507–514. IOS Press, 2009.
- A. T. Corbett and J. R. Anderson. Knowledge tracing: Modeling the acquisition of procedural knowledge. User Modeling and User-Adapted Interaction, 4(4):253–278, 1994.
- S. E. Fancsali. Causal discovery with models: Behavior, affect, and learning in Cognitive Tutor Algebra. In Proceedings of the 7th International Conference on Educational Data Mining, pages 28–35, 2014.
- R. Flesch. A new readability yardstick. Journal of applied psychology, 32(3):221, 1948.
- P. W. Foltz, W. Kintsch, and T. K. Landauer. The measurement of textual coherence with latent semantic analysis. Discourse processes, 25(2-3):285–307, 1998.
- K. J. Grimm. Longitudinal Associations Between Reading and Mathematics Achievement. Developmental Neuropsychology, 33(3):410–426, Apr. 2008.
- R. Helwig, M. A. Rozek-Tedesco, G. Tindal, B. Heath, and P. J. Almond. Reading as an access to mathematics problem solving on multiple-choice tests for sixth-grade students. The Journal of Educational Research, 93(2):113–125, 1999.
- M. Honnibal, I. Montani, S. Van Landeghem, and A. Boyd. spaCy: Industrial-strength Natural Language Processing in Python. 2020.
- Y. Huang, S. Dang, J. E. Richey, P. Chhabra, D. R. Thomas, M. W. Asher, N. G. Lobczowski, E. A. McLaughlin, J. M. Harackiewicz, V. Aleven, and K. R. Koedinger. Using latent variable models to make gaming-the-system detection robust to context variations. User Modeling and User-Adapted Interaction, 33(5):1211–1257, 2023.
- J. P. Kincaid, R. P. Fishburne Jr, R. L. Rogers, and B. S. Chissom. Derivation of new readability formulas (automated readability index, fog count and flesch reading ease formula) for navy enlisted personnel. Technical report, Naval Technical Training Command Millington TN Research Branch, 1975.
- W. Kintsch, D. S. McNamara, S. Dennis, and T. K. Landauer. Lsa and meaning: In theory and application. In Handbook of latent semantic analysis, pages 479–492. Psychology Press, 2007.
- K. R. Koedinger, A. T. Corbett, and C. Perfetti. The knowledge-learning-instruction framework: Bridging the science-practice chasm to enhance robust student learning. Cognitive Science, 36(5):757–798, 2012.
- T. K. Landauer and S. T. Dumais. A solution to plato’s problem: The latent semantic analysis theory of acquisition, induction, and representation of knowledge. Psychological review, 104(2):211, 1997.
- N. Levin, R. S. Baker, N. Nasiar, S. E. Fancsali, and S. Hutt. Evaluating gaming detector model robustness over time. In Proceedings of the 15th International Conference on Educational Data Mining, pages 398–405. International Educational Data Mining Society, 2022.
- K. Norberg, H. Almoubayyed, and S. Fancsali. Linguistic features predicting math word problem readability among less-skilled readers. In Proceedings of the 18th International Conference on Educational Data Mining (EDM 2025), Palermo, Sicily, Italy, July 2025. International Educational Data Mining Society. Accepted; to appear.
- J. Ocumpaugh, R. D. Roscoe, R. S. Baker, S. Hutt, and S. J. Aguilar. Toward asset-based instruction and assessment in artificial intelligence in education. International Journal of Artificial Intelligence in Education, 34(4):1559–1598, 2024.
- Z. A. Pardos, R. S. Baker, M. O. San Pedro, S. M. Gowda, and S. M. Gowda. Affective states and state tests: Investigating how affect and engagement during the school year predict end-of-year learning outcomes. Journal of Learning Analytics, 1:107–128, 2014.
- J. E. Richey, N. G. Lobczowski, P. F. Carvalho, and K. Koedinger. Comprehensive Views of Math Learners: A Case for Modeling and Supporting Non-math Factors in Adaptive Math Software. In I. I. Bittencourt, M. Cukurova, K. Muldner, R. Luckin, and E. Millán, editors, Artificial Intelligence in Education, volume 12163 of Lecture Notes in Computer Science, pages 460–471. Springer International Publishing, Cham, 2020.
- J. E. Richey, J. Zhang, R. Das, J. M. Andres-Bray, R. Scruggs, M. Mogessie, R. S. Baker, and B. M. McLaren. Gaming and confrustion explain learning advantages for a math digital learning game. In Artificial Intelligence in Education: 22nd International Conference, AIED 2021, Utrecht, The Netherlands, June 14–18, 2021, Proceedings, Part I, page 342–355, Berlin, Heidelberg, 2021. Springer-Verlag.
- S. Ritter, J. R. Anderson, K. Koedinger, and A. T. Corbett. Cognitive tutor: Applied research in mathematics education. Psychonomic Bulletin & Review, 14:249–255, 2007.
- C. E. Shannon. A mathematical theory of communication. The Bell system technical journal, 27(3):379–423, 1948.
- B. Shih, K. R. Koedinger, and R. Scheines. A response-time model for bottom-out hints as worked examples. In C. Romero, S. Ventura, M. Pechenizkiy, and R. S. Baker, editors, Handbook of Educational Data Mining. CRC Press, Boca Raton, FL, 2010.
- P. M. Vilenius-Tuohimaa, K. Aunola, and J. Nurmi. The association between mathematical word problems and reading comprehension. Educational Psychology, 28(4):409–426, July 2008. Publisher: Routledge _eprint: https://doi.org/10.1080/01443410701708228.
- M. Österholm. Characterizing Reading Comprehension of Mathematical Texts. Educational Studies in Mathematics, 63(3):325–346, Nov. 2006.
1This custom, domain-specific metric
consistently outperformed general-purpose embeddings in
feature-importance rankings (e.g., spaCy’s en_core_web_lg
or Google News Word2Vec)[27].
2Word count’s negative relationship with gaming behavior exists even when excluding co-variates from the model.
© 2025 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.