ABSTRACT
We propose a novel method for automated short answer grading (ASAG) designed for practical use in real-world settings. The method combines LLM embedding similarity with a nonlinear regression function, enabling accurate prediction from a small number of expert-graded responses. In this use case, a grader manually assesses a few responses, while the remainder are scored automatically—a common scenario when graders need to review some responses to feel confident assigning final grades. The proposed method achieves an RMSE of 0.717 outperforming the fine-tuned state-of-the-art transformer models in grading accuracy, which are more labor-intensive and computationally demanding, limiting their practicality for many applications. This method stands out for its ease of implementation and effectiveness, offering reliable accuracy with minimal effort. The code is made public.
Keywords
1. INTRODUCTION
Grading student answers to open questions is a still challenging task to automate. It generally requires the involvement of a domain expert for the result to be considered reliable. This requirement is often a deterrent to open questions in quizzes and exams administered to large groups. Indeed, open questions are very rarely graded in MOOCs (Massive Open Online Courses) where student cohorts can be in the hundreds and even thousands. Yet, this format of questions offers a rich means to assess knowledge because, contrary to Multiple Choice Questions, it goes beyond a recognition task and requires the generation of an answer. And while current LLM can automate verbal feedback on the quality of a student answer, quantitative grading provides an unambiguous assessment that verbal feedback lacks. Answer grading is irreplaceable not only for the purpose of determining a score of an exam or of a course, but also for visualizing learning progress, using thresholds to determine whether the student is prime to move on to another learning level, etc. Therefore, advances in Automatic Short Answer Grading (ASAG) is key to improving learning environments such as found in MOOCS. It is also highly desirable tool to assist instructors in colleges and universities in particular.
In this paper, we focus on ASAG as a tool to assist grading, as opposed to fully automate the process. We assume the grader will grade a few answers and expect the tool to complete the job. This assumption is realistic to the extent that, in a typical exam correction scenario, the grader is often compelled to correct a few answers to a single question in order to refine the grading criteria, make sure these criteria covers the span of valid answers, and to “calibrate” level of severity. This step is particularly relevant if an instructor needs to provide clear guidelines for other graders who assist in the task of grading. It also often helps the instructor refine the desired answer.
In this context, we propose an approach that draws upon a few graded answers to define a regression function that maps a similarity measure between the student and the desired answer to a grade. We use a recent transformer architecture to obtain a similarity measure and a Gaussian interpolation method to account for the non linearity of the mapping function.
The results obtained with a widely used dataset for evaluating ASAG model performance, Mohler’s data [15], show comparable precision to those achieved by fine-tuned transformer models. The proposed approach is particularly simple to implement and relies on calculations that are significantly more efficient in terms of computational time than fine-tuned models.
2. RELATED WORK
In recent years, the field of ASAG has been particularly fertile due to advancements in large language models (LLMs), which are based on transformer architectures. Most recent studies rely on pre-trained transformer models for text vectorization. By vectorizing both the expected answer and the student’s response, a semantic similarity calculation provides an indicator of the response’s validity [6, 8, 7, 10]. Amur et al. [3] conducted a review of numerous studies that adopted this approach for text similarity calculation in general, including its applications in ASAG. The proposed approach here falls into this category with relatively comparable results to those approaches that use fine-tuning.
In fact, several recent studies use fine-tuning of transformer models for classification [12, 11, 21, 9]. Garg et al. [11] used pairs of expected answers and student responses for transformer fine-tuning and achieved results exceeding other approaches with an RMSE of 0.732 on the Mohler data [15], which we use in this study. Zhu et al. [21] performed fine-tuning using a small portion of student responses to achieve the best Pearson correlation score with the same data, 0.8971. Finally, let’s mention the study by Agarwal et al. [1], which uses a deep learning approach with graphs and achieves an RMSE of 0.76 on the Mohler dataset.
Among the most recent works, a noteworthy set of studies use generative AI to directly request a score from the AI. The results of Chang et al. [5] and Grévisse [13] demonstrate significant improvements over earlier versions of generative AI models like ChatGPT, suggesting a promising avenue, though the authors of these two studies agree on the need for continued evaluator supervision. Tobler et al. [18] present an AI-generated tool designed to evaluate student responses by comparing them to reference answers. Other studies show that generative AI can provide useful feedback [2] and is also usable for enhancing alternative approaches [16, 4, 20]. However, these studies do not provide comparable results on the Mohler dataset and metrics.
3. GRADING WITH SEMANTIC SIMILARITY AND GAUSSIAN SMOOTHING
Akin to several approaches, our proposed method primarily relies on semantic similarity between the reference and the student answers and it relies transformer-generated embeddings. We refer to it as SemSimGrad. However, it distinguishes itself by assuming that a grader will provide a few pre-scored answers for each question to guide the correction process. While this requirement is a step away from full automation, initial grading has advantages. It allows to better gauge question difficulty and establish an adequate calibration of how strict the correction should be. It can also permit refinement of the reference answer based on unanticipated valid explanations.
The proposed approach involves calculating the cosine
similarity between embeddings of reference and student
answers. This similarity constitutes the input to a non-linear
regression function that will map it to a final grading, which in
the case of the Mohler dataset is on a [0–5] scale. The
details of how the regression function is determined are
given below and the code of the experiments is available at
https://osf.io/69eum/?view_only=1f36bde28c3c498ab96dbd1f02c8f378.
Let the set of pairs of scores associated with \(n\) student answers be defined as:
where \(S\) is the set of semantic similarity scores computed as the cosine similarity between a reference answer embedding a student answer embedding, and \(H\) is the set of human graded answer scores.
The goal is to define a function that maps an arbitrary similarity score, \(s\), to a grading, \(g\), given the data \(D\). Let this function be:
There are a number of possible solutions and we explored a few that perform smoothing or convolution over the given answer grades to obtain what we can consider a regression curve. They yield similar performances.
The simplest one is to define a function that takes a weighted sum of human graded scores in \(D\) that have corresponding semantic scores closest to the target grade \(s\). The closer the semantic scores are, the higher the weight.
We used a function similar to a kernel Gaussian smoothing function to determine the weight between semantic distances:
The function \(f(s)\) becomes:
where \(D_{\textrm {nei}}\) is the set of neighbourgs we keep (pairs in \(D\) with \(s_i\) closest to \(s\)). In our experiment, we chose to keep the full set of pairs in \(D\) since it contains only 15 graded answers.
The function \(f(s)\) performs what can be considered a regression with a smoothed curve over the data \(D\). The smoothing alleviates the large differences that can occur between the neighbouring values \(h\) used in the weighted sum. Smoothing is controlled by the parameter \(\sigma \). A large \(\sigma \) value will tend towards a flat regression line, whereas a small value will tend towards a regression line connecting values of \(h_i\) directly. Optimizing sigma to minimize the RMSE loss yields an optimal value of 0.046 for the 15 graded answers condition.
It is important to note that a regression function, \(f(s)\), is calculated on a per question basis. In other words, \(f(s)\) is in fact \(f(s,D)\) and \(D\) is specific to each question. Indeed, the distribution of scores varies significantly from one question to another (see Section 4 below and Figure 3) and the fiting \(f(s)\) to each question can achive better accuracy than a fit to all questions. This observation underscores the motivation behind creating a model tailored to each question rather than a single general model for the entire exam.
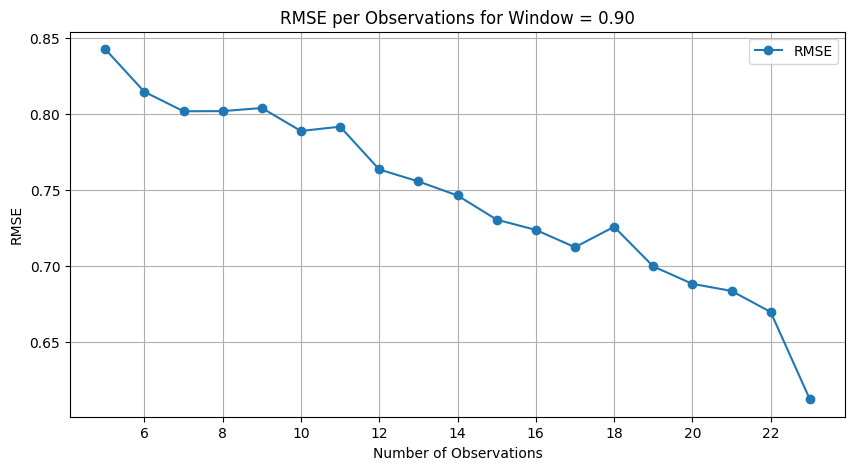
Another important observation is that the accuracy of SemSimGrad increases with the number of given answer grades as we will see in Figure 2.
4. DATASET
Our experiments are run on the Mohler dataset [15], which is a reference for evaluating short answer correction systems (ASAG) [3, 10]. It consists of 80 questions and 2,273 student responses, each scored on a scale of 0 to 5 by two instructors. The data originates from an introductory computer science course at a Texas university. The average length of the reference answers ranges between 15 to 20 words.
Figure 1 illustrates the distribution of scores for 2,273 responses according to their similarity with their respective expected answers. Each data point is an answer on the grade-similarity space. A significant number of responses are scored 5/5 and relatively few fall below a score of 4/5. As can be seen from this figure, the correlation remains relatively weak and suggests that attempting to build a regression model based on the global grades-similarity data is doomed to provide unreliable results, especially in the low similarity scores.
The variability of relations between grade and similarity is further demonstrated in Figure 3 (at end of paper). Akin to Figure 1, each data point is an answer on the grade-similarity scale, but the results are shown over a few individual questions taken to illustrate the types of distribution we find. Each questions has around 30 answers. Noteworthy is that these distributions vary considerably from one question to another. For example, questions 2 (1.2 in the dataset) and 3 (1.3) have a low correlation rate, whereas questions 4 (1.4) and 78 (12.7) have a very high success rate, leading to highly variable correlation calculations based on the sampling. Given the unique characteristics of each distribution, it is more effective to model a distribution specific to one question rather than using an overall model. We delay the discussion of other details in this figure as we return to it in the next section ( 5).
5. EXPERIMENTS
The general methodology of the experiments involves creating a regression function with which to compute a grade from an answer’s similarity score. The regression is obtained according to the procedure described in section 3 and data from 15 student grades and similarity scores. The remaining answers are used to measure the performance.
Each of the 2,273 student responses is associated with an expected answer. A language model was used to encode each response into a vector with a typical length ranging from a few hundred to several thousand numbers for larger models. Subsequently, cosine similarity is computed between these vectors as the measure of similarity. No data preprocessing was performed.
Table 1 presents various statistics on the LLM used for
phrase encoding that were studied. Our choice focused on
mxbai-embed-large and text-embedding-3-small from
OpenAI. After experimenting with a few LLM, we find they
provide the most accurate and efficient encoding. Encoding
speed of 100 answers takes approximately one a second using an
Apple M4 processor.
A sample of 15 responses out of 30 was selected for each question, with uniform sampling: after sorting the responses by similarity, selections is equally spread across the similarity range to ensure good coverage.
In order to provide more insights into the results of the regression modeling, Figure 3 shows example of regression functions constructed from smoothed gradings as explained in section 3 (omitting the extrapolation to similarities 0 and 1). The solid red dots represents the given grades used to construct the regression curve (solid black line), whereas the blue ones are the unobserved gradings used to compute the prediction accuracy. For each question, we show the value of the correlation and RMSE values.
| Model | Correlation | # Parameters (m) | Quan. | Vec. | Time | Year |
|---|---|---|---|---|---|---|
| all-minilm-l6-v2 | 0.482 | 22.6 | – | 384 | 0.5s | 2021 |
| bge-m3 | 0.517 | 576.6 | 16 | 1024 | 1.2s | 2024 |
| mxbai-embed-large | 0.523 | 334 | 16 | 1024 | 1.2s | 2024 |
| text-embedding-3-small | 0.538 | – | – | 1536 | 1.5s | 2024 |
6. RESULTS
The table 2 presents the performance of our proposed model, SemSimGrad, in terms of correlation and RMSE. These results are compared with those from state-of-the-art approaches. The best performances are indicated in bold.
We also investigated the evolution of the performance as a
function of the number of given grades provided for construction
the regression curve. Figure 2 illustrates the variation of the
RMSE as a function of the number graded answers for the
text-embedding-3-small LLM. The RMSE values exhibit a
decreasing trend as the number of observations increases,
reaching an RMSE near 0.60 when the number of grades given
is 23. Note that the figure stops at 23 observations because
24 is the minimal number of answers for the the Mohler
dataset.
| Approach | Type | Correlation | RMSE |
|---|---|---|---|
| SemSimGrad (our approach) | |||
| mxbai-embed-large* | Sem. sim. | 0.623 | 0.726 |
| text-embedding-3-small* | Sem. sim. | 0.550 | 0.717 |
| State of the art | |||
| [11] | BERT + Sem. sim. | 0.777 | 0.732 |
| [1] | Graph + transformer | na | 0.762 |
| [16] | IAG+Sem. sim. | 0.735 | 0.779 |
| [21] | BERT + LSTM. | 0.897 | 0.827 |
| Baseline approaches | |||
| [17] | BOW | 0.592 | 0.887 |
| [14] | BOW | na | 0.999 |
| * Performance at 15 graded answers given per question.
| |||
text-embedding-3-small).
7. DISCUSSION
Let us first observe that the performance varies considerably
depending on whether correlation or RMSE is taken as a
performance measure. While we reported correlation in this
work for the sake of completeness, we consider it is not a
reliable measure, at least for the Mohler data and for the reason
we argue in this paragraph. For example, assume the following
predicted scores to five answers, \(g\), and their corresponding
observed grades, \(h\):
| \(g\) | = | ( | 4.91, | 4.92, | 4.9, | 4.9, | 4.9) | predicted |
|---|---|---|---|---|---|---|---|---|
| \(h\) | = | ( | 5 , | 4.5 , | 5 , | 5 , | 5 ) | observed |
These predictions should be considered good, yet the correlation
between \(g\) and \(h\) is -0.88. However, the RMSE is very good
at 0.21. Such anomaly can occur as shown in Figure 3 for
question 31 and 51. They have weak correlations because
almost all scores are perfect (5/5). Considering the frequent
number of questions that have close to perfect scores, this
anomaly in the correlation score is susceptible to make the
correlation an unreliable measure of performance. Furthermore,
questions such as 46 has a perfect RMSE, but a correlation that
cannot be computed because all scores are 5. A related issue
occurs with question 55 where the test cases have a null
variance, even though the given answers’ variance is not
null.
Therefore, our analysis will only focus on the RMSE score which can arguably be considered more reliable than the correlation.
By retaining only RMSE, the SemSimGrad method outperforms the state of the art. Considering that it is much less computationally intensive and simpler than fine-tuning-based approaches [1, 11, 21], it thus appears to be a viable choice.
In this paper, we achieved an RMSE of 0.717 using 15 graded samples as training data points. While 15 answers make up half of the responses in the Mohler dataset, it is important to note that the accuracy would be the same regardless of the number of remainign answers to grade. In a larger classroom setting with over 100 students, we would expect to achieve similar RMSE performance. Grading just a small subset and automatically predicting the remaining scores makes the approach a practical and efficient solution. A key consideration is ensuring that the selected graded samples are distributed uniformly with respect to similarities. In a larger class, if 15 graded answers are chosen in this manner,
It is worth mentioning, however, that the paraphrasing approach for expected responses [16] might compare favorably to SemSimGrad in terms of simplicity since it does not require model fine-tuning. The principle involves generating multiple versions of expected answers using generative AI to improve the evaluation of student responses. However, for this study, the performance of RMSE remains advantageous over SemSimGrad.
8. CONCLUSION AND FUTURE WORK
We propose a method that offers the advantage of performance in terms of precision. It is also highly resource-efficient compared to other state-of-the-art approaches that require fine-tuning, and it is easy to implement. However, it requires manual correction of about 15 responses per question. In fact, results show that the greater the number of manual grading is provided to the approach, the more accurate it is. Therefore, the number of manual gradings to provide really depends on the grader’s tolerance to inaccuracies.
However, we argue that the manual correction step for calibration or model refinement may be an unavoidable step of the grading process. Considering that a relatively reliable grading can be obtained with around 15 manual corrections, this approach is particularly useful for larger classes.
Yet, whether the manual correction of a portion of the responses is unavoidable or not, the responsibility for having reliable corrections still rests with the individual doing the corrections. Therefore, the next step in this exploratory study is to determine to what extent the approach can identify automatic evaluations that are reliable versus those that require verification.
9. REFERENCES
- R. Agarwal, V. Khurana, K. Grover, M. Mohania, and V. Goyal. Multi-relational graph transformer for automatic short answer grading. In M. Carpuat, M.-C. de Marneffe, and I. V. Meza Ruiz, editors, Proceedings of the 2022 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pages 2001–2012, Seattle, United States, July 2022. Association for Computational Linguistics.
- D. Aggarwal, P. Bhattacharyya, and B. Raman. "I understand why I got this grade": Automatic short answer grading with feedback, 2024.
- Z. H. Amur, Y. Kwang Hooi, H. Bhanbhro, K. Dahri, and G. M. Soomro. Short-text semantic similarity (stss): Techniques, challenges and future perspectives. Applied Sciences, 13(6):3911, 2023.
- D. Carpenter, W. Min, S. Lee, G. Ozogul, X. Zheng, and J. Lester. Assessing student explanations with large language models using fine-tuning and few-shot learning. In Proceedings of the 19th Workshop on Innovative Use of NLP for Building Educational Applications (BEA 2024), pages 403–413, 2024.
- L.-H. Chang and F. Ginter. Automatic short answer grading for Finnish with ChatGPT. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 38, pages 23173–23181, 2024.
- A. Condor, M. Litster, and Z. Pardos. Automatic short answer grading with sbert on out-of-sample questions. International Educational Data Mining Society, 2021.
- E. Del Gobbo, A. Guarino, B. Cafarelli, and L. Grilli. GradeAid: a framework for automatic short answers grading in educational contexts—design, implementation and evaluation. Knowledge and Information Systems, 65(10):4295–4334, 2023.
- A. Divya, V. Haridas, and J. Narayanan. Automation of short answer grading techniques: Comparative study using deep learning techniques. In 2023 Fifth International Conference on Electrical, Computer and Communication Technologies (ICECCT), pages 1–7, 2023.
- T. Firoozi, O. Bulut, C. D. Epp, A. Naeimabadi, and D. Barbosa. The effect of fine-tuned word embedding techniques on the accuracy of automated essay scoring systems using neural networks. Journal of Applied Testing Technology, pages 21–29, 2022.
- S. K. Gaddipati, D. Nair, and P. G. Plöger. Comparative evaluation of pretrained transfer learning models on automatic short answer grading. arXiv preprint arXiv:2009.01303, 2020.
- J. Garg, J. Papreja, K. Apurva, and G. Jain. Domain-specific hybrid BERT based system for automatic short answer grading. In 2022 2nd International Conference on Intelligent Technologies (CONIT), pages 1–6. IEEE, 2022.
- H. A. Ghavidel, A. Zouaq, and M. C. Desmarais. Using BERT and XLNET for the automatic short answer grading task. In CSEDU (1), pages 58–67, 2020.
- C. Grévisse. Llm-based automatic short answer grading in undergraduate medical education. BMC Medical Education, 24(1):1060, 2024.
- M. Mohler, R. Bunescu, and R. Mihalcea. Learning to grade short answer questions using semantic similarity measures and dependency graph alignments. In D. Lin, Y. Matsumoto, and R. Mihalcea, editors, Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies, pages 752–762, Portland, Oregon, USA, June 2011. Association for Computational Linguistics.
- M. Mohler and R. Mihalcea. Text-to-text semantic similarity for automatic short answer grading. In A. Lascarides, C. Gardent, and J. Nivre, editors, Proceedings of the 12th Conference of the European Chapter of the ACL (EACL 2009), pages 567–575, Athens, Greece, Mar. 2009. Association for Computational Linguistics.
- L. Ouahrani and D. Bennouar. Paraphrase generation and supervised learning for improved automatic short answer grading. International Journal of Artificial Intelligence in Education, pages 1–44, 2024.
- M. A. Sultan, C. Salazar, and T. Sumner. Fast and easy short answer grading with high accuracy. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pages 1070–1075, 2016.
- S. Tobler. Smart grading: A generative ai-based tool for knowledge-grounded answer evaluation in educational assessments. MethodsX, 12:102531, 2024.
- C. N. Tulu, O. Ozkaya, and U. Orhan. Automatic short answer grading with semspace sense vectors and malstm. IEEE Access, 9:19270–19280, 2021.
- S.-Y. Yoon. Short answer grading using one-shot prompting and text similarity scoring model, 2023.
- X. Zhu, H. Wu, and L. Zhang. Automatic short-answer grading via BERT-based deep neural networks. IEEE Transactions on Learning Technologies, 15(3):364–375, 2022.
1We omit the results of [19] here because they use a different metric which does not allow for comparison.
© 2025 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.