ABSTRACT
Automatic question generation (AQG) for mathematics education remains an elusive goal for Intelligent Tutoring Systems and educators. While pre-trained transformer-based language models have significantly advanced natural language generation, they often struggle to precisely control problem complexity and cognitive demands. In this paper, we introduce a collaborative multi-agent framework as a novel method of incorporating inference-time computation into AQG. This approach leverages multiple agents that iteratively refine generated question-answer pairs to better balance complexity and cognitive demand. We evaluate the generated questions on five meta-evaluation criteria: relevance, importance, clarity, difficulty matching, answerability, to assess the system’s ability to control the required complexity and quality of the questions. Preliminary evaluations show that this collaborative multi-agent framework elevates the quality of generated educational content by fostering a more nuanced balance between cognitive challenge and clarity. These promising outcomes suggest that integrating collaborative multi-agent workflows can yield more controlled, pedagogically valuable content that can help advance automated educational content generation and adaptive learning environments.
Keywords
1. INTRODUCTION AND RELATED WORK
Dynamically generating mathematics practice exercises and
homework problems is a longstanding challenge for Intelligent
Tutoring Systems (ITS) and educators [5]. Typically, educators
and ITS either rely on existing problems or create new
variations through minor modifications. Automatic Question
Generation (AQG) aims to address this challenge but faced
limited early success [5, 22]. Over time, diverse AQG methods
have emerged, including the fine-tuning of pretrained language
models for topic-controlled question generation [10] [17],
often leveraging contrastive examples (examples of similar
questions that differ in topic) to help the model distinguish
and generate questions suited to specific concepts. More
recently, prompt engineering guided by Bloom’s Taxonomy
[1], few-shot prompting with chain-of-thought reasoning
[15, 1], and contextualized math word problem generation
with equation constraints [7, 19] have further advanced the field. Modern ITS require robust AQG capabilities
to dynamically provide personalized practice problems,
effectively intervening in students’ learning trajectories [14].
An ITS system can be conceptualized as managing a student’s
knowledge state. Figure 1 illustrates a typical ITS architecture
where a knowledge-tracing module continuously monitors
student comprehension across various Knowledge Components
(KCs). At each interaction, the ITS selects a KC based on the
student’s knowledge state and using a Curriculum Designer
module, commonly implemented via reinforcement learning
(RL) models or search algorithms like expectiminimax [14], to
present an appropriate problem as an intervention. This
adaptive process supports personalized curricula aimed at
continuously enhancing student mastery of KCs. Consequently,
ITS must be capable of dynamically generating practice
problems for any KC, leveraging heuristics from example
problems and incorporating difficulty assignment mechanisms.
.png)
The AQG task can vary significantly based on system
requirements. For instance, [1] utilizes Large Language
Models (LLM) prompted explicitly by textbook chapters
and related question sets, while other systems may rely
solely on textbook chapters without additional prompts.
Another common variation is concept-based generation,
where AQG systems create questions derived directly from
explicitly defined concepts or knowledge graphs. This paper
approaches AQG from an ITS perspective, defining inputs
as: 1) the KC name per Common Core State Standards
definitions, 2) a set of example questions for that KC, and
3) the required difficulty level (easy, medium, or hard).
The system outputs a generated question and its answer.
AQG aligns with broader natural language generation (NLG)
challenges, particularly the lack of definitive ground truths and
the subjective nature of human evaluations. Because of this,
evaluating NLG has been a key area of recent research, giving
rise to frameworks like G-Eval [12], which leverages GPT-4 as a
reference-free evaluator for tasks such as summarization,
demonstrating improved alignment with human judgments.
However, biases may persist in these LLM-based evaluation
methods, as highlighted by [8, 18]. Task-specific initiatives
like QGEval [4] reveal continued difficulties in ensuring
strong alignment between automated metrics and human
ratings in question generation, underscoring the broader
challenges posed by subjectivity and the absence of definitive
ground truth. Another major ongoing challenge in AQG is
ensuring high-quality questions that are coherent, relevant,
and accurately aligned with the intended difficulty level.
To address these issues, we explore recent advancements in
LLMs, particularly in Inference Time Computation (ITC)
techniques [16]. ITC generally refers to methods that extend or
refine a model’s outputs during deployment without additional
training, by orchestrating extra computational steps, retrieving
context, or allowing models to interact with each other. Within
this paradigm, we focus on multi-agent collaborative systems,
also known as agentic workflows [20], which improve LLM
performance by facilitating interactions between multiple
agents. This allows them to debate, complement each other’s
strengths, and incorporate diverse perspectives. Of all
the agent collaboration techniques, debate emerges as a
particularly effective approach, inspired by the concept of the
Society of Mind [13] to harness collective knowledge. Studies
show that multi-agent debate can enhance factuality and
reasoning [3], foster divergent thinking [11], and even achieve
state-of-the-art performance in mathematical reasoning [20].
Other lines of work focus on mechanisms such as hierarchical or
roleplaying-based collaboration [22, 2] and competitive settings
[21], while recent frameworks like AutoGen [20], Camel [9], and
MetaGPT [6] facilitate a variety of multi-agent collaboration
structures. By enabling agents to engage in structured
interactions, these workflows enhance factual accuracy,
reasoning capabilities, and the overall quality of generated
questions.
In this paper, we investigate the potential of integrating ITC
techniques through collaborative multi-agent frameworks into
AQG. We evaluate the outputs based on clarity, relevance, importance, answerability, and difficulty matching. Our
contributions are three-fold. First, we propose two novel
collaborative frameworks specifically designed for AQG tasks.
Second, we develop a self-curation method for AQG guided by
cognitive demand criteria from Bloom’s taxonomy. Third, we
introduce an automated evaluation framework to assess
automatically generated math questions, considering clarity,
relevance, importance, answerability, and difficulty control. Our
research explores two key questions:
(1) Does difficulty matching depend on the proposed difficulty?
(2) Do agentic workflows improve question generation compared
to baseline models?
2. METHOD AND EXPERIMENT SETUP
We propose two multi-agent systems that generate a question and answer based on a given difficulty level, set of examples, and the KC name for use in the ITS. In this section, we will explain the data, agents, multi-agent workflows, prompting strategies, curation method, and evaluation metrics of the system.
2.1 Data
Our experiments utilize the Problem Bodies 1 dataset. The dataset is an extension of the ASSISTments dataset, a widely used benchmark from ITS. Problem Bodies contains middle-school math questions accompanied by empirical student performance metrics. Each question in this dataset includes a “percent correct" attribute, representing the percentage of students who answered correctly. This allows us to categorize the questions into easy, medium, and hard difficulty levels, providing an empirically grounded measure of difficulty aligned with real-world student performance.
2.2 Agents
In our experiments, we use the following agents/roles:
Teacher: Generates math questions and answers for a specific
KC at a set difficulty level. It returns concise responses while
adjusting based on conversation context.
Generic Critic: Provides objective, high-level feedback on clarity,
relevance, and difficulty alignment without introducing new
content. It references the overall discussion for consistent
evaluation.
Consensus CEO: Serves as the final decision-maker by reviewing
conversation history and selecting the best question-answer pair
from multiple agents. If a consensus exists, it reports that;
otherwise, it chooses the option aligning best with the KC,
difficulty requirements, and sample solutions.
Versatile Agent: Dynamically participates in collaborative
discussions, making one of three decisions based on chat history:
(1) generate a new Q&A pair, (2) revise an existing pair, or (3)
endorse a peer’s pair while providing constructive feedback.
This agent uses prior messages and examples to ensure its
contributions align with the KC, intended difficulty, and the
collective goal of reaching consensus.
2.3 Workflows and Experimental Setup
.png)
We systematically evaluated four distinct approaches, including
two Baseline scenarios and two agentic workflows (see Figure 2)
designed to generate educational math question-answer pairs,
each with varying complexity and collaborative structures:
Baseline Teacher Zero-Shot: This workflow uses a single
teacher agent using a zero-shot prompt approach to generate
self-contained math questions and answers without relying on
prior examples or conversation history.
Baseline Teacher Few-Shot: In this variant, the teacher agent is
guided by a few example question-answer pairs, aligning it more
closely with other few-shot-based workflows.
Teacher-Critic Cycle (TCC): TCC involves two agents: a teacher
generates an initial math question and answer, followed by
iterative critique from a generic critic agent. The critic assesses
clarity, relevance, difficulty, and pedagogical appropriateness,
with the teacher refining the content across multiple feedback
rounds. Experimentally, we varied the number of interaction
rounds between two to five, and evaluated the effectiveness of
two prompt engineering techniques: Auto Chain-of-Thought
(AutoCoT) and explicit Solution Generation, by enabling and
disabling them. In Solution Generation, the teacher (or versatile
agent) tries to output only the final answer to a math problem,
while in AutoCoT, the teacher (or versatile agent) uses a
step-by-step reasoning process before arriving at the final
answer.
Collective Consensus (CC): CC is a multi-agent workflow
involving a collaborative conversation to reach consensus on
math question-answer pairs. Initially, one versatile agent
generates a question-answer pair, after which two to four
versatile agents sequentially contribute by either creating a new
question, revising an existing question with feedback, or
explicitly agreeing with feedback. Decoding parameters,
including sampling seed and temperature, are randomized per
agent to encourage diverse perspectives. Following iterative
discussion (ranging from two to five rounds), a consensus CEO
agent reviews the conversation. If consensus is achieved,
the CEO selects the agreed-upon final pair; otherwise, it
chooses the best candidate based on collective judgment and
educational alignment. As with TCC, we explored the impact of
AutoCoT and explicit Solution Generation, evaluating their
roles both enabled and disabled. Across all workflows,
we tested three prompting strategies which we detail in
Section 2.4: Empirical Difficulty Prompting, Empirical
Prompting, and Simple Prompting. These strategies help assess
whether providing explicit difficulty-level context enhances
question quality relative to random or difficulty-specific
examples.
2.4 Difficulty Prompting Strategies
Empirical: All but the baseline use a few-shot approach. Math
questions are labeled “easy,” “medium,” or “hard” using real
student performance data (higher “percent correct" indicates
easier). These labeled examples guide the model in generating
questions matching the requested difficulty.
Prompting Empirical: This variant also relies on empirical
difficulty data but only presents examples matching the requested difficulty. For instance, if the model is asked to
produce an “easy” question, only empirically identified easy
examples are shown.
Prompting Simple (Random Examples): Here, the model receives
randomly selected examples from all difficulty tiers. It must rely
solely on the requested difficulty (“easy,” “medium,” or “hard”)
without explicit guidance from example labels, placing more
responsibility on general instructions.
2.5 Self-Curation
We design a Bloom Agent that assigns each output question a Bloom evaluation score (1–5) based on its cognitive demands, ensuring alignment with the three Bloom tiers—lower (Remembering, Understanding), middle (Applying, Analyzing), and upper (Evaluating, Creating). Because generating many candidate questions is computationally cheap, we aggressively discard those that fail the expected cognitive challenge, retaining only those demonstrating strong Bloom alignment. We also compare this curation method against Random Curation (RC) of our methods for comparison. Unlike conventional curation, which may rely on syntactic features, our approach prioritizes pedagogical rigor over mere textual similarity, ensuring that even a surplus of suboptimal questions yields a subset with meaningful cognitive depth.
2.6 Evaluation Metrics
To evaluate the generated questions, we used prompt engineering
to quantify the quality of each instance based on the following
criteria:
Relevance: Measures how well the generated questions align
with example questions and the targeted KC. Scored on a scale
of 1 (not relevant) to 5 (highly relevant).
Importance: Assesses whether the question emphasizes key
conceptual components of the targeted KC. Rated from 1 (least
important) to 5 (essential).
Clarity: Evaluates structural coherence and linguistic precision
of a question to ensure it is easily understood by middle-school
students. Scored from 1 (unclear) to 5 (exceptionally clear).
Difficulty Matching: Determines how well a question’s complexity
aligns with the specified difficulty level (easy, medium, hard).
Cognitive difficulty ranges from basic factual recall (easy) to
moderate conceptual reasoning (medium) and advanced
analytical skills (hard). Scored from 1 (no alignment) to 5
(perfect alignment).
Answerability: Evaluates whether a middle-school student can
reasonably understand and respond to the question based on
the provided information. Rated from 1 (unanswerable) to 5
(clearly answerable).
The prompts for the agents and the evaluation module can be found in our
repository 2
3. RESULTS AND DISCUSSION
| Method | Clarity | Relevance | Importance | Difficulty Matching | Answerability | Avg. Score |
|---|---|---|---|---|---|---|
| Baseline_ZS | 3.66 | 4.61 | 4.67 | 4.41 | 4.65 | 4.40 |
| Baseline_FS | 3.70 | 4.93 | 4.73 | 4.02 | 4.71 | 4.42 |
| CC_RC | 3.50 | 4.95 | 4.71 | 3.94 | 4.61 | 4.34 |
| TCC-RC | 3.72 | 4.90 | 4.73 | 4.11 | 4.79 | 4.45 |
| CC | 3.60 | 4.99 | 4.76 | 4.96 | 4.94 | 4.65 |
| TCC | 3.75 | 4.92 | 4.70 | 4.88 | 4.94 | 4.64 |
Table 1 shows the evaluation results of our methods, TCC and
CC, compared to both the baseline and non-curated agentic
methods. While TCC and CC outperform both the baselines
and their non-curated counterparts across all evaluation metrics,
the improvements are incremental rather than drastic. The
greatest gains are observed in Difficulty Matching and
Relevance, which suggests that incorporating iterative critique
and collective refinement enhances alignment with the intended
cognitive challenge and pedagogical quality. These findings
directly address Research Question 2 (RQ2). Additionally,
the fact that non-curated agentic methods underperform
the baseline suggests that agent-based generation alone is
insufficient without structured selection or refinement. Agent
responses exhibit greater variability, sometimes failing to meet
standards of clarity, difficulty alignment, or answerability. This
highlights the importance of iterative curation mechanisms to
ensure consistency and reliability in multi-agent AQG.
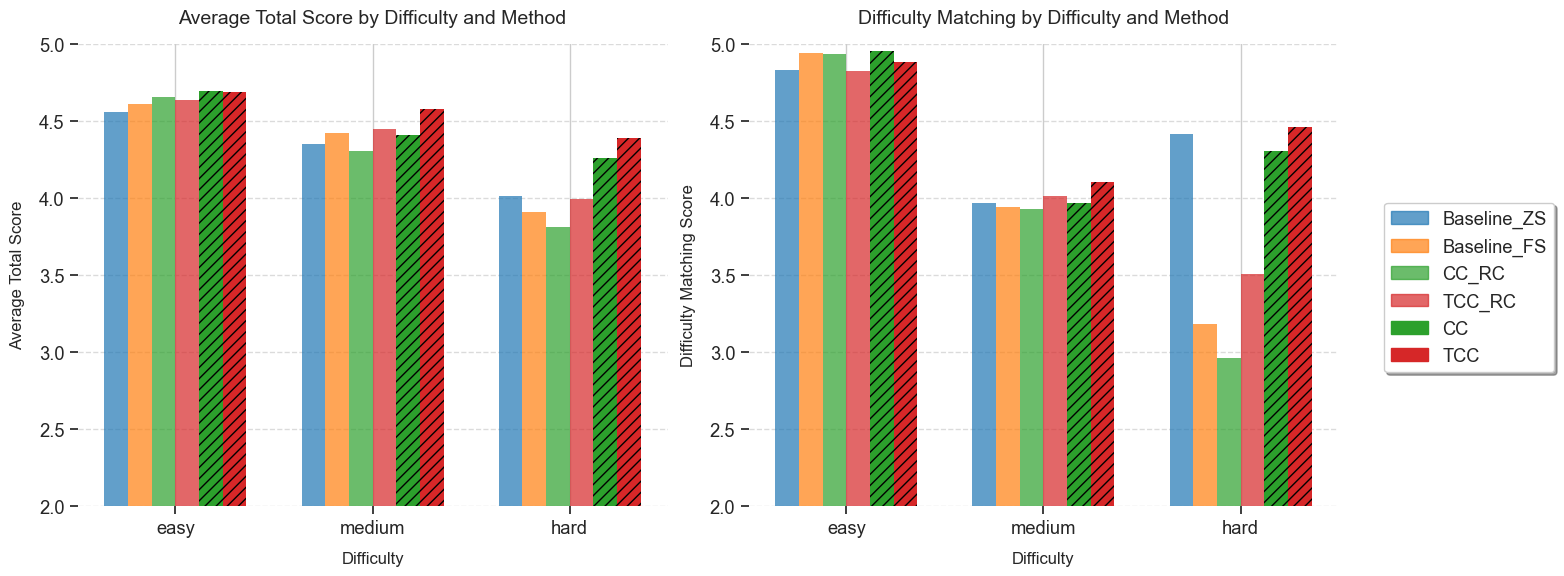
Figure 3 presents the Difficulty Matching and Average Score
across different difficulty levels (easy, medium, hard) for
each method. The trends observed align with the overall
evaluation results. Our curated methods (TCC and CC)
outperform the baselines and non-curated methods, though
the improvements remain incremental. A general pattern
emerges where both Difficulty Matching and Average Score
decrease as question difficulty increases. This finding addresses
Research Question 1 (RQ1). The observed trend suggests that
difficulty matching is indeed more challenging for harder
questions, indicating that LLM-based generation struggles to
maintain appropriate cognitive complexity as difficulty
increases. Notably, the baseline models and non-curated agentic
methods perform significantly worse on hard questions. This
reinforces the need for structured prompting and iterative
refinement to produce well-calibrated high-difficulty questions.
Unexpectedly, the Baseline Zero-Shot method achieves higher
Difficulty Matching scores than both the Baseline Few-Shot
model and several agentic methods (including curated and
non-curated variants), which suggests that few-shot examples
may introduce biases or inconsistencies in aligning questions
with intended difficulty. These findings underscore the intricate
interplay between prompting strategies and difficulty alignment,
prompting further study of how example-based prompts
shape model outputs. A key question involves how much
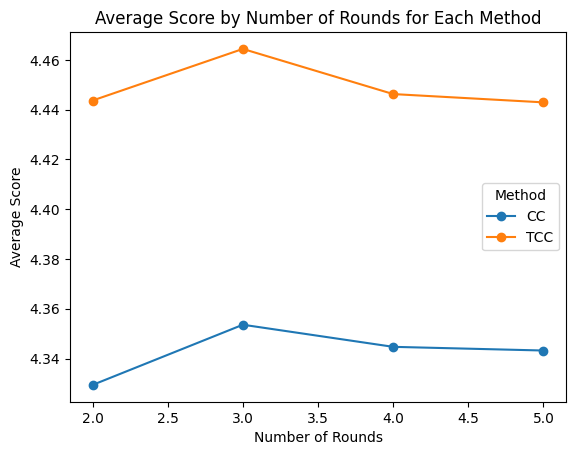
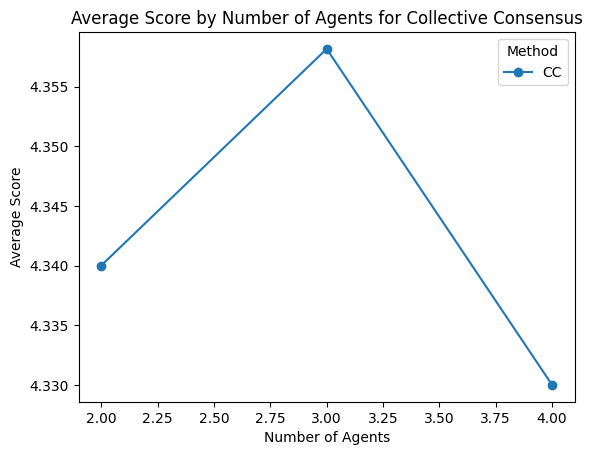
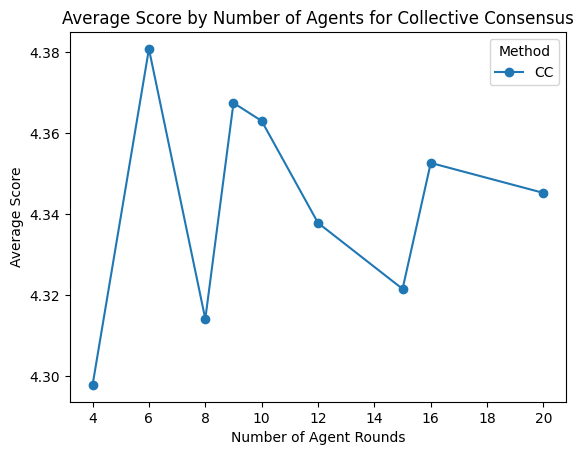
inference computation is optimal. Since these are iterative
ITC methods, merely increasing the number of rounds or
agents does not guarantee performance gains and can even
yield diminishing returns (Figure 4). Our limited settings
suggest that a more comprehensive parameter search is
needed to pinpoint where additional computation yields real
benefits.
Furthermore, our study finds that the effectiveness of prompting
strategies for enabling the in-context learning ability of LLMs is
minimal. As shown in Table 2, different few-shot prompting
techniques had little to no impact on performance. This
suggests that current few-shot learning strategies may be
suboptimal for the AQG task. Future research could explore
alternative prompt engineering and adaptive few-shot learning
techniques to better leverage in-context learning for question
generation.
Finally, a critical area for future work is the quality of evaluation itself. All our findings rely on automated evaluations
conducted by GPT-4 and based on state-of-the-art NLG
evaluation frameworks [12, 4], which raises concerns about
potential biases and limitations in LLM-based self-evaluation. In
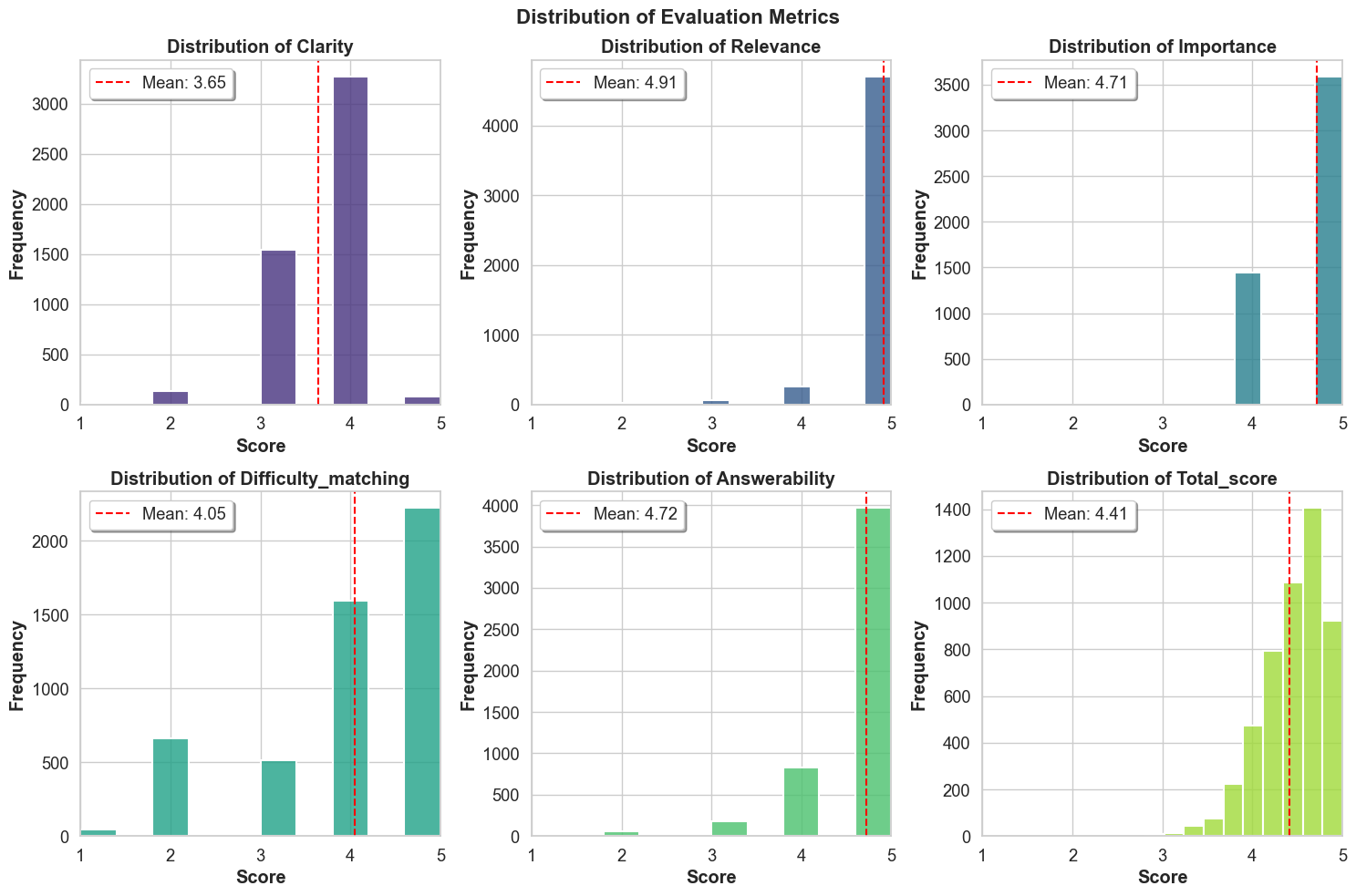
particular, we observed a ceiling effect (Figure 5) in the
resulting evaluation scores similar to what the G-Eval authors
reported. This effect can mask finer-grained differences in
system performance and limit the discriminative power of
LLM-based evaluations. If the evaluation system exhibits
misalignment with human judgment, all derived insights could
be affected. To address this, we plan to collect human
evaluation data and fine-tune our automated evaluation module
to align more closely with human evaluators and increase the
trustworthiness of the assessment process.
Overall, while our study demonstrates that the success of
difficulty matching is dependent on the proposed difficulty level
(RQ1) and that agentic workflows can improve question
generation compared to the baseline (RQ2), these improvements
come with important caveats. Optimization of inference
computation, refinement of few-shot learning strategies,
and enhancing evaluation reliability are key directions for
future research to advance AI-driven educational content
generation.
4. REFERENCES
- A. Blobstein, D. Izmaylov, T. Yifal, M. Levy, and A. Segal. Angel: A New Generation Tool for Learning Material based Questions and Answers. 2024.
- N. Chen, Y. Wang, Y. Deng, and J. Li. The Oscars of AI Theater: A Survey on Role-Playing with Language Models, Jan. 2025. arXiv:2407.11484 [cs].
- Y. Du, S. Li, A. Torralba, J. B. Tenenbaum, and I. Mordatch. Improving Factuality and Reasoning in Language Models through Multiagent Debate, May 2023. arXiv:2305.14325 [cs].
- W. Fu, B. Wei, J. Hu, Z. Cai, and J. Liu. QGEval: Benchmarking Multi-dimensional Evaluation for Question Generation. In Proceedings of the 2024 Conference on Empirical Methods in Natural Language Processing, pages 11783–11803, Miami, Florida, USA, 2024. Association for Computational Linguistics.
- M. Heilman and N. A. Smith. Good Question! Statistical Ranking for Question Generation. In R. Kaplan, J. Burstein, M. Harper, and G. Penn, editors, Human Language Technologies: The 2010 Annual Conference of the North American Chapter of the Association for Computational Linguistics, pages 609–617, Los Angeles, California, June 2010. Association for Computational Linguistics.
- S. Hong, M. Zhuge, J. Chen, X. Zheng, Y. Cheng, C. Zhang, J. Wang, Z. Wang, S. K. S. Yau, Z. Lin, L. Zhou, C. Ran, L. Xiao, C. Wu, and J. Schmidhuber. MetaGPT: Meta Programming for A Multi-Agent Collaborative Framework, Nov. 2024. arXiv:2308.00352 [cs].
- W.-Y. Hwang and I. Q. Utami. Contextualized and Personalized Math Word Problem Generation Using GPT and Authentic Contextual Recognition. In 2024 12th International Conference on Information and Education Technology (ICIET), pages 177–181, Yamaguchi, Japan, Mar. 2024. IEEE.
- R. Koo, M. Lee, V. Raheja, J. I. Park, Z. M. Kim, and D. Kang. Benchmarking Cognitive Biases in Large Language Models as Evaluators, Sept. 2024. arXiv:2309.17012 [cs].
- G. Li, H. A. A. K. Hammoud, H. Itani, D. Khizbullin, and B. Ghanem. CAMEL: Communicative Agents for "Mind" Exploration of Large Language Model Society, Nov. 2023. arXiv:2303.17760 [cs].
- Z. Li, M. Cukurova, and S. Bulathwela. A Novel Approach to Scalable and Automatic Topic-Controlled Question Generation in Education, Jan. 2025. arXiv:2501.05220 [cs].
- T. Liang, Z. He, W. Jiao, X. Wang, Y. Wang, R. Wang, Y. Yang, S. Shi, and Z. Tu. Encouraging Divergent Thinking in Large Language Models through Multi-Agent Debate, Oct. 2024. arXiv:2305.19118 [cs].
- Y. Liu, D. Iter, Y. Xu, S. Wang, R. Xu, and C. Zhu. G-Eval: NLG Evaluation using GPT-4 with Better Human Alignment, May 2023. arXiv:2303.16634 [cs].
- M. L. Minsky. The society of mind. Simon and Schuster, New-York, 1988.
- C. Piech, J. Spencer, J. Huang, S. Ganguli, M. Sahami, L. Guibas, and J. Sohl-Dickstein. Deep Knowledge Tracing, June 2015. arXiv:1506.05908 [cs].
- N. Scaria, S. D. Chenna, and D. Subramani. Automated Educational Question Generation at Different Bloom’s Skill Levels using Large Language Models: Strategies and Evaluation. volume 14830, pages 165–179. 2024. arXiv:2408.04394 [cs].
- C. Snell, J. Lee, K. Xu, and A. Kumar. Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters, Aug. 2024. arXiv:2408.03314 [cs].
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser, and I. Polosukhin. Attention Is All You Need, Aug. 2023. arXiv:1706.03762 [cs].
- Y. Wang, J. Yuan, Y.-N. Chuang, Z. Wang, Y. Liu, M. Cusick, P. Kulkarni, Z. Ji, Y. Ibrahim, and X. Hu. DHP Benchmark: Are LLMs Good NLG Evaluators?, Feb. 2025. arXiv:2408.13704 [cs].
- Z. Wang, A. S. Lan, and R. G. Baraniuk. Math Word Problem Generation with Mathematical Consistency and Problem Context Constraints, Sept. 2021. arXiv:2109.04546 [cs].
- Q. Wu, G. Bansal, J. Zhang, Y. Wu, B. Li, E. Zhu, L. Jiang, X. Zhang, S. Zhang, J. Liu, A. H. Awadallah, R. W. White, D. Burger, and C. Wang. AutoGen: Enabling Next-Gen LLM Applications via Multi-Agent Conversation, Oct. 2023. arXiv:2308.08155 [cs].
- Y. Zeng, Y. Wu, X. Zhang, H. Wang, and Q. Wu. AutoDefense: Multi-Agent LLM Defense against Jailbreak Attacks, Nov. 2024. arXiv:2403.04783 [cs].
- R. Zhang, J. Guo, L. Chen, Y. Fan, and X. Cheng. A Review on Question Generation from Natural Language Text. ACM Transactions on Information Systems, 40(1):1–43, Jan. 2022.
APPENDIX
A. ADDITIONAL FIGURES AND RESULTS
| Method | Difficulty Prompting Strategies | Difficulty Matching | Avg. Score |
|---|---|---|---|
| CC | empirical | 4.71 | 4.60 |
| CC | prompting empirical | 4.68 | 4.64 |
| CC | prompting simple | 4.70 | 4.61 |
| TCC | empirical | 4.66 | 4.66 |
| TCC | prompting empirical | 4.61 | 4.64 |
| TCC | prompting simple | 4.67 | 4.65 |
© 2025 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.