ABSTRACT

Knowledge Tracing models have been used to predict and understand student learning processes for over two decades, spanning multiple generations of student learners who have different relationships with the technologies used to provide them instruction and practice. Given that student experiences of education have changed dramatically in that time span, can we assume that the student learning process modeled by KT is stable over time? We investigate the robustness of four different KT models over five school years and find evidence of significant model decline that is more pronounced in the more sophisticated models. We then propose multiple avenues of future work to better predict and understand this phenomenon. In addition, to foster more longitudinal testing of novel KT architectures, we will be releasing student interaction data spanning those five years.

Keywords

1. INTRODUCTION

Since their introduction by Corbett and Anderson in 1994 [3], Knowledge Tracing (KT) models have been used in intelligent tutoring systems and online learning platforms (OLPs) to track student knowledge levels and predict future performance. As the use of student modeling techniques like KT becomes ever more ubiquitous, it is necessary to revisit the assumptions that guide our practice. We assume that data collected from different learners represents the same underlying learning process. We assume that the ways in which students learn that are measurable by scientists and practitioners remain consistent. Given the maturation of educational data mining (EDM) as a field and the availability of learner data spanning generations of learners, perhaps it is now possible to verify that our assumptions are correct, or at least to identify the circumstances where they are safe assumptions to make.

The educational best-practices of 20 years ago are obviously not the educational best-practices of the modern day. Educational policy has shifted towards meticulous measurement of student progress [6], identifying failing schools [14], and standardizing subject curricula to better facilitate rigorous measurement [20]. Simultaneously, OLPs rose in popularity, automating student practice and proliferating student engagement data [21, 7]. These educational platforms have also matured since their creation, and every pedagogical and cosmetic change to these platforms could impact the way students interact with these platforms. Even ignoring educational policy changes, students are individuals in a large and changing world, and world events which change how humans relate to one another impact students as much as anyone else. In a particularly extreme example, an entire generation of students experienced learning losses due to the COVID-19 pandemic [5]. In a changing world, how can we be sure our modeling techniques are still valid?

In this paper, we pose the following research questions about the stability and validity of KT models as they age:

1. Does the complexity of a KT model impact its susceptibility to concept drift?
2. Is it possible to detect when concept drift is happening from the data itself?
3. Can we use explainable AI techniques to explain why our KT models lose accuracy?

This work discusses our attempts to create a dataset able to answer these research questions. We borrow from Data Mining literature the concept of dataset shift, and discuss its applicability to OLPs. We then describe our data collection methods, taking steps to ensure that our datasets contain similar exercise banks and Knowledge Concepts. Next, we propose a methodology for evaluating KT models both within their temporal context and across student populations using the data we have collected. We then apply this methodology to four well-studied KT models and examine how each model performs outside of its temporal context. Finally, we discuss the results of this initial study, and propose future research directions to answer research questions 2-4.

2. BACKGROUND

In this section, we introduce and discuss literature relevant to our investigation of KT model robustness. First, we introduce KT as a specific machine learning task (Section 2.1). Next, we discuss frameworks for analyzing the drift of software systems from their original contexts (Section 2.2). Finally, we discuss relevant prior work investigating the generalization of KT models (Section 2.3).

2.1 Knowledge Tracing

Long established in EDM literature, KT is defined as a many-to-many time series binary classification problem attempting to predict the correctness of future student responses based on prior performance. Numerous machine learning architectures have been applied to this task, including Factorization Machines [23] and psychometric models like Item Response Theory [25]. Shen et al. [22] provides a comprehensive survey of historical and contemporary methods. In this work, we will be replicating four well-studied KT models: Bayesian Knowledge Tracing [3], Performance Factors Analysis [17], Deep Knowledge Tracing [19], and Self-Attentive Knowledge Tracing [15].

2.2 Distributional Shifts

Broadly speaking, for a given supervised learning problem with training set \(X\) and labels \(Y\), we are interested in modeling the joint probability distribution:

Changes in this joint distribution can be categorized based on the part of this distribution that changes [9]:

1. Covariate Shift, a change \(P(X)\) while \(P(Y|X)\) remains the same.
2. Label Shift, a change in \(P(Y)\) while \(P(X|Y)\) remains the same.
3. Concept Drift, a change in \(P(Y|X)\) while \(P(X)\) remains the same.

Concept drift is perhaps the most difficult of these three shifts to adapt to, since a supervised learning model explicitly attempts to estimate \(P(Y|X)\). Prior works have created methods to detect [10], explain [24], and adapt to [13] concept drift. More recently, researchers have investigated how concept drift can impact common EDM and learning analytics models. Levin et al. [12] explores how concept drift affects a variety of gaming detectors, finding that contemporary gaming detectors had more trouble generalizing to newer data than classic decision tree based methods, while Deho et al. [4] found that concept drift in LA models is linked to algorithmic bias. These works highlight two distinct ways of attempting to quantify concept drift: through longitudinal model evaluation and through the application of concept drift detectors to log data.

2.3 Prior Exploration of KT Generalizability

Covariate Shift, Label Shift, and Concept Drift all have the potential to decrease the performance of KT models. Covariate and/or label shift could be introduced by an influx of new students, or a new curriculum being added to an OLP. Since KT models explicitly try to model the acquisition of knowledge, identifying when a model is susceptible to concept drift simultaneously raises questions about the underlying learning process.

This paper is not the first published work investigating the impact of changing student populations on knowledge tracing models. Lee et al. [11] investigated the stability of BKT model predictions over time and found that, while BKT is generally stable year-over-year, large, sudden shifts in student populations can have deleterious effects on model robustness. We wish to replicate and extend these findings by investigating the performance of other well-known KT models, including BKT, when applied to student interaction data spanning a longer time frame.

3. PRELIMINARY WORK

3.1 Data Collection & Preparation

Data for this study was collected using the ASSISTments OLP [7], spanning the five academic years between 2019–2020 and 2023–2024. Data not suitable for conducting Knowledge Tracing was filtered out, consisting of all data collected in the months of June, July, and August, as well as problem logs for non-computer-gradable questions, and all problem logs from problem set assigned fewer than 100 times total during the five academic years of interest. Summer student populations often differ greatly to the population of students using an OLP during the school year, while non-computer-gradable problems are incompatible with standard KT models, and removing low-use problem sets from the data lowers the likelihood of models differing solely due to out-of-vocabulary KCs and exercises. The relative size of each year’s data is worthy of note. Different years have great differences in the number of available logs, with the largest year having over twenty-one times the amount of total problem logs. Since the amount of available training data has a large impact on model fitness, this disparity in dataset sizes presents an issue.

To mitigate the impact of our dataset sizes, rather than using all available data for each year, we draw random samples from each available academic year. Randomly sampling user/exercise interactions would isolate those rows from their surrounding context, while sampling per user reintroduces concerns over differences in training set sizes, as the total number of exercises completed per user varies widely. Instead, we randomly sample 50,000 assignment logs, which are instances of a single student completing an assigned problem set. This allows us to draw samples of consistent size, since problem set length is more consistent, while collecting coherent sequences of student/exercise interactions in their full context. Our final dataset consists of ten such samples¹ per academic year, with samples containing 50,000 assignment logs each².

3.2 Study Design

In order to effectively investigate the susceptibility of KT models to concept drift, we need to establish baseline performance for each model on each target year and somehow evaluate models in a cross-year context. To measure within-year performance, we conducted a ten-fold cross validation, training one model per sample and evaluating it on the other nine samples³. To investigate model performance across years, for each sample of a target year, we trained a model on the full sample and evaluated the fit model on one sample from all subsequent years. While it’s clearly possible to evaluate a model using data gathered before the training year, doing so is more of an analytical tool, as in real systems possibly affected by concept drift, model accuracy decreases due to the introduction of later data. Thus, we only evaluate models using data from their training year or later. Additionally, to explicitly investigate the effect of overparameterization on model performance over time, two different versions of SAKT were evaluated: one using KCs as model input and one using exercises directly.

3.3 Model Implementations

Each model was implemented in Python 3.12⁴, with the following differences. BKT was implemented with the forgetting parameter enabled via the hmmlearn package. After fitting models for each available KC in the training set, learned parameters were averaged to make a "best guess" KT model in the case of evaluating KCs that were not present in the training set. PFA was implemented using scikit-learn [18], fitting separate covariates for wins and fails for each KC, along with a KC level intercept and parameters for KCs not present in the training set. Both SAKT and DKT were implemented in pytorch [16] and trained on NVIDIA A100 GPUs.

3.4 Results

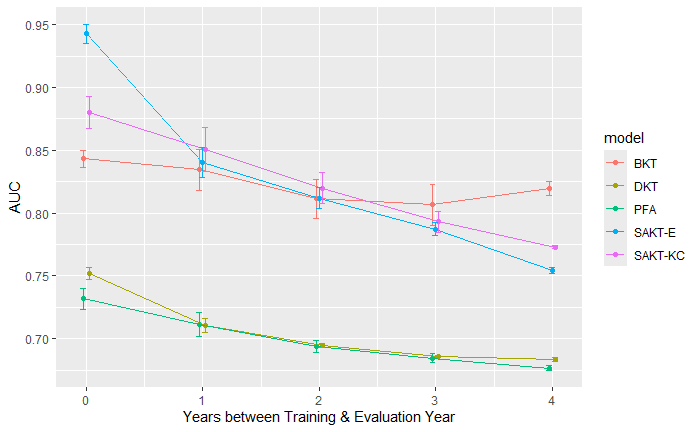
Model evaluation results can be found in figure 1 which shows the AUC of each model compared to the years since the model was trained organized by model. Every model tested by our method had decreasing AUC over time, with BKT having the most stable performance over time, and SAKT exhibiting the steepest decline in performance. In particular, SAKT-E experienced a very sharp decline just one year post-training, then steadily declines at a similar rate to SAKT-KC.

4. FUTURE DIRECTIONS

Our current work establishes that KT models are susceptible to concept drift, and that more complex models experience a more severe degradation of performance. Our current approach is limited in that we can only demonstrate the presence of concept drift after training KT models. This is a rather indirect way of measuring concept drift, and it provides little to no insight into the mechanism behind the drift we observe.

RQ2: Drift DetectionMultiple techniques exist to predict the presence of concept drift directly from data distributions [2]. Adapting these drift detectors to our longitudinal KT dataset and examining the relationship between samples with and without predicted drift may provide some insight into what specifically causes the drift we observe in educational data

RQ3: Model AnalysisWhile complex machine learning models are often treated as black boxes, the field of explainable AI has arisen in recent years to explain model decisions in human terms [8]. More specifically, the attention weights of self-attention models provide a rich source of information about a model’s decision process [1]. Applying these techniques to SAKT models could allow us to understand the specific mechanisms of model degradation they experience while also illuminating differences in the learning process between different cohorts of students.

With these future works, we aim to contribute to the use of machine learning to understand knowledge acquisition. While novel KT architectures are being proposed regularly, there is much more to understand about the contextual differences between student populations and the way these differences are reflected in trained KT models. With the public release of our longitudinal dataset, we will allow other researchers to subject their proposed models to the unique stresses posed by time in a way that was previously infeasible.

Acknowledgments

We would like to thank our many past and current funders including NSF (2118725, 2118904, 1950683, 1917808, 1931523, 1940236, 1917713, 1903304, 1822830, 1759229, 172-4889, 1636782, 1535428, 2215842, 2341948, & 2153481); IES (R305N210049, R305D210031, R305A170137, R305A170243, R305A180401, R305A120125, R305R220012, & R305T240029); GAANN (P200A120238, P200A180088, & P200A150306); DOE (U411B190024 S411B210024, & S411B220024); ONR (N00014-18-1-2768); NIH (via a SBIR R44GM146483), Schmidt Futures, BMGF, CZI, Arnold, Hewlett, the Jaffe Foundation, and anonymous donors. None of the opinions expressed here are those of the funders.

5. REFERENCES

1. S. Abnar and W. Zuidema. Quantifying attention flow in transformers. arXiv preprint arXiv:2005.00928, 2020.
2. F. Bayram, B. S. Ahmed, and A. Kassler. From concept drift to model degradation: An overview on performance-aware drift detectors. Knowledge-Based Systems, 245:108632, 2022.
3. A. T. Corbett and J. R. Anderson. Knowledge tracing: Modeling the acquisition of procedural knowledge. User Modeling and User-Adapted Interaction, 4(4):253–278, Dec. 1994.
4. O. B. Deho, L. Liu, J. Li, J. Liu, C. Zhan, and S. Joksimovic. When the Past != The Future: Assessing the Impact of Dataset Drift on the Fairness of Learning Analytics Models. IEEE Transactions on Learning Technologies, 17:1007–1020, 2024. Conference Name: IEEE Transactions on Learning Technologies.
5. R. Donnelly and H. A. Patrinos. Learning loss during Covid-19: An early systematic review. PROSPECTS, 51(4):601–609, Oct. 2022.
6. P. Hallinger and R. H. Heck. Exploring the journey of school improvement: classifying and analyzing patterns of change in school improvement processes and learning outcomes. School Effectiveness and School Improvement, 22(1):1–27, 2011.
7. N. T. Heffernan and C. L. Heffernan. The ASSISTments Ecosystem: Building a Platform that Brings Scientists and Teachers Together for Minimally Invasive Research on Human Learning and Teaching. International Journal of Artificial Intelligence in Education, 24(4):470–497, Dec. 2014.
8. A. Holzinger, A. Saranti, C. Molnar, P. Biecek, and W. Samek. Explainable ai methods-a brief overview. In International workshop on extending explainable AI beyond deep models and classifiers, pages 13–38. Springer, 2020.
9. C. Huyen. Designing Machine Learning Systems, chapter Data Distribution Shifts and Monitoring, pages 225–262. O’Reilly Media, 2022.
10. R. Klinkenberg and T. Joachims. Detecting concept drift with support vector machines. 2000.
11. M. P. Lee, E. Croteau, A. Gurung, A. F. Botelho, and N. T. Heffernan. Knowledge Tracing over Time: A Longitudinal Analysis. International Educational Data Mining Society, 2023. ERIC Number: ED630851.
12. N. Levin, R. Baker, N. Nasiar, F. Stephen, and S. Hutt. Evaluating Gaming Detector Model Robustness Over Time. Proceedings of the 15th International Conference on Educational Data Mining, International Educational Data Mining Society, Jan. 2022.
13. S. Madireddy, P. Balaprakash, P. Carns, R. Latham, G. K. Lockwood, R. Ross, S. Snyder, and S. M. Wild. Adaptive Learning for Concept Drift in Application Performance Modeling. In Proceedings of the 48th International Conference on Parallel Processing, ICPP ’19, pages 1–11, New York, NY, USA, Aug. 2019. Association for Computing Machinery.
14. M. Nicolaidou and M. Ainscow. Understanding Failing Schools: Perspectives from the inside. School Effectiveness and School Improvement, 16(3):229–248, Sept. 2005. Publisher: Routledge _eprint: https://doi.org/10.1080/09243450500113647.
15. S. Pandey and G. Karypis. A Self-Attentive model for Knowledge Tracing, July 2019. arXiv:1907.06837 [cs, stat].
16. A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Köpf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai, and S. Chintala. PyTorch: an imperative style, high-performance deep learning library. Curran Associates Inc., Red Hook, NY, USA, 2019.
17. P. I. Pavlik, H. Cen, and K. R. Koedinger. Performance Factors Analysis – A New Alternative to Knowledge Tracing. Technical report, 2009. Publication Title: Online Submission ERIC Number: ED506305.
18. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot, and E. Duchesnay. Scikit-learn: Machine learning in Python. Journal of Machine Learning Research, 12:2825–2830, 2011.
19. C. Piech, J. Bassen, J. Huang, S. Ganguli, M. Sahami, L. J. Guibas, and J. Sohl-Dickstein. Deep Knowledge Tracing. In Advances in Neural Information Processing Systems, volume 28. Curran Associates, Inc., 2015.
20. T. S. Popkewitz. Educational Standards: Mapping Who We Are and Are to Become. Journal of the Learning Sciences, 13(2):243–256, Apr. 2004.
21. S. Ritter, J. R. Anderson, K. R. Koedinger, and A. Corbett. Cognitive Tutor: Applied research in mathematics education. Psychonomic Bulletin & Review, 14(2):249–255, Apr. 2007.
22. S. Shen, Q. Liu, Z. Huang, Y. Zheng, M. Yin, M. Wang, and E. Chen. A Survey of Knowledge Tracing: Models, Variants, and Applications. IEEE Transactions on Learning Technologies, 17:1898–1919, 2024. Conference Name: IEEE Transactions on Learning Technologies.
23. J.-J. Vie and H. Kashima. Knowledge Tracing Machines: Factorization Machines for Knowledge Tracing. Proceedings of the AAAI Conference on Artificial Intelligence, 33(01):750–757, July 2019. Number: 01.
24. X. Wang, Z. Wang, W. Shao, C. Jia, and X. Li. Explaining Concept Drift of Deep Learning Models. In J. Vaidya, X. Zhang, and J. Li, editors, Cyberspace Safety and Security, pages 524–534, Cham, 2019. Springer International Publishing.
25. C.-K. Yeung. Deep-IRT: Make Deep Learning Based Knowledge Tracing Explainable Using Item Response Theory, Apr. 2019. arXiv:1904.11738.

© 2025 Copyright is held by the author(s). This work is distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) license.